Quasi-analytic function
Encyclopedia
In mathematics, a quasi-analytic class of functions is a generalization of the class of real analytic function
s based upon the following fact. If f is an analytic function on an interval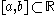
, and at some point f and all of its derivatives are zero, then f is identically zero on all of 
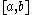. Quasi-analytic classes are broader classes of functions for which this statement still holds true.
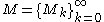be a sequence of positive real numbers with 
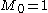. Then we define the class of functions 
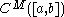to be those 
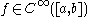which satisfy
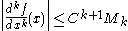
for all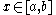
, some constant C, and all non-negative integers k. If 
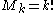this is exactly the class of real analytic function
s on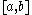
. The class 
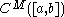is said to be quasi-analytic if whenever 
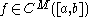and
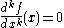
for some point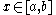
and all k, f is identically equal to zero.
A function f is called a quasi-analytic function if f is in some quasi-analytic class.
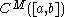is a quasi-analytic class. It states that the following conditions are equivalent:
The proof that the last two conditions are equivalent to the second uses Carleman's inequality
.
Example: pointed out that if Mn is given by one of the sequences
, 
, 
, 
, …
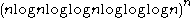then the corresponding class is quasi-analytic. The first sequence gives analytic functions.
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
s based upon the following fact. If f is an analytic function on an interval
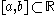, and at some point f and all of its derivatives are zero, then f is identically zero on all of 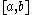. Quasi-analytic classes are broader classes of functions for which this statement still holds true.Definitions
Let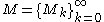 be a sequence of positive real numbers with 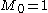. Then we define the class of functions 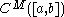to be those 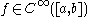which satisfy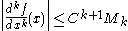for all
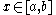, some constant C, and all non-negative integers k. If 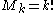this is exactly the class of real analytic functionAnalytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
s on
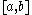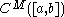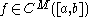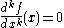
. The class is said to be quasi-analytic if whenever andfor some point
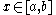and all k, f is identically equal to zero.A function f is called a quasi-analytic function if f is in some quasi-analytic class.
The Denjoy–Carleman theorem
The Denjoy–Carleman theorem, proved by after gave some partial results, gives criteria on the sequence M under which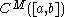 is a quasi-analytic class. It states that the following conditions are equivalent:
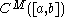is quasi-analytic
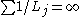where 
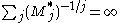, where Mj* is the largest log convex sequence bounded above by Mj.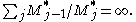
The proof that the last two conditions are equivalent to the second uses Carleman's inequality
Carleman's inequality
Carleman's inequality is an inequality in mathematics, named after Torsten Carleman, who proved it in 1923 and used it to prove Carleman's condition for the determinancy of the problem of moments.-Statement:Let a1, a2, a3, .....
.
Example: pointed out that if Mn is given by one of the sequences
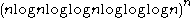, , , , …then the corresponding class is quasi-analytic. The first sequence gives analytic functions.