Young's modulus
Encyclopedia
Young's modulus is a measure of the stiffness
of an elastic material and is a quantity used to characterize materials. It is defined as the ratio of the uniaxial stress
over the uniaxial strain
in the range of stress in which Hooke's Law
holds. In solid mechanics
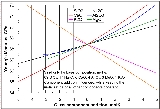
, the slope of the stress-strain curve
at any point is called the tangent modulus
. The tangent modulus of the initial, linear portion of a stress-strain curve is called Young's modulus, also known as the tensile modulus. It can be experimentally determined from the slope
of a stress-strain curve
created during tensile tests conducted on a sample of the material. In anisotropic materials, Young's modulus may have different values depending on the direction of the applied force with respect to the material's structure.
It is also commonly called the elastic modulus
or modulus of elasticity, because Young's modulus is the most common elastic modulus used, but there are other elastic moduli measured, too, such as the bulk modulus
and the shear modulus.
Young's modulus is named after Thomas Young
, the 19th century British scientist. However, the concept was developed in 1727 by Leonhard Euler
, and the first experiments that used the concept of Young's modulus in its current form were performed by the Italian scientist Giordano Riccati
in 1782, predating Young's work by 25 years.
, which has units of pressure
, to strain
, which is dimensionless
; therefore, Young's modulus has units of pressure
.
The SI
unit of modulus of elasticity (E, or less commonly Y) is the pascal
(Pa or N/m² or m−1·kg·s−2). The practical units used are megapascals (MPa or N/mm²) or gigapascals (GPa or kN/mm²). In United States customary units
, it is expressed as pounds (force) per square inch
(psi).
, or Poisson's ratio
. It also helps in selection of materials for particular structural applications.
. Examples of linear materials are steel
, carbon fiber and glass
. Non-linear materials include rubber
and soils, except under very small strains.
, and their mechanical properties are the same in all orientations. However, metals and ceramics can be treated with certain impurities, and metals can be mechanically worked to make their grain structures directional. These materials then become anisotropic
, and Young's modulus will change depending on the direction from which the force is applied. Anisotropy can be seen in many composites as well. For example, carbon fiber has much higher Young's modulus (is much stiffer) when force is loaded parallel to the fibers (along the grain). Other such materials include wood
and reinforced concrete
. Engineers can use this directional phenomenon to their advantage in creating structures.
by the tensile strain in the elastic (initial, linear) portion of the stress-strain curve
:
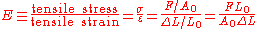
where
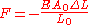
where F is the force exerted by the material when compressed or stretched by ΔL.
Hooke's law
can be derived from this formula, which describes the stiffness of an ideal spring: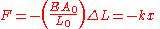
where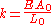
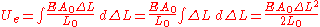
where Ue is the elastic potential energy.
The elastic potential energy per unit volume is given by: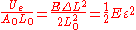
, where 
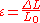is the strain in the material.
This formula can also be expressed as the integral of Hooke's law:
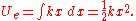
exist between elastic constants (Young's modulus E, shear modulus G, bulk modulus
K, and Poisson's ratio
ν) that allow calculating them all as long as two are known:
Young's modulus can vary somewhat due to differences in sample composition and test method. The rate of deformation has the greatest impact on the data collected, especially in polymers. The values here are approximate and only meant for relative comparison.
Stiffness
Stiffness is the resistance of an elastic body to deformation by an applied force along a given degree of freedom when a set of loading points and boundary conditions are prescribed on the elastic body.-Calculations:...
of an elastic material and is a quantity used to characterize materials. It is defined as the ratio of the uniaxial stress
Stress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
over the uniaxial strain
Strain (materials science)
In continuum mechanics, the infinitesimal strain theory, sometimes called small deformation theory, small displacement theory, or small displacement-gradient theory, deals with infinitesimal deformations of a continuum body...
in the range of stress in which Hooke's Law
Hooke's law
In mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...
holds. In solid mechanics
Solid mechanics
Solid mechanics is the branch of mechanics, physics, and mathematics that concerns the behavior of solid matter under external actions . It is part of a broader study known as continuum mechanics. One of the most common practical applications of solid mechanics is the Euler-Bernoulli beam equation...
, the slope of the stress-strain curve
Stress-strain curve
During tensile testing of a material sample, the stress–strain curve is a graphical representation of the relationship between stress, derived from measuring the load applied on the sample, and strain, derived from measuring the deformation of the sample, i.e. elongation, compression, or distortion...
at any point is called the tangent modulus
Tangent modulus
In solid mechanics, the tangent modulus is the slope of the compression stress-strain curve at any specified stress or strain. Below the proportional limit the tangent modulus is equivalent to Young's modulus. Above the proportional limit the tangent modulus varies with strain and is most...
. The tangent modulus of the initial, linear portion of a stress-strain curve is called Young's modulus, also known as the tensile modulus. It can be experimentally determined from the slope
Slope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
of a stress-strain curve
Stress-strain curve
During tensile testing of a material sample, the stress–strain curve is a graphical representation of the relationship between stress, derived from measuring the load applied on the sample, and strain, derived from measuring the deformation of the sample, i.e. elongation, compression, or distortion...
created during tensile tests conducted on a sample of the material. In anisotropic materials, Young's modulus may have different values depending on the direction of the applied force with respect to the material's structure.
It is also commonly called the elastic modulus
Elastic modulus
An elastic modulus, or modulus of elasticity, is the mathematical description of an object or substance's tendency to be deformed elastically when a force is applied to it...
or modulus of elasticity, because Young's modulus is the most common elastic modulus used, but there are other elastic moduli measured, too, such as the bulk modulus
Bulk modulus
The bulk modulus of a substance measures the substance's resistance to uniform compression. It is defined as the pressure increase needed to decrease the volume by a factor of 1/e...
and the shear modulus.
Young's modulus is named after Thomas Young
Thomas Young (scientist)
Thomas Young was an English polymath. He is famous for having partly deciphered Egyptian hieroglyphics before Jean-François Champollion eventually expanded on his work...
, the 19th century British scientist. However, the concept was developed in 1727 by Leonhard Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
, and the first experiments that used the concept of Young's modulus in its current form were performed by the Italian scientist Giordano Riccati
Giordano Riccati
Giordano Riccati or Jordan Riccati was the first experimental mechanician to study material elastic moduli as we understand them today. His 1782 paper on determining the relative Young's moduli of steel and brass using flexural vibrations predated Thomas Young's 1807 paper on the subject of moduli...
in 1782, predating Young's work by 25 years.
Units
Young's modulus is the ratio of stressStress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
, which has units of pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
, to strain
Strain (materials science)
In continuum mechanics, the infinitesimal strain theory, sometimes called small deformation theory, small displacement theory, or small displacement-gradient theory, deals with infinitesimal deformations of a continuum body...
, which is dimensionless
Dimensionless quantity
In dimensional analysis, a dimensionless quantity or quantity of dimension one is a quantity without an associated physical dimension. It is thus a "pure" number, and as such always has a dimension of 1. Dimensionless quantities are widely used in mathematics, physics, engineering, economics, and...
; therefore, Young's modulus has units of pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
.
The SI
Si
Si, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
unit of modulus of elasticity (E, or less commonly Y) is the pascal
Pascal (unit)
The pascal is the SI derived unit of pressure, internal pressure, stress, Young's modulus and tensile strength, named after the French mathematician, physicist, inventor, writer, and philosopher Blaise Pascal. It is a measure of force per unit area, defined as one newton per square metre...
(Pa or N/m² or m−1·kg·s−2). The practical units used are megapascals (MPa or N/mm²) or gigapascals (GPa or kN/mm²). In United States customary units
United States customary units
United States customary units are a system of measurements commonly used in the United States. Many U.S. units are virtually identical to their imperial counterparts, but the U.S. customary system developed from English units used in the British Empire before the system of imperial units was...
, it is expressed as pounds (force) per square inch
Pounds per square inch
The pound per square inch or, more accurately, pound-force per square inch is a unit of pressure or of stress based on avoirdupois units...
(psi).
Usage
The Young's modulus calculates the change in the dimension of a bar made of an isotropic elastic material under tensile or compressive loads. For instance, it predicts how much a material sample extends under tension or shortens under compression. Some calculations also require the use of other material properties, such as the shear modulus, densityDensity
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
, or Poisson's ratio
Poisson's ratio
Poisson's ratio , named after Siméon Poisson, is the ratio, when a sample object is stretched, of the contraction or transverse strain , to the extension or axial strain ....
. It also helps in selection of materials for particular structural applications.
Linear versus non-linear
For many materials, Young's modulus is essentially constant over a range of strains. Such materials are called linear, and are said to obey Hooke's lawHooke's law
In mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...
. Examples of linear materials are steel
Steel
Steel is an alloy that consists mostly of iron and has a carbon content between 0.2% and 2.1% by weight, depending on the grade. Carbon is the most common alloying material for iron, but various other alloying elements are used, such as manganese, chromium, vanadium, and tungsten...
, carbon fiber and glass
Glass
Glass is an amorphous solid material. Glasses are typically brittle and optically transparent.The most familiar type of glass, used for centuries in windows and drinking vessels, is soda-lime glass, composed of about 75% silica plus Na2O, CaO, and several minor additives...
. Non-linear materials include rubber
Rubber
Natural rubber, also called India rubber or caoutchouc, is an elastomer that was originally derived from latex, a milky colloid produced by some plants. The plants would be ‘tapped’, that is, an incision made into the bark of the tree and the sticky, milk colored latex sap collected and refined...
and soils, except under very small strains.
Directional materials
Young's modulus is not always the same in all orientations of a material. Most metals and ceramics, along with many other materials, are isotropicIsotropy
Isotropy is uniformity in all orientations; it is derived from the Greek iso and tropos . Precise definitions depend on the subject area. Exceptions, or inequalities, are frequently indicated by the prefix an, hence anisotropy. Anisotropy is also used to describe situations where properties vary...
, and their mechanical properties are the same in all orientations. However, metals and ceramics can be treated with certain impurities, and metals can be mechanically worked to make their grain structures directional. These materials then become anisotropic
Anisotropy
Anisotropy is the property of being directionally dependent, as opposed to isotropy, which implies identical properties in all directions. It can be defined as a difference, when measured along different axes, in a material's physical or mechanical properties An example of anisotropy is the light...
, and Young's modulus will change depending on the direction from which the force is applied. Anisotropy can be seen in many composites as well. For example, carbon fiber has much higher Young's modulus (is much stiffer) when force is loaded parallel to the fibers (along the grain). Other such materials include wood
Wood
Wood is a hard, fibrous tissue found in many trees. It has been used for hundreds of thousands of years for both fuel and as a construction material. It is an organic material, a natural composite of cellulose fibers embedded in a matrix of lignin which resists compression...
and reinforced concrete
Reinforced concrete
Reinforced concrete is concrete in which reinforcement bars , reinforcement grids, plates or fibers have been incorporated to strengthen the concrete in tension. It was invented by French gardener Joseph Monier in 1849 and patented in 1867. The term Ferro Concrete refers only to concrete that is...
. Engineers can use this directional phenomenon to their advantage in creating structures.
Calculation
Young's modulus, E, can be calculated by dividing the tensile stressStress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
by the tensile strain in the elastic (initial, linear) portion of the stress-strain curve
Stress-strain curve
During tensile testing of a material sample, the stress–strain curve is a graphical representation of the relationship between stress, derived from measuring the load applied on the sample, and strain, derived from measuring the deformation of the sample, i.e. elongation, compression, or distortion...
:
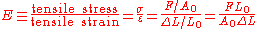
where
- E is the Young's modulus (modulus of elasticity)
- F is the force exerted on an object under tension;
- A0 is the original cross-sectional area through which the force is applied;
- ΔL is the amount by which the length of the object changes;
- L0 is the original length of the object.
Force exerted by stretched or compressed material
The Young's modulus of a material can be used to calculate the force it exerts under specific strain.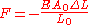where F is the force exerted by the material when compressed or stretched by ΔL.
Hooke's law
Hooke's law
In mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...
can be derived from this formula, which describes the stiffness of an ideal spring:
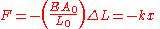
where
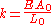
Elastic potential energy
The elastic potential energy stored is given by the integral of this expression with respect to L: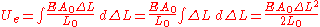where Ue is the elastic potential energy.
The elastic potential energy per unit volume is given by:
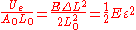, where 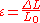is the strain in the material.This formula can also be expressed as the integral of Hooke's law:
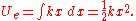
Relation among elastic constants
For homogeneous isotropic materials simple relationsElastic modulus
An elastic modulus, or modulus of elasticity, is the mathematical description of an object or substance's tendency to be deformed elastically when a force is applied to it...
exist between elastic constants (Young's modulus E, shear modulus G, bulk modulus
Bulk modulus
The bulk modulus of a substance measures the substance's resistance to uniform compression. It is defined as the pressure increase needed to decrease the volume by a factor of 1/e...
K, and Poisson's ratio
Poisson's ratio
Poisson's ratio , named after Siméon Poisson, is the ratio, when a sample object is stretched, of the contraction or transverse strain , to the extension or axial strain ....
ν) that allow calculating them all as long as two are known:
Approximate values
| Material | GPa Pascal (unit) The pascal is the SI derived unit of pressure, internal pressure, stress, Young's modulus and tensile strength, named after the French mathematician, physicist, inventor, writer, and philosopher Blaise Pascal. It is a measure of force per unit area, defined as one newton per square metre... |
lbf/in² (psi) |
|---|---|---|
| Rubber Rubber Natural rubber, also called India rubber or caoutchouc, is an elastomer that was originally derived from latex, a milky colloid produced by some plants. The plants would be ‘tapped’, that is, an incision made into the bark of the tree and the sticky, milk colored latex sap collected and refined... (small strain) |
0.01–0.1 | 1,500–15,000 |
| PTFE (Teflon) | 0.5 | 75,000 |
| Low density polyethylene Low density polyethylene Low-density polyethylene is a thermoplastic made from petroleum. It was the first grade of polyethylene, produced in 1933 by Imperial Chemical Industries using a high pressure process via free radical polymerization. Its manufacture employs the same method today. LDPE is commonly recycled and has... |
0.2 | 30,000 |
| HDPE | 0.8 | |
| Polypropylene Polypropylene Polypropylene , also known as polypropene, is a thermoplastic polymer used in a wide variety of applications including packaging, textiles , stationery, plastic parts and reusable containers of various types, laboratory equipment, loudspeakers, automotive components, and polymer banknotes... |
1.5-2 | 217,000–290,000 |
| Bacteriophage capsids Capsid A capsid is the protein shell of a virus. It consists of several oligomeric structural subunits made of protein called protomers. The observable 3-dimensional morphological subunits, which may or may not correspond to individual proteins, are called capsomeres. The capsid encloses the genetic... |
1–3 | 150,000–435,000 |
| Polyethylene terephthalate Polyethylene terephthalate Polyethylene terephthalate , commonly abbreviated PET, PETE, or the obsolete PETP or PET-P, is a thermoplastic polymer resin of the polyester family and is used in synthetic fibers; beverage, food and other liquid containers; thermoforming applications; and engineering resins often in combination... |
2-2.7 | |
| Polystyrene Polystyrene Polystyrene ) also known as Thermocole, abbreviated following ISO Standard PS, is an aromatic polymer made from the monomer styrene, a liquid hydrocarbon that is manufactured from petroleum by the chemical industry... |
3-3.5 | 435,000–505,000 |
| Nylon Nylon Nylon is a generic designation for a family of synthetic polymers known generically as polyamides, first produced on February 28, 1935, by Wallace Carothers at DuPont's research facility at the DuPont Experimental Station... |
2–4 | 290,000–580,000 |
| Diatom Diatom Diatoms are a major group of algae, and are one of the most common types of phytoplankton. Most diatoms are unicellular, although they can exist as colonies in the shape of filaments or ribbons , fans , zigzags , or stellate colonies . Diatoms are producers within the food chain... frustules (largely silicic acid Silicic acid Silicic acid is a general name for a family of chemical compounds of the element silicon, hydrogen, and oxygen, with the general formula [SiOx4-2x]n... ) |
0.35–2.77 | 50,000–400,000 |
| Medium-density fiberboard | 4 | 580,000 |
| Pine wood Wood Wood is a hard, fibrous tissue found in many trees. It has been used for hundreds of thousands of years for both fuel and as a construction material. It is an organic material, a natural composite of cellulose fibers embedded in a matrix of lignin which resists compression... (along grain) |
9 | 1,300,000 |
| Oak wood Wood Wood is a hard, fibrous tissue found in many trees. It has been used for hundreds of thousands of years for both fuel and as a construction material. It is an organic material, a natural composite of cellulose fibers embedded in a matrix of lignin which resists compression... (along grain) |
11 | 1,600,000 |
| High-strength concrete Concrete Concrete is a composite construction material, composed of cement and other cementitious materials such as fly ash and slag cement, aggregate , water and chemical admixtures.The word concrete comes from the Latin word... (under compression) |
30 | 4,350,000 |
| Hemp Hemp Hemp is mostly used as a name for low tetrahydrocannabinol strains of the plant Cannabis sativa, of fiber and/or oilseed varieties. In modern times, hemp has been used for industrial purposes including paper, textiles, biodegradable plastics, construction, health food and fuel with modest... fiber |
35 | |
| Magnesium Magnesium Magnesium is a chemical element with the symbol Mg, atomic number 12, and common oxidation number +2. It is an alkaline earth metal and the eighth most abundant element in the Earth's crust and ninth in the known universe as a whole... metal Metal A metal , is an element, compound, or alloy that is a good conductor of both electricity and heat. Metals are usually malleable and shiny, that is they reflect most of incident light... (Mg) |
45 | 6,500,000 |
| Flax Flax Flax is a member of the genus Linum in the family Linaceae. It is native to the region extending from the eastern Mediterranean to India and was probably first domesticated in the Fertile Crescent... fiber |
58 | |
| Aluminium Aluminium Aluminium or aluminum is a silvery white member of the boron group of chemical elements. It has the symbol Al, and its atomic number is 13. It is not soluble in water under normal circumstances.... |
69 | 10,000,000 |
| Stinging nettle Stinging nettle Stinging nettle or common nettle, Urtica dioica, is a herbaceous perennial flowering plant, native to Europe, Asia, northern Africa, and North America, and is the best-known member of the nettle genus Urtica... fiber |
87 | |
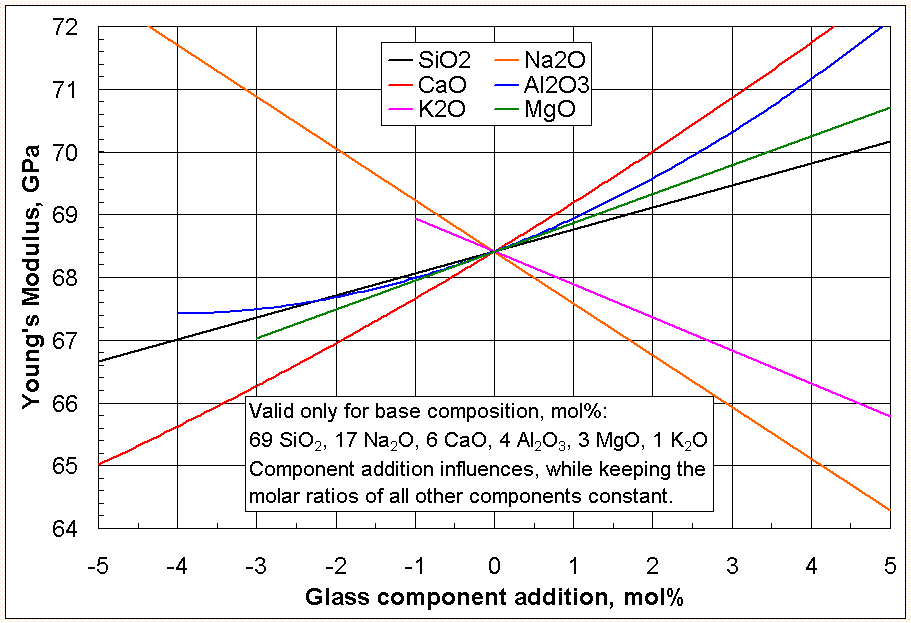
| Glass Glass Glass is an amorphous solid material. Glasses are typically brittle and optically transparent.The most familiar type of glass, used for centuries in windows and drinking vessels, is soda-lime glass, composed of about 75% silica plus Na2O, CaO, and several minor additives... (see chart) |
50–90 | |
| Aramid Aramid Aramid fibers are a class of heat-resistant and strong synthetic fibers. They are used in aerospace and military applications, for ballistic rated body armor fabric and ballistic composites, in bicycle tires, and as an asbestos substitute. The name is a portmanteau of "aromatic polyamide"... |
70.5–112.4 | |
| Mother-of-pearl (nacre Nacre Nacre , also known as mother of pearl, is an organic-inorganic composite material produced by some mollusks as an inner shell layer; it is also what makes up pearls. It is very strong, resilient, and iridescent.... , largely calcium carbonate) |
70 | 10,000,000 |
| Tooth enamel Tooth enamel Tooth enamel, along with dentin, cementum, and dental pulp is one of the four major tissues that make up the tooth in vertebrates. It is the hardest and most highly mineralized substance in the human body. Tooth enamel is also found in the dermal denticles of sharks... (largely calcium phosphate Calcium phosphate Calcium phosphate is the name given to a family of minerals containing calcium ions together with orthophosphates , metaphosphates or pyrophosphates and occasionally hydrogen or hydroxide ions .... ) |
83 | 12,000,000 |
| Brass Brass Brass is an alloy of copper and zinc; the proportions of zinc and copper can be varied to create a range of brasses with varying properties.In comparison, bronze is principally an alloy of copper and tin... and bronze Bronze Bronze is a metal alloy consisting primarily of copper, usually with tin as the main additive. It is hard and brittle, and it was particularly significant in antiquity, so much so that the Bronze Age was named after the metal... |
100–125 | 17,000,000 |
| Titanium Titanium Titanium is a chemical element with the symbol Ti and atomic number 22. It has a low density and is a strong, lustrous, corrosion-resistant transition metal with a silver color.... (Ti) |
16,000,000 | |
| Titanium alloy Titanium alloy Titanium alloys are metallic materials which contain a mixture of titanium and other chemical elements. Such alloys have very high tensile strength and toughness , light weight, extraordinary corrosion resistance, and ability to withstand extreme temperatures... s |
105–120 | 15,000,000–17,500,000 |
| Copper Copper Copper is a chemical element with the symbol Cu and atomic number 29. It is a ductile metal with very high thermal and electrical conductivity. Pure copper is soft and malleable; an exposed surface has a reddish-orange tarnish... (Cu) |
117 | 17,000,000 |
| Glass-reinforced plastic Glass-reinforced plastic Fiberglass , is a fiber reinforced polymer made of a plastic matrix reinforced by fine fibers of glass. It is also known as GFK .... (70/30 by weight fibre/matrix, unidirectional, along grain) |
40–45 | 5,800,000–6,500,000 |
| Glass-reinforced polyester matrix Glass-reinforced plastic Fiberglass , is a fiber reinforced polymer made of a plastic matrix reinforced by fine fibers of glass. It is also known as GFK .... |
17.2 | 2,500,000 |
| Carbon fiber reinforced plastic (50/50 fibre/matrix, unidirectional, along grain) | 125–150 | 18,000,000–22,000,000 |
| Carbon fiber reinforced plastic (70/30 fibre/matrix, unidirectional, along grain) | 181 | 26,300,000 |
| Silicon Silicon Silicon is a chemical element with the symbol Si and atomic number 14. A tetravalent metalloid, it is less reactive than its chemical analog carbon, the nonmetal directly above it in the periodic table, but more reactive than germanium, the metalloid directly below it in the table... single crystal, different directions |
130-185 | |
| Wrought iron Wrought iron thumb|The [[Eiffel tower]] is constructed from [[puddle iron]], a form of wrought ironWrought iron is an iron alloy with a very low carbon... |
190–210 | |
| Steel Steel Steel is an alloy that consists mostly of iron and has a carbon content between 0.2% and 2.1% by weight, depending on the grade. Carbon is the most common alloying material for iron, but various other alloying elements are used, such as manganese, chromium, vanadium, and tungsten... |
200 | 29,000,000 |
| polycrystalline Yttrium iron garnet Yttrium iron garnet Yttrium iron garnet is a kind of synthetic garnet, with chemical composition 323, or Y3Fe5O12. It is a ferrimagnetic material with a Curie temperature of 550 K.... (YIG) |
193 | 28,000,000 |
| single-crystal Yttrium iron garnet Yttrium iron garnet Yttrium iron garnet is a kind of synthetic garnet, with chemical composition 323, or Y3Fe5O12. It is a ferrimagnetic material with a Curie temperature of 550 K.... (YIG) |
200 | 30,000,000 |
| Beryllium Beryllium Beryllium is the chemical element with the symbol Be and atomic number 4. It is a divalent element which occurs naturally only in combination with other elements in minerals. Notable gemstones which contain beryllium include beryl and chrysoberyl... (Be) |
287 | 42,000,000 |
| Molybdenum Molybdenum Molybdenum , is a Group 6 chemical element with the symbol Mo and atomic number 42. The name is from Neo-Latin Molybdaenum, from Ancient Greek , meaning lead, itself proposed as a loanword from Anatolian Luvian and Lydian languages, since its ores were confused with lead ores... (Mo) |
329 | |
| Tungsten Tungsten Tungsten , also known as wolfram , is a chemical element with the chemical symbol W and atomic number 74.A hard, rare metal under standard conditions when uncombined, tungsten is found naturally on Earth only in chemical compounds. It was identified as a new element in 1781, and first isolated as... (W) |
400–410 | 58,000,000–59,500,000 |
| Sapphire Sapphire Sapphire is a gemstone variety of the mineral corundum, an aluminium oxide , when it is a color other than red or dark pink; in which case the gem would instead be called a ruby, considered to be a different gemstone. Trace amounts of other elements such as iron, titanium, or chromium can give... (Al2O3) along C-axis |
435 | 63,000,000 |
| Silicon carbide Silicon carbide Silicon carbide , also known as carborundum, is a compound of silicon and carbon with chemical formula SiC. It occurs in nature as the extremely rare mineral moissanite. Silicon carbide powder has been mass-produced since 1893 for use as an abrasive... (SiC) |
450 | 65,000,000 |
| Osmium Osmium Osmium is a chemical element with the symbol Os and atomic number 76. Osmium is a hard, brittle, blue-gray or blue-blacktransition metal in the platinum family, and is the densest natural element. Osmium is twice as dense as lead. The density of osmium is , slightly greater than that of iridium,... (Os) |
550 | 79,800,000 |
| Tungsten carbide Tungsten carbide Tungsten carbide is an inorganic chemical compound containing equal parts of tungsten and carbon atoms. Colloquially, tungsten carbide is often simply called carbide. In its most basic form, it is a fine gray powder, but it can be pressed and formed into shapes for use in industrial machinery,... (WC) |
450–650 | 65,000,000–94,000,000 |
| Single-walled carbon nanotube | 1,000+ | 145,000,000+ |
| Graphene Graphene Graphene is an allotrope of carbon, whose structure is one-atom-thick planar sheets of sp2-bonded carbon atoms that are densely packed in a honeycomb crystal lattice. The term graphene was coined as a combination of graphite and the suffix -ene by Hanns-Peter Boehm, who described single-layer... |
1000 | |
| Diamond Diamond In mineralogy, diamond is an allotrope of carbon, where the carbon atoms are arranged in a variation of the face-centered cubic crystal structure called a diamond lattice. Diamond is less stable than graphite, but the conversion rate from diamond to graphite is negligible at ambient conditions... (C) |
1220 | 150,000,000–175,000,000 |
See also
- DeflectionDeflection (engineering)In engineering, deflection is the degree to which a structural element is displaced under a load. It may refer to an angle or a distance.The deflection distance of a member under a load is directly related to the slope of the deflected shape of the member under that load and can be calculated by...
- Deformation
- Hardness
- Hooke's lawHooke's lawIn mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...
- Shear modulus
- Bending stiffnessBending stiffnessThe bending stiffness E I of a beam relates the applied bending moment to the resulting deflection of the beam. It is the product of the elastic modulus E of the beam material and the area moment of inertia I of the beam cross-section...
- Impulse excitation techniqueImpulse excitation technique-Practical:The impulse excitation technique is a nondestructive test method that uses natural frequency, dimensions and mass of a test-piece to determine Young's modulus, Shear modulus, Poisson's ratio and damping coefficient....
- ToughnessToughnessIn materials science and metallurgy, toughness is the ability of a material to absorb energy and plastically deform without fracturing; Material toughness is defined as the amount of energy per volume that a material can absorb before rupturing...
- Yield (engineering)Yield (engineering)The yield strength or yield point of a material is defined in engineering and materials science as the stress at which a material begins to deform plastically. Prior to the yield point the material will deform elastically and will return to its original shape when the applied stress is removed...
- List of materials properties