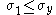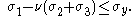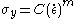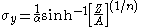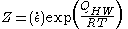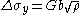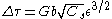.gif)
Yield (engineering)
Encyclopedia
The yield strength or yield point of a material
is defined in engineering
and materials science
as the stress
at which a material begins to deform plastically
. Prior to the yield point the material will deform elastically
and will return to its original shape when the applied stress is removed. Once the yield point is passed, some fraction of the deformation will be permanent and non-reversible.
In the three-dimensional space of the principal stresses (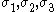
), an infinite number of yield points form together a yield surface
.
Knowledge of the yield point is vital when designing a component since it generally represents an upper limit to the load that can be applied. It is also important for the control of many materials production techniques such as forging
, rolling
, or pressing
. In structural engineering, this is a soft failure mode which does not normally cause catastrophic failure
or ultimate failure
unless it accelerates buckling
.
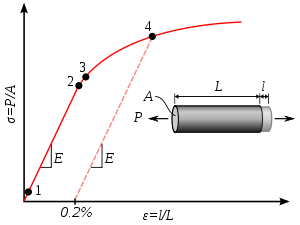It is often difficult to precisely define yielding due to the wide variety of stress–strain curves exhibited by real materials. In addition, there are several possible ways to define yielding:
True elastic limit
Proportionality limit
Elastic limit (yield strength)
Yield point : The point in the stress-strain curve at which the curve levels off and plastic deformation begins to occur.
Offset yield point : When a yield point is not easily defined based on the shape of the stress-strain curve an offset yield point is arbitrarily defined. The value for this is commonly set at 0.1 or 0.2% of the strain. The offset value is given as a subscript, e.g., Rp0.2=310 MPa. High strength steel and aluminum alloys do not exhibit a yield point, so this offset yield point is used on these materials.
Upper yield point and lower yield point
qualities they can be described on the basis of three principal directions, in the case of stress these are denoted by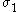
, 
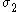, and 
.
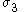The following represent the most common yield criterion as applied to an isotropic material (uniform properties in all directions). Other equations have been proposed or are used in specialist situations.
Maximum Principal Strain Theory - Yield occurs when the maximum principal strain
reaches the strain corresponding to the yield point during a simple tensile test. In terms of the principal stresses this is determined by the equation:
Maximum Shear Stress Theory - Also known as the Tresca yield criterion, after the French scientist Henri Tresca
. This assumes that yield occurs when the shear stress
exceeds the shear yield strength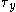 
:
Total Strain Energy Theory - This theory assumes that the stored energy associated with elastic deformation at the point of yield is independent of the specific stress tensor. Thus yield occurs when the strain energy per unit volume is greater than the strain energy at the elastic limit in simple tension. For a 3-dimensional stress state this is given by:
Distortion Energy Theory - This theory proposes that the total strain energy can be separated into two components: the volumetric (hydrostatic) strain energy and the shape (distortion or shear
) strain energy. It is proposed that yield occurs when the distortion component exceeds that at the yield point for a simple tensile test. This is generally referred to as the Von Mises yield criterion and is expressed as:
Based on a different theoretical underpinning this expression is also referred to as octahedral shear stress theory.
Other commonly used isotropic yield criteria are the
The yield surface
s corresponding to these criteria have a range of forms. However, most isotropic yield criteria correspond to convex
yield surfaces.
Some of the more popular anisotropic yield criteria are:
where C is a constant and m is the strain rate sensitivity. The latter generally increases with temperature, and materials where m reaches a value greater than ~0.5 tend to exhibit super plastic behaviour.
Later, more complex equations were proposed that simultaneously dealt with both temperature and strain rate:
where α and A are constants and Z is the temperature-compensated strain-rate - often described by the Zener-Hollomon parameter:
where QHW is the activation energy for hot deformation and T is the absolute temperature.
These mechanisms for crystalline materials include
Work Hardening
Where deforming the material will introduce dislocation
s, which increases their density in the material. This increases the yield strength of the material, since now more stress must be applied to move these dislocations through a crystal lattice. Dislocations can also interact with each other, becoming entangled.
The governing formula for this mechanism is:
where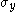
is the yield stress, G is the shear elastic modulus, b is the magnitude of the Burgers vector
, and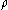
is the dislocation density.
Solid Solution Strengthening
By alloy
ing the material, impurity atoms in low concentrations will occupy a lattice position directly below a dislocation, such as directly below an extra half plane defect. This relieves a tensile strain directly below the dislocation by filling that empty lattice space with the impurity atom.
The relationship of this mechanism goes as:
where
is the shear stress
, related to the yield stress, G and b are the same as in the above example, C_s is the concentration of solute and
is the strain induced in the lattice due to adding the impurity.
Particle/Precipitate Strengthening
Where the presence of a secondary phase will increase yield strength by blocking the motion of dislocations within the crystal. A line defect that, while moving through the matrix, will be forced against a small particle or precipitate of the material. Dislocations can move through this particle either by shearing the particle, or by a process known as bowing or ringing, in which a new ring of dislocations is created around the particle.
The shearing formula goes as:
and the bowing/ringing formula:
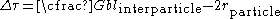
In these formulas,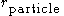
is the particle radius, 
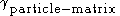is the surface tension between the matrix and the particle, 
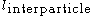is the distance between the particles.
Grain boundary strengthening
Where a buildup of dislocations at a grain boundary causes a repulsive force between dislocations. As grain size decreases, the surface area to volume ratio of the grain increases, allowing more buildup of dislocations at the grain edge. Since it requires a lot of energy to move dislocations to another grain, these dislocations build up along the boundary, and increase the yield stress of the material. Also known as Hall-Petch strengthening, this type of strengthening is governed by the formula:
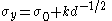
where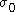
is the stress required to move dislocations,
Indentation hardness
correlates linearly with tensile strength for most steels. Hardness testing can therefore be an economical substitute for tensile testing, as well as providing local variations in yield strength due to e.g. welding or forming operations.
Material
Material is anything made of matter, constituted of one or more substances. Wood, cement, hydrogen, air and water are all examples of materials. Sometimes the term "material" is used more narrowly to refer to substances or components with certain physical properties that are used as inputs to...
is defined in engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
and materials science
Materials science
Materials science is an interdisciplinary field applying the properties of matter to various areas of science and engineering. This scientific field investigates the relationship between the structure of materials at atomic or molecular scales and their macroscopic properties. It incorporates...
as the stress
Stress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
at which a material begins to deform plastically
Plasticity (physics)
In physics and materials science, plasticity describes the deformation of a material undergoing non-reversible changes of shape in response to applied forces. For example, a solid piece of metal being bent or pounded into a new shape displays plasticity as permanent changes occur within the...
. Prior to the yield point the material will deform elastically
Elasticity (physics)
In physics, elasticity is the physical property of a material that returns to its original shape after the stress that made it deform or distort is removed. The relative amount of deformation is called the strain....
and will return to its original shape when the applied stress is removed. Once the yield point is passed, some fraction of the deformation will be permanent and non-reversible.
In the three-dimensional space of the principal stresses (
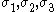), an infinite number of yield points form together a yield surfaceYield surface
A yield surface is a five-dimensional surface in the six-dimensional space of stresses. The yield surface is usually convex and the state of stress of inside the yield surface is elastic. When the stress state lies on the surface the material is said to have reached its yield point and the...
.
Knowledge of the yield point is vital when designing a component since it generally represents an upper limit to the load that can be applied. It is also important for the control of many materials production techniques such as forging
Forging
Forging is a manufacturing process involving the shaping of metal using localized compressive forces. Forging is often classified according to the temperature at which it is performed: '"cold," "warm," or "hot" forging. Forged parts can range in weight from less than a kilogram to 580 metric tons...
, rolling
Rolling (metalworking)
In metalworking, rolling is a metal forming process in which metal stock is passed through a pair of rolls. Rolling is classified according to the temperature of the metal rolled. If the temperature of the metal is above its recrystallization temperature, then the process is termed as hot rolling...
, or pressing
Machine press
A machine press, commonly shortened to press, is a machine tool that changes the shape of a workpiece.-Servomechanism:A servomechanism press, also known as a servo press or a electro press, is a press driven by an AC servo motor. The torque produced is converted to a linear force via a ball screw....
. In structural engineering, this is a soft failure mode which does not normally cause catastrophic failure
Catastrophic failure
A catastrophic failure is a sudden and total failure of some system from which recovery is impossible. Catastrophic failures often lead to cascading systems failure....
or ultimate failure
Ultimate failure
In mechanical engineering, ultimate failure describes the breaking of a material. In general there are two types of failure: fracture and buckling. Fracture of a material occurs when either an internal or external crack elongates the width or length of the material. In ultimate failure this will...
unless it accelerates buckling
Buckling
In science, buckling is a mathematical instability, leading to a failure mode.Theoretically, buckling is caused by a bifurcation in the solution to the equations of static equilibrium...
.
Definition
True elastic limit
- The lowest stress at which dislocationDislocationIn materials science, a dislocation is a crystallographic defect, or irregularity, within a crystal structure. The presence of dislocations strongly influences many of the properties of materials...
s move. This definition is rarely used, since dislocations move at very low stresses, and detecting such movement is very difficult.
Proportionality limit
- Up to this amount of stress, stress is proportional to strain (Hooke's lawHooke's lawIn mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...
), so the stress-strain graph is a straight line, and the gradient will be equal to the elastic modulusElastic modulusAn elastic modulus, or modulus of elasticity, is the mathematical description of an object or substance's tendency to be deformed elastically when a force is applied to it...
of the material.
Elastic limit (yield strength)
- Beyond the elastic limit, permanent deformation will occur. The lowest stress at which permanent deformation can be measured. This requires a manual load-unload procedure, and the accuracy is critically dependent on equipment and operator skill. For elastomerElastomerAn elastomer is a polymer with the property of viscoelasticity , generally having notably low Young's modulus and high yield strain compared with other materials. The term, which is derived from elastic polymer, is often used interchangeably with the term rubber, although the latter is preferred...
s, such as rubberRubberNatural rubber, also called India rubber or caoutchouc, is an elastomer that was originally derived from latex, a milky colloid produced by some plants. The plants would be ‘tapped’, that is, an incision made into the bark of the tree and the sticky, milk colored latex sap collected and refined...
, the elastic limit is much larger than the proportionality limit. Also, precise strain measurements have shown that plastic strain begins at low stresses.
Yield point : The point in the stress-strain curve at which the curve levels off and plastic deformation begins to occur.
Offset yield point : When a yield point is not easily defined based on the shape of the stress-strain curve an offset yield point is arbitrarily defined. The value for this is commonly set at 0.1 or 0.2% of the strain. The offset value is given as a subscript, e.g., Rp0.2=310 MPa. High strength steel and aluminum alloys do not exhibit a yield point, so this offset yield point is used on these materials.
Upper yield point and lower yield point
- Some metals, such as mild steel, reach an upper yield point before dropping rapidly to a lower yield point. The material response is linear up until the upper yield point, but the lower yield point is used in structural engineering as a conservative value. If a metal is only stressed to the upper yield point, and beyond, Lüders bands can develop.
Yield criterion
A yield criterion, often expressed as yield surface, or yield locus, is a hypothesis concerning the limit of elasticity under any combination of stresses. There are two interpretations of yield criterion: one is purely mathematical in taking a statistical approach while other models attempt to provide a justification based on established physical principles. Since stress and strain are tensorTensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
qualities they can be described on the basis of three principal directions, in the case of stress these are denoted by
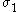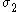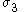, , and .The following represent the most common yield criterion as applied to an isotropic material (uniform properties in all directions). Other equations have been proposed or are used in specialist situations.
Isotropic yield criteria
Maximum Principal Stress Theory - Yield occurs when the largest principal stress exceeds the uniaxial tensile yield strength. Although this criterion allows for a quick and easy comparison with experimental data it is rarely suitable for design purposes.
Maximum Principal Strain Theory - Yield occurs when the maximum principal strain
Strain (materials science)
In continuum mechanics, the infinitesimal strain theory, sometimes called small deformation theory, small displacement theory, or small displacement-gradient theory, deals with infinitesimal deformations of a continuum body...
reaches the strain corresponding to the yield point during a simple tensile test. In terms of the principal stresses this is determined by the equation:
Maximum Shear Stress Theory - Also known as the Tresca yield criterion, after the French scientist Henri Tresca
Henri Tresca
Henri Édouard Tresca was a French mechanical engineer, and a professor at the Conservatoire National des Arts et Métiers in Paris....
. This assumes that yield occurs when the shear stress
exceeds the shear yield strength :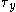
Total Strain Energy Theory - This theory assumes that the stored energy associated with elastic deformation at the point of yield is independent of the specific stress tensor. Thus yield occurs when the strain energy per unit volume is greater than the strain energy at the elastic limit in simple tension. For a 3-dimensional stress state this is given by:
Distortion Energy Theory - This theory proposes that the total strain energy can be separated into two components: the volumetric (hydrostatic) strain energy and the shape (distortion or shear
Shearing (physics)
Shearing in continuum mechanics refers to the occurrence of a shear strain, which is a deformation of a material substance in which parallel internal surfaces slide past one another. It is induced by a shear stress in the material...
) strain energy. It is proposed that yield occurs when the distortion component exceeds that at the yield point for a simple tensile test. This is generally referred to as the Von Mises yield criterion and is expressed as:
Based on a different theoretical underpinning this expression is also referred to as octahedral shear stress theory.
Other commonly used isotropic yield criteria are the
- Mohr-Coulomb yield criterionMohr-Coulomb theoryMohr–Coulomb theory is a mathematical model describing the response of brittle materials such as concrete, or rubble piles, to shear stress as well as normal stress. Most of the classical engineering materials somehow follow this rule in at least a portion of their shear failure envelope...
- Drucker-Prager yield criterion
- Bresler-Pister yield criterionBresler Pister yield criterionThe Bresler-Pister yield criterion is a function that was originally devised to predict the strength of concrete under multiaxial stress states...
- Willam-Warnke yield criterionWillam-Warnke yield criterionThe Willam-Warnke yield criterion is a function that is used to predict when failure will occur in concrete and other cohesive-frictional materials such as rock, soil, and ceramics...
The yield surface
Yield surface
A yield surface is a five-dimensional surface in the six-dimensional space of stresses. The yield surface is usually convex and the state of stress of inside the yield surface is elastic. When the stress state lies on the surface the material is said to have reached its yield point and the...
s corresponding to these criteria have a range of forms. However, most isotropic yield criteria correspond to convex
Convex
'The word convex means curving out or bulging outward, as opposed to concave. Convex or convexity may refer to:Mathematics:* Convex set, a set of points containing all line segments between each pair of its points...
yield surfaces.
Anisotropic yield criteria
When a metal is subjected to large plastic deformations the grain sizes and orientations change in the direction of deformation. As a result the plastic yield behavior of the material shows directional dependency. Under such circumstances, the isotropic yield criteria such as the von Mises yield criterion are unable to predict the yield behavior accurately. Several anisotropic yield criteria have been developed to deal with such situations.Some of the more popular anisotropic yield criteria are:
- Hill's quadratic yield criterionHill yield criteriaRodney Hill has developed several yield criteria for anisotropic plastic deformations. The earliest version was a straightforward extension of the von Mises yield criterion and had a quadratic form. This model was later generalized by allowing for an exponent m...
. - Generalized Hill yield criterionHill yield criteriaRodney Hill has developed several yield criteria for anisotropic plastic deformations. The earliest version was a straightforward extension of the von Mises yield criterion and had a quadratic form. This model was later generalized by allowing for an exponent m...
. - Hosford yield criterionHosford yield criterionThe Hosford yield criterion is a function that is used to determine whether a material has undergone plastic yielding under the action of stress.- Hosford yield criterion for isotropic plasticity :...
.
Factors influencing yield stress
The stress at which yield occurs is dependent on both the rate of deformation (strain rate) and, more significantly, the temperature at which the deformation occurs. Early work by Alder and Philips in 1954 found that the relationship between yield stress and strain rate (at constant temperature) was best described by a power law relationship of the form
where C is a constant and m is the strain rate sensitivity. The latter generally increases with temperature, and materials where m reaches a value greater than ~0.5 tend to exhibit super plastic behaviour.
Later, more complex equations were proposed that simultaneously dealt with both temperature and strain rate:
where α and A are constants and Z is the temperature-compensated strain-rate - often described by the Zener-Hollomon parameter:
where QHW is the activation energy for hot deformation and T is the absolute temperature.
Strengthening mechanisms
There are several ways in which crystalline and amorphous materials can be engineered to increase their yield strength. By altering dislocation density, impurity levels, grain size (in crystalline materials), the yield strength of the material can be fine tuned. This occurs typically by introducing defects such as impurities dislocations in the material. To move this defect (plastically deforming or yielding the material), a larger stress must be applied. This thus causes a higher yield stress in the material. While many material properties depend only on the composition of the bulk material, yield strength is extremely sensitive to the materials processing as well for this reason.These mechanisms for crystalline materials include
- Work HardeningWork hardeningWork hardening, also known as strain hardening or cold working, is the strengthening of a metal by plastic deformation. This strengthening occurs because of dislocation movements within the crystal structure of the material. Any material with a reasonably high melting point such as metals and...
- Solid Solution StrengtheningSolid solution strengtheningSolid solution strengthening is a type of alloying that can be used to improve the strength of a pure metal. The technique works by adding atoms of one element to the crystalline lattice of another element . The alloying element diffuses into the matrix, forming a solid solution...
- Particle/Precipitate StrengtheningPrecipitation strengtheningPrecipitation hardening, also called age hardening, is a heat treatment technique used to increase the yield strength of malleable materials, including most structural alloys of aluminium, magnesium, nickel and titanium, and some stainless steels...
- Grain boundary strengtheningGrain boundary strengtheningGrain-boundary strengthening is a method of strengthening materials by changing their average crystallite size...
Work HardeningWork hardeningWork hardening, also known as strain hardening or cold working, is the strengthening of a metal by plastic deformation. This strengthening occurs because of dislocation movements within the crystal structure of the material. Any material with a reasonably high melting point such as metals and...
Where deforming the material will introduce dislocationDislocation
In materials science, a dislocation is a crystallographic defect, or irregularity, within a crystal structure. The presence of dislocations strongly influences many of the properties of materials...
s, which increases their density in the material. This increases the yield strength of the material, since now more stress must be applied to move these dislocations through a crystal lattice. Dislocations can also interact with each other, becoming entangled.
The governing formula for this mechanism is:
where
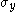is the yield stress, G is the shear elastic modulus, b is the magnitude of the Burgers vectorBurgers vector
The Burgers vector, named after Dutch physicist Jan Burgers, is a vector, often denoted b, that represents the magnitude and direction of the lattice distortion of dislocation in a crystal lattice....
, and
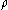is the dislocation density.Solid Solution StrengtheningSolid solution strengtheningSolid solution strengthening is a type of alloying that can be used to improve the strength of a pure metal. The technique works by adding atoms of one element to the crystalline lattice of another element . The alloying element diffuses into the matrix, forming a solid solution...
By alloyAlloy
An alloy is a mixture or metallic solid solution composed of two or more elements. Complete solid solution alloys give single solid phase microstructure, while partial solutions give two or more phases that may or may not be homogeneous in distribution, depending on thermal history...
ing the material, impurity atoms in low concentrations will occupy a lattice position directly below a dislocation, such as directly below an extra half plane defect. This relieves a tensile strain directly below the dislocation by filling that empty lattice space with the impurity atom.
The relationship of this mechanism goes as:
where
is the shear stressShear stress
A shear stress, denoted \tau\, , is defined as the component of stress coplanar with a material cross section. Shear stress arises from the force vector component parallel to the cross section...
, related to the yield stress, G and b are the same as in the above example, C_s is the concentration of solute and
is the strain induced in the lattice due to adding the impurity.Particle/Precipitate StrengtheningPrecipitation strengtheningPrecipitation hardening, also called age hardening, is a heat treatment technique used to increase the yield strength of malleable materials, including most structural alloys of aluminium, magnesium, nickel and titanium, and some stainless steels...
Where the presence of a secondary phase will increase yield strength by blocking the motion of dislocations within the crystal. A line defect that, while moving through the matrix, will be forced against a small particle or precipitate of the material. Dislocations can move through this particle either by shearing the particle, or by a process known as bowing or ringing, in which a new ring of dislocations is created around the particle.The shearing formula goes as:
and the bowing/ringing formula:
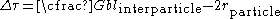
In these formulas,
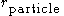is the particle radius, 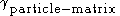is the surface tension between the matrix and the particle, 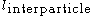is the distance between the particles.Grain boundary strengtheningGrain boundary strengtheningGrain-boundary strengthening is a method of strengthening materials by changing their average crystallite size...
Where a buildup of dislocations at a grain boundary causes a repulsive force between dislocations. As grain size decreases, the surface area to volume ratio of the grain increases, allowing more buildup of dislocations at the grain edge. Since it requires a lot of energy to move dislocations to another grain, these dislocations build up along the boundary, and increase the yield stress of the material. Also known as Hall-Petch strengthening, this type of strengthening is governed by the formula: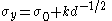where
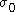is the stress required to move dislocations,
- k is a material constant, and
- d is the grain size.
Testing
Yield strength testing involves taking a small sample with a fixed cross-section area, and then pulling it with a controlled, gradually increasing force until the sample changes shape or breaks. Longitudinal and/or transverse strain is recorded using mechanical or optical extensometers.Indentation hardness
Indentation hardness
Indentation hardness tests are used to determine the hardness of a material to deformation. Several such tests exist, wherein the examined material is indented until an impression is formed; these tests can be performed on a macroscopic or microscopic scale....
correlates linearly with tensile strength for most steels. Hardness testing can therefore be an economical substitute for tensile testing, as well as providing local variations in yield strength due to e.g. welding or forming operations.
Implications for structural engineering
Yielded structures have a lower stiffness, leading to increased deflections and decreased buckling strength. The structure will be permanently deformed when the load is removed, and may have residual stresses. Engineering metals display strain hardening, which implies that the yield stress is increased after unloading from a yield state. Highly optimized structures, such as airplane beams and components, rely on yielding as a fail-safe failure mode. No safety factor is therefore needed when comparing limit loads (the highest loads expected during normal operation) to yield criteria.Typical yield and ultimate strengths
Note: many of the values depend on manufacturing process and purity/composition.| Material | Yield strength (MPa) | Ultimate strength (MPa) | Density (g/cm³) | free breaking length (km) |
|---|---|---|---|---|
| ASTM A36 steel A36 steel A36 steel is a standard steel alloy which is a common structural steel used in the United States.The A36 standard was established by the standards organization ASTM International.- Properties :... |
250 | 400 | 7.8 | 3.2 |
| Steel, API 5L X65 | 448 | 531 | 7.8 | 5.8 |
| Steel, high strength alloy ASTM A514 | 690 | 760 | 7.8 | 9.0 |
| Steel, prestressing strands | 1650 | 1860 | 7.8 | 21.6 |
| Piano wire Piano wire Piano wire, or "music wire", is a specialized type of wire made for use in piano strings, as well as many other purposes. It is made from tempered high-carbon steel, also known as spring steel.-Manufacture and use:... |
2200–2482 | 7.8 | 28.7 | |
| Carbon Fiber Carbon fiber Carbon fiber, alternatively graphite fiber, carbon graphite or CF, is a material consisting of fibers about 5–10 μm in diameter and composed mostly of carbon atoms. The carbon atoms are bonded together in crystals that are more or less aligned parallel to the long axis of the fiber... (CF, CFK) |
5650 | 1.75 | ||
| High density polyethylene High density polyethylene High-density polyethylene or polyethylene high-density is a polyethylene thermoplastic made from petroleum. It takes 1.75 kilograms of petroleum to make one kilogram of HDPE... (HDPE) |
26-33 | 37 | 0.95 | 2.8 |
| Polypropylene Polypropylene Polypropylene , also known as polypropene, is a thermoplastic polymer used in a wide variety of applications including packaging, textiles , stationery, plastic parts and reusable containers of various types, laboratory equipment, loudspeakers, automotive components, and polymer banknotes... |
12-43 | 19.7-80 | 0.91 | 1.3 |
| Stainless steel Stainless steel In metallurgy, stainless steel, also known as inox steel or inox from French "inoxydable", is defined as a steel alloy with a minimum of 10.5 or 11% chromium content by mass.... AISI 302 - Cold-rolled |
520 | 860 | ||
| Cast iron Cast iron Cast iron is derived from pig iron, and while it usually refers to gray iron, it also identifies a large group of ferrous alloys which solidify with a eutectic. The color of a fractured surface can be used to identify an alloy. White cast iron is named after its white surface when fractured, due... 4.5% C, ASTM A-48 |
* | 172 | 7.20 | 2.4 |
| Titanium alloy Titanium alloy Titanium alloys are metallic materials which contain a mixture of titanium and other chemical elements. Such alloys have very high tensile strength and toughness , light weight, extraordinary corrosion resistance, and ability to withstand extreme temperatures... (6% Al, 4% V) |
830 | 900 | 4.51 | 18.8 |
| Aluminium alloy Aluminium alloy Aluminium alloys are alloys in which aluminium is the predominant metal. The typical alloying elements are copper, magnesium, manganese, silicon and zinc. There are two principal classifications, namely casting alloys and wrought alloys, both of which are further subdivided into the categories... 2014-T6 |
400 | 455 | 2.7 | 15.1 |
| Copper Copper Copper is a chemical element with the symbol Cu and atomic number 29. It is a ductile metal with very high thermal and electrical conductivity. Pure copper is soft and malleable; an exposed surface has a reddish-orange tarnish... 99.9% Cu |
70 | 220 | 8.92 | 0.8 |
| Cupronickel Cupronickel Cupronickel or copper-nickel or "cupernickel" is an alloy of copper that contains nickel and strengthening elements, such as iron and manganese. Cupronickel is highly resistant to corrosion in seawater, because its electrode potential is adjusted to be neutral with regard to seawater... 10% Ni, 1.6% Fe, 1% Mn, balance Cu |
130 | 350 | 8.94 | 1.4 |
| Brass Brass Brass is an alloy of copper and zinc; the proportions of zinc and copper can be varied to create a range of brasses with varying properties.In comparison, bronze is principally an alloy of copper and tin... |
approx. 200+ | 550 | 5.3 | 3.8 |
| Spider silk Spider silk Spider silk is a protein fiber spun by spiders. Spiders use their silk to make webs or other structures, which function as nets to catch other animals, or as nests or cocoons for protection for their offspring... |
1150 (??) | 1400 | 1.31 | 109 |
| Silkworm silk | 500 | 25 | ||
| Aramid Aramid Aramid fibers are a class of heat-resistant and strong synthetic fibers. They are used in aerospace and military applications, for ballistic rated body armor fabric and ballistic composites, in bicycle tires, and as an asbestos substitute. The name is a portmanteau of "aromatic polyamide"... (Kevlar Kevlar Kevlar is the registered trademark for a para-aramid synthetic fiber, related to other aramids such as Nomex and Technora. Developed at DuPont in 1965, this high strength material was first commercially used in the early 1970s as a replacement for steel in racing tires... or Twaron Twaron Twaron is the brandname of Teijin Aramid for a para-aramid. It is a heat-resistant and strong synthetic fibre developed in the early 1970s by the Dutch company AKZO, division Enka, later Akzo Industrial Fibers. The research name of the para-aramid fibre was originally Fiber X, but it was soon... ) |
3620 | 1.44 | 256.3 | |
| UHMWPE Ultra high molecular weight polyethylene Ultra-high-molecular-weight polyethylene , also known as high-modulus polyethylene or high-performance polyethylene , is a subset of the thermoplastic polyethylene. It has extremely long chains, with molecular weight numbering in the millions, usually between 2 and 6 million... |
2400 | 0.97 | 400 | |
| Bone Bone Bones are rigid organs that constitute part of the endoskeleton of vertebrates. They support, and protect the various organs of the body, produce red and white blood cells and store minerals. Bone tissue is a type of dense connective tissue... (limb) |
104-121 | 130 | 3 | |
| Nylon Nylon Nylon is a generic designation for a family of synthetic polymers known generically as polyamides, first produced on February 28, 1935, by Wallace Carothers at DuPont's research facility at the DuPont Experimental Station... , type 6/6 |
45 | 75 | 2 | |
| *Grey cast iron does not have a well defined yield strength because the stress-strain relationship is atypical. The yield strength can vary from 65 to 80% of the tensile strength. | ||||
| Young's modulus (GPa) | Proof or yield stress (MPa) | Ultimate Tensile Strength (MPa) |
|
|---|---|---|---|
| Aluminium Aluminium Aluminium or aluminum is a silvery white member of the boron group of chemical elements. It has the symbol Al, and its atomic number is 13. It is not soluble in water under normal circumstances.... |
70 | 15-20 | 40-50 |
| Copper Copper Copper is a chemical element with the symbol Cu and atomic number 29. It is a ductile metal with very high thermal and electrical conductivity. Pure copper is soft and malleable; an exposed surface has a reddish-orange tarnish... |
130 | 33 | 210 |
| Iron Iron Iron is a chemical element with the symbol Fe and atomic number 26. It is a metal in the first transition series. It is the most common element forming the planet Earth as a whole, forming much of Earth's outer and inner core. It is the fourth most common element in the Earth's crust... |
211 | 80-100 | 350 |
| Nickel Nickel Nickel is a chemical element with the chemical symbol Ni and atomic number 28. It is a silvery-white lustrous metal with a slight golden tinge. Nickel belongs to the transition metals and is hard and ductile... |
170 | 14-35 | 140-195 |
| Silicon Silicon Silicon is a chemical element with the symbol Si and atomic number 14. A tetravalent metalloid, it is less reactive than its chemical analog carbon, the nonmetal directly above it in the periodic table, but more reactive than germanium, the metalloid directly below it in the table... |
107 | 5000-9000 | |
| Tantalum Tantalum Tantalum is a chemical element with the symbol Ta and atomic number 73. Previously known as tantalium, the name comes from Tantalus, a character in Greek mythology. Tantalum is a rare, hard, blue-gray, lustrous transition metal that is highly corrosion resistant. It is part of the refractory... |
186 | 180 | 200 |
| Tin Tin Tin is a chemical element with the symbol Sn and atomic number 50. It is a main group metal in group 14 of the periodic table. Tin shows chemical similarity to both neighboring group 14 elements, germanium and lead and has two possible oxidation states, +2 and the slightly more stable +4... |
47 | 9-14 | 15-200 |
| Titanium Titanium Titanium is a chemical element with the symbol Ti and atomic number 22. It has a low density and is a strong, lustrous, corrosion-resistant transition metal with a silver color.... |
120 | 100-225 | 240-370 |
| Tungsten Tungsten Tungsten , also known as wolfram , is a chemical element with the chemical symbol W and atomic number 74.A hard, rare metal under standard conditions when uncombined, tungsten is found naturally on Earth only in chemical compounds. It was identified as a new element in 1781, and first isolated as... |
411 | 550 | 550-620 |
See also
- Piola-Kirchhoff stress tensor
- Strain tensor
- Stress concentrationStress concentrationA stress concentration is a location in an object where stress is concentrated. An object is strongest when force is evenly distributed over its area, so a reduction in area, e.g. caused by a crack, results in a localized increase in stress...
- Linear elasticityLinear elasticityLinear elasticity is the mathematical study of how solid objects deform and become internally stressed due to prescribed loading conditions. Linear elasticity models materials as continua. Linear elasticity is a simplification of the more general nonlinear theory of elasticity and is a branch of...
- Yield curve (physics)Yield curve (physics)In material science, the yield curve describes the behaviour of a plastic material.In a two-dimensional stress system the pliability or stiffness of the material can be plotted on a graph in the form of a yield curve. The curve expresses the failure stress, the combination of stresses at which the...
- Tensile strengthTensile strengthUltimate tensile strength , often shortened to tensile strength or ultimate strength, is the maximum stress that a material can withstand while being stretched or pulled before necking, which is when the specimen's cross-section starts to significantly contract...
- Elastic modulusElastic modulusAn elastic modulus, or modulus of elasticity, is the mathematical description of an object or substance's tendency to be deformed elastically when a force is applied to it...
- Virial stress
- Yield surfaceYield surfaceA yield surface is a five-dimensional surface in the six-dimensional space of stresses. The yield surface is usually convex and the state of stress of inside the yield surface is elastic. When the stress state lies on the surface the material is said to have reached its yield point and the...