For the leaf bug, see Miridae

Miridae

The large and diverse insect family Miridae contains the plant bugs, leaf bugs, and grass bugs, and may also be known as capsid bugs. It is the largest family of true bugs belonging to the suborder Heteroptera, with over 10,000 known species and new ones constantly being described...

.

A capsid is the protein shell of a virus. It consists of several oligomer

Oligomer

In chemistry, an oligomer is a molecule that consists of a few monomer units , in contrast to a polymer that, at least in principle, consists of an unlimited number of monomers. Dimers, trimers, and tetramers are oligomers. Many oils are oligomeric, such as liquid paraffin...

ic structural subunits made of protein

Protein

Proteins are biochemical compounds consisting of one or more polypeptides typically folded into a globular or fibrous form, facilitating a biological function. A polypeptide is a single linear polymer chain of amino acids bonded together by peptide bonds between the carboxyl and amino groups of...

 called protomer

Protomer

In structural biology, a protomer is the structural unit of an oligomeric protein. A protomer can be a protein subunit or several different subunits, that assemble in a defined stoichiometry to form an oligomer. The protomer is the smallest subset of different subunits that form the oligomer. The...

s. The observable 3-dimensional morphological subunits, which may or may not correspond to individual proteins, are called capsomere

Capsomere

The capsomere is a basic subunit of the capsid, an outer covering of protein that protects the genetic material of a virus. Capsomeres self-assemble to form the capsid....

s. The capsid encloses the genetic material of the virus.

Capsids are broadly classified according to their structure. The majority of viruses have capsids with either helical or icosahedral  structure. Some viruses, such as bacteriophages, have developed more complicated structures due to constraints of elasticity and electrostatics. The icosahedral shape, which has 20 equilateral triangular faces, approximates a sphere

Sphere

A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...

, while the helical shape is cylindrical. The capsid faces may consist of one or more proteins. For example, the foot-and-mouth disease

Foot-and-mouth disease

Foot-and-mouth disease or hoof-and-mouth disease is an infectious and sometimes fatal viral disease that affects cloven-hoofed animals, including domestic and wild bovids...

 virus capsid has faces consisting of three proteins named VP1–3.

Some viruses are enveloped, meaning that the capsid is coated with a lipid membrane known as the viral envelope

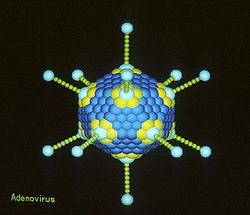
Viral envelope

Many viruses have viral envelopes covering their protein capsids. The envelopes typically are derived from portions of the host cell membranes , but include some viral glycoproteins. Functionally, viral envelopes are used to help viruses enter host cells...

. The envelope is acquired by the capsid from an intracellular membrane in the virus' host; some examples would include the inner nuclear membrane, the golgi

Golgi

Golgi may refer to:*Camillo Golgi , Italian physician and scientist after which the following terms are named:**Golgi apparatus , an organelle in the eukaryotic cell...

 membrane, and the cell's outer membrane

Cell membrane

The cell membrane or plasma membrane is a biological membrane that separates the interior of all cells from the outside environment. The cell membrane is selectively permeable to ions and organic molecules and controls the movement of substances in and out of cells. It basically protects the cell...

.

Once the virus has infected the cell, it will start replicating itself, using the mechanisms of the infected host cell. During this process, new capsid subunits are synthesized according to the genetic material of the virus, using the protein biosynthesis

Protein biosynthesis

Protein biosynthesis is the process in which cells build or manufacture proteins. The term is sometimes used to refer only to protein translation but more often it refers to a multi-step process, beginning with amino acid synthesis and transcription of nuclear DNA into messenger RNA, which is then...

 mechanism of the cell. During the assembly process, a portal subunit is assembled at one vertex of the capsid. Through this portal, viral DNA

DNA

Deoxyribonucleic acid is a nucleic acid that contains the genetic instructions used in the development and functioning of all known living organisms . The DNA segments that carry this genetic information are called genes, but other DNA sequences have structural purposes, or are involved in...

 or RNA

RNA

Ribonucleic acid , or RNA, is one of the three major macromolecules that are essential for all known forms of life....

 is transported into the capsid. The structure and assembly of the herpes virus capsid portal protein has been imaged via cryo-electron microscopy

Cryo-electron microscopy

Cryo-electron microscopy , or electron cryomicroscopy, is a form of transmission electron microscopy where the sample is studied at cryogenic temperatures...

.

It is this capsid or protein shell that makes protective vaccines a possibility. Structural analyses of major capsid protein (MCP) architectures have been used to categorise viruses into families. For example, the bacteriophage PRD1, Paramecium bursaria Chlorella algal virus, and mammalian adenovirus

Adenoviridae

Adenoviruses are medium-sized , nonenveloped icosahedral viruses composed of a nucleocapsid and a double-stranded linear DNA genome...

 have been placed in the same family.

T-number

Icosahedral virus capsids are typically assigned a T-number to describe the relation between the number of pentagons and hexagons i.e. their quasi-symmetry in the capsid shell. The T-number idea was originally developed to explain the quasi-symmetry by Caspar and Klug in 1962.

For example, a purely icosahedral virus has a T-number of 1 (usually written, T=1) and a truncated icosahedron

Truncated icosahedron

In geometry, the truncated icosahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids whose faces are two or more types of regular polygons.It has 12 regular pentagonal faces, 20 regular hexagonal faces, 60 vertices and 90 edges....

 is assigned T=3. The T-number is calculated by (1) applying a grid to the surface of the virus with coordinates h and k, (2) counting the number of steps between successive pentagons on the virus surface, (3) applying the formula:
=

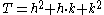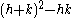
where and h and k are the distances between the successive pentagons on the virus surface for each axis (see figure on right). The larger the T-number the more hexagons are present relative to the pentagons.

Representation of Viral Capsid T-numbers up to (6,6)

capsid parameters		hexagon/pentagon system Simple polytope In geometry, a d-dimensional simple polytope is a d-dimensional polytope each of whose vertices are adjacent to exactly d edges . The vertex figure of a simple d-polytope is a -simplex....				triangle system Simplicial polytope In geometry, a simplicial polytope is a d-polytope whose facets are all simplices.For example, a simplicial polyhedron contains only triangular faces and corresponds via Steinitz's theorem to a maximal planar graph....
(h,k)	T	# hex	Conway notation Conway polyhedron notation Conway polyhedron notation is used to describe polyhedra based on a seed polyhedron modified by various operations.The seed polyhedra are the Platonic solids, represented by their first letter of their name ; the prisms , antiprisms and pyramids...	image	geometric name	# tri	Conway notation Conway polyhedron notation Conway polyhedron notation is used to describe polyhedra based on a seed polyhedron modified by various operations.The seed polyhedra are the Platonic solids, represented by their first letter of their name ; the prisms , antiprisms and pyramids...	image	geometric name
(1,0)	1	0	D		Dodecahedron	20	I		Icosahedron Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
(1,1)	3	20	tI dkD		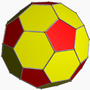Truncated icosahedron Truncated icosahedron In geometry, the truncated icosahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids whose faces are two or more types of regular polygons.It has 12 regular pentagonal faces, 20 regular hexagonal faces, 60 vertices and 90 edges....	60	kD		Pentakis dodecahedron Pentakis dodecahedron In geometry, a pentakis dodecahedron is a Catalan solid. Its dual is the truncated icosahedron, an Archimedean solid.It can be seen as a dodecahedron with a pentagonal pyramid covering each face; that is, it is the Kleetope of the dodecahedron...
(2,0)	4	30	cD=t5daD		Truncated rhombic triacontahedron Truncated rhombic triacontahedron The truncated rhombic triacontahedron is a convex polyhedron constructed as a truncation of the rhombic triacontahedron. It can more accurately be called a pentatruncated rhombic triacontahedron because only the order-5 vertices are truncated....	80	k5aD		Pentakis icosidodecahedron Pentakis icosidodecahedron The pentakis icosidodecahedron is a convex polyhedron with 80 triangular faces, 120 edges, and 42 vertices. It a dual of the truncated rhombic triacontahedron....
(2,1)	7	60	dk5sD			140	k5sD		Pentakis snub dodecahedron Pentakis snub dodecahedron The pentakis snub dodecahedron is a convex polyhedron with 140 triangular faces, 210 edges, and 72 vertices. Like the snub dodecahedron it has chiral Icosahedral symmetry....
(3,0)	9	80	dktI			180	ktI		Hexapentakis truncated icosahedron
(2,2)	12	110	dkt5daD			240	kt5daD		Hexapentakis truncated rhombic triacontahedron
(3,1)	13	120				260
(4,0)	16	150	ccD			320	dccD
(3,2)	19	180				380
(4,1)	21	200	dk5k6stI tk5sD			420	k5k6stI kdk5sD		Hexapentakis snub truncated icosahedron
(5,0)	25	240				500
(3,3)	27	260	tktI			540	kdktI
(4,2)	28
(5,1)	31
(6,0)	36	350	tkt5daD			720	kdkt5daD
(4,3)	37
(5,2)	39
(6,1)	43
(4,4)	48	470	dadkt5daD			960	k5k6akdk5aD
(6,2)	48
(5,3)	49
(5,4)	61
(6,3)	64
(5,5)	75
(6,4)	76
(6,5)	91
(6,6)	108
...

T-numbers can be represented in different ways, for example T=1 can only be represented as a Icosahedron

Icosahedron

In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....

 or a Dodecahedron and, depending on the type of quasi-symmetry, T=3 can be presented as a Truncated dodecahedron

Truncated dodecahedron

In geometry, the truncated dodecahedron is an Archimedean solid. It has 12 regular decagonal faces, 20 regular triangular faces, 60 vertices and 90 edges.- Geometric relations :...

, an Icosidodecahedron

Icosidodecahedron

In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon...

, or a Truncated icosahedron

Truncated icosahedron

In geometry, the truncated icosahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids whose faces are two or more types of regular polygons.It has 12 regular pentagonal faces, 20 regular hexagonal faces, 60 vertices and 90 edges....

 and their respective duals a Triakis icosahedron

Triakis icosahedron

In geometry, the triakis icosahedron is an Archimedean dual solid, or a Catalan solid. Its dual is the truncated dodecahedron.It can be seen as an icosahedron with triangular pyramids augmented to each face; that is, it is the Kleetope of the icosahedron...

, a Rhombic triacontahedron

Rhombic triacontahedron

In geometry, the rhombic triacontahedron is a convex polyhedron with 30 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. It is the polyhedral dual of the icosidodecahedron, and it is a zonohedron....

, or a Pentakis dodecahedron

Pentakis dodecahedron

In geometry, a pentakis dodecahedron is a Catalan solid. Its dual is the truncated icosahedron, an Archimedean solid.It can be seen as a dodecahedron with a pentagonal pyramid covering each face; that is, it is the Kleetope of the dodecahedron...

.