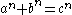Wiles' proof of Fermat's Last Theorem
Encyclopedia

Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
of the modularity theorem for semistable elliptic curve
Semistable elliptic curve
In algebraic geometry, a semistable abelian variety is an abelian variety defined over a global or local field, which is characterized by how it reduces at the primes of the field....
s released by Andrew Wiles
Andrew Wiles
Sir Andrew John Wiles KBE FRS is a British mathematician and a Royal Society Research Professor at Oxford University, specializing in number theory...
, which, together with Ribet's theorem, provides a proof for Fermat's Last Theorem
Fermat's Last Theorem
In number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
. Wiles first announced his proof in June 1993 in a version that was soon recognized as having a serious gap. The widely accepted version of the proof was released by Andrew Wiles in September 1994, and published in 1995. The proof uses many techniques from algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
and number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, and has many ramifications in these branches of mathematics. It also uses standard constructions of modern algebraic geometry, such as the category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of schemes
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
and Iwasawa theory
Iwasawa theory
In number theory, Iwasawa theory is the study of objects of arithmetic interest over infinite towers of number fields. It began as a Galois module theory of ideal class groups, initiated by Kenkichi Iwasawa, in the 1950s, as part of the theory of cyclotomic fields. In the early 1970s, Barry Mazur...
, and other 20th century techniques not available to Fermat.
The proof itself is over 100 pages long and consumed seven years of Wiles's research time. Among other honors for his accomplishment, he was knighted.
Progress of the previous decades
Fermat's Last Theorem states that no nontrivial integer solutions exist for the equationif n is an integer greater than two.
In the 1950s and 1960s a connection between elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
s and modular form
Modular form
In mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...
s was conjectured by the Japanese mathematician Goro Shimura
Goro Shimura
is a Japanese mathematician, and currently a professor emeritus of mathematics at Princeton University.Shimura was a colleague and a friend of Yutaka Taniyama...
based on some ideas that Yutaka Taniyama
Yutaka Taniyama
Yutaka Taniyama was a Japanese mathematician known for the Taniyama-Shimura conjecture.-Contribution:...
posed. In the West it became well known through a 1967 paper by André Weil
André Weil
André Weil was an influential mathematician of the 20th century, renowned for the breadth and quality of his research output, its influence on future work, and the elegance of his exposition. He is especially known for his foundational work in number theory and algebraic geometry...
. With Weil giving conceptual evidence for it, it is sometimes called the Shimura-Taniyama-Weil conjecture
Shimura–Taniyama theorem
In mathematics the modularity theorem states that elliptic curves over the field of rational numbers are related to modular forms...
. It states that every rational
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
elliptic curve is modular
Classical modular curve
In number theory, the classical modular curve is an irreducible plane algebraic curve given by an equationwhere for the j-invariant j,is a point on the curve. The curve is sometimes called X0, though often that is used for the abstract algebraic curve for which there exist various models...
.
On a separate branch of development, in the late 1960s, Yves Hellegouarch came up with the idea of associating solutions (a,b,c) of Fermat's equation with a completely different mathematical object: an elliptic curve. The curve consists of all points in the plane whose coordinates (x, y) satisfy the relation
Such an elliptic curve would enjoy very special properties, which are due to the appearance of high powers of integers in its equation and the fact that an + bn = cn is a nth power as well.
In 1982–1985, Gerhard Frey
Gerhard Frey
Gerhard Frey is a German mathematician, known for his work in number theory. His Frey curve, a construction of an elliptic curve from a purported solution to the Fermat equation, was central to Wiles' proof of Fermat's Last Theorem....
called attention to the unusual properties of the same curve as Hellegouarch, now called a Frey curve. This provided a bridge between Fermat and Taniyama by showing that a counterexample to Fermat's Last Theorem would create such a curve that would not be modular
Modular curve
In number theory and algebraic geometry, a modular curve Y is a Riemann surface, or the corresponding algebraic curve, constructed as a quotient of the complex upper half-plane H by the action of a congruence subgroup Γ of the modular group of integral 2×2 matrices SL...
. Again, the conjecture says that each elliptic curve with rational
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
coefficients can be constructed in an entirely different way, not by giving its equation but by using modular functions to parametrize coordinates x and y of the points on it. Thus, according to the conjecture, any elliptic curve over Q would have to be a modular elliptic curve
Modular elliptic curve
A modular elliptic curve is an elliptic curve E that admits a parametrisation X0 → E by a modular curve. This is not the same as a modular curve that happens to be an elliptic curve, and which could be called an elliptic modular curve...
, yet if a solution to Fermat's equation with non-zero a, b, c and p greater than 2 existed, the corresponding curve would not be modular, resulting in a contradiction.
In 1985, Jean-Pierre Serre
Jean-Pierre Serre
Jean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...
proposed that a Frey curve could not be modular and provided a partial proof of this. This showed that a proof of the semistable
Semistable elliptic curve
In algebraic geometry, a semistable abelian variety is an abelian variety defined over a global or local field, which is characterized by how it reduces at the primes of the field....
case of the Taniyama-Shimura conjecture would imply Fermat's Last Theorem. Serre did not provide a complete proof and what was missing became known as the epsilon conjecture
Epsilon theorem
In mathematics, Ribet's theorem is a statement in number theory concerning properties of Galois representations associated with modular forms. It was proposed by Jean-Pierre Serre and proved by Ken Ribet. The proof of epsilon conjecture was a significant step towards the proof of Fermat's Last...
or ε-conjecture. Serre's main interest was in an even more ambitious conjecture, Serre's conjecture
Serre conjecture (number theory)
In mathematics, Jean-Pierre Serre conjectured the following result regarding two-dimensional Galois representations. This was a significant step in number theory, though this was not realised for at least a decade.-Formulation:...
on modular Galois representations, which would imply the Taniyama–Shimura conjecture. Although in the preceding twenty or thirty years a lot of evidence had been accumulated to form conjectures about elliptic curves, the main reason to believe that these various conjectures were true lay not in the numerical confirmations, but in a remarkably coherent and attractive mathematical picture that they presented. Moreover, it could have happened that one or more of these conjectures were actually false.
In the summer of 1986, Ken Ribet
Kenneth Alan Ribet
Kenneth Alan "Ken" Ribet is an American mathematician, currently a professor of mathematics at the University of California, Berkeley. His mathematical interests include algebraic number theory and algebraic geometry....
succeeded in proving the epsilon conjecture. (His article was published in 1990.) He demonstrated that, just as Frey had anticipated, a special case of the Taniyama–Shimura conjecture (still unproven at the time), together with the now proven epsilon conjecture, implies Fermat's Last Theorem. Thus, if the Taniyama–Shimura conjecture holds for a class of elliptic curves called semistable elliptic curves, then Fermat's Last Theorem would be true.
General approach of proof
Given an elliptic curve E over the field Q of rational numbers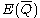 , for every prime power
, for every prime power 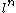 , there exists a homomorphism
, there exists a homomorphismHomomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
from the absolute Galois group
Absolute Galois group
In mathematics, the absolute Galois group GK of a field K is the Galois group of Ksep over K, where Ksep is a separable closure of K. Alternatively it is the group of all automorphisms of the algebraic closure of K that fix K. The absolute Galois group is unique up to isomorphism...
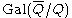
to
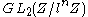 ,
,the group of invertible 2 by 2 matrices whose entries are integers (
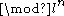 ). This is because
). This is because 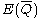 , the points of E over
, the points of E over 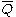 , form an abelian group
, form an abelian groupAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
, on which
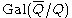 acts; the subgroup of elements x such that
acts; the subgroup of elements x such that 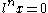 is just
is just 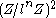 , and an automorphism
, and an automorphismAutomorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
of this group is a matrix of the type described.
Less obvious is that given a modular form of a certain special type, a Hecke eigenform with eigenvalues in Q, one also gets a homomorphism from the absolute Galois group
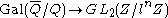 .:
.:This goes back to Eichler and Shimura. The idea is that the Galois group acts first on the modular curve on which the modular form is defined, thence on the Jacobian variety
Jacobian variety
In mathematics, the Jacobian variety J of a non-singular algebraic curve C of genus g is the moduli space of degree 0 line bundles...
of the curve, and finally on the points of
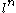 power order on that Jacobian. The resulting representation is not usually 2-dimensional, but the Hecke operator
power order on that Jacobian. The resulting representation is not usually 2-dimensional, but the Hecke operatorHecke operator
In mathematics, in particular in the theory of modular forms, a Hecke operator, studied by , is a certain kind of "averaging" operator that plays a significant role in the structure of vector spaces of modular forms and more general automorphic representations....
s cut out a 2-dimensional piece. It is easy to demonstrate that these representations come from some elliptic curve but the converse is the difficult part to prove.
Instead of trying to go directly from the elliptic curve to the modular form, one can first pass to the (
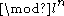 ) representation for some l and n, and from that to the modular form. In the case l=3 and n=1, results of the Langlands-Tunnell theorem show that the (mod 3) representation of any elliptic curve over Q comes from a modular form. The basic strategy is to use induction on n to show that this is true for l=3 and any n, that ultimately there is a single modular form that works for all n. To do this, one uses a counting argument, comparing the number of ways in which one can lift
) representation for some l and n, and from that to the modular form. In the case l=3 and n=1, results of the Langlands-Tunnell theorem show that the (mod 3) representation of any elliptic curve over Q comes from a modular form. The basic strategy is to use induction on n to show that this is true for l=3 and any n, that ultimately there is a single modular form that works for all n. To do this, one uses a counting argument, comparing the number of ways in which one can liftLift (mathematics)
In the branch of mathematics called category theory, given a morphism f from an object X to an object Y, and a morphism g from an object Z to Y, a lift of f to Z is a morphism h from X to Z such that gh = f.A basic example in topology is lifting a path in one space to a path in a covering space...
a (
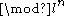 ) Galois representation to (
) Galois representation to (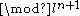 ) and the number of ways in which one can lift a (
) and the number of ways in which one can lift a (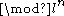 ) modular form. An essential point is to impose a sufficient set of conditions on the Galois representation; otherwise, there will be too many lifts and most will not be modular. These conditions should be satisfied for the representations coming from modular forms and those coming from elliptic curves. If the original (mod 3) representation has an image which is too small, one runs into trouble with the lifting argument, and in this case, there is a final trick, which has since taken on a life of its own with the subsequent work on the Serre Modularity Conjecture
) modular form. An essential point is to impose a sufficient set of conditions on the Galois representation; otherwise, there will be too many lifts and most will not be modular. These conditions should be satisfied for the representations coming from modular forms and those coming from elliptic curves. If the original (mod 3) representation has an image which is too small, one runs into trouble with the lifting argument, and in this case, there is a final trick, which has since taken on a life of its own with the subsequent work on the Serre Modularity ConjectureSerre conjecture (number theory)
In mathematics, Jean-Pierre Serre conjectured the following result regarding two-dimensional Galois representations. This was a significant step in number theory, though this was not realised for at least a decade.-Formulation:...
. The idea involves the interplay between the (mod 3) and (mod 5) representations. See Chapter 5 of the Wiles paper for this 3/5 switch.
Wiles's proof
Shortly after learning of the proof of the epsilon conjecture, it was clear that a proof that all rational semistable elliptic curves are modular would also constitute a proof of Fermat's Last TheoremFermat's Last Theorem
In number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
. Wiles decided to conduct his research exclusively towards finding a proof for the Taniyama-Shimura conjecture. Many mathematicians thought the Taniyama-Shimura conjecture was inaccessible to prove because the modular forms and elliptic curves seem to be unrelated.
Wiles opted to attempt to "count" and match elliptic curves to counted modular forms. He found that this direct approach was not working, so he transformed the problem by instead matching the Galois representations of the elliptic curves to modular forms. Wiles denotes this matching (or mapping) that, more specifically, is a ring homomorphism
Ring homomorphism
In ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
:
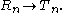
R is a deformation ring and T is a Hecke ring
Hecke algebra
In mathematics, the Iwahori–Hecke algebra, or Hecke algebra, named for Erich Hecke and Nagayoshi Iwahori, is a one-parameter deformation of the group algebra of a Coxeter group....
.
Wiles had the insight that in many cases this ring homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
could be a ring isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
. (Conjecture 2.16 in Chapter 2, §3) Wiles had the insight that the map between R and T is an isomorphism if and only if two abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s occurring in the theory are finite and have the same cardinality. This is sometimes referred to as the "numerical criterion". Given this result, one can see that Fermat's Last Theorem is reduced to a statement saying that two groups have the same order. Much of the text of the proof leads into topics and theorems related to ring theory
Ring theory
In abstract algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those familiar from the integers...
and commutation theory. The Goal is to verify that the map R → T is an isomorphism and ultimately that R=T. This is the long and difficult step. In treating deformations, Wiles defines four cases, with the flat deformation case requiring more effort to prove and is treated in a separate article in the same volume entitled "Ring-theoretic properties of certain Hecke algebra".
Gerd Faltings
Gerd Faltings
Gerd Faltings is a German mathematician known for his work in arithmetic algebraic geometry.From 1972 to 1978, he studied mathematics and physics at the University of Münster. In 1978 he received his PhD in mathematics and in 1981 he got the venia legendi in mathematics, both from the University...
, in his bulletin, on p. 745. gives this commutative diagram
Commutative diagram
In mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
:
--> T -> T/m
/ ^
R |
\ |
--> Z3 -> F3
or ultimately that R = T , indicating a complete intersection
Complete intersection
In mathematics, an algebraic variety V in projective space is a complete intersection if it can be defined by the vanishing of the number of homogeneous polynomials indicated by its codimension...
. Since Wiles cannot show that R=T directly, he does so through Z3, F3 and T/m via lifts
Lift (mathematics)
In the branch of mathematics called category theory, given a morphism f from an object X to an object Y, and a morphism g from an object Z to Y, a lift of f to Z is a morphism h from X to Z such that gh = f.A basic example in topology is lifting a path in one space to a path in a covering space...
.
In order to perform this matching, Wiles had to create a class number formula
Class number formula
In number theory, the class number formula relates many important invariants of a number field to a special value of its Dedekind zeta function-General statement of the class number formula:...
(CNF). He first attempted to use horizontal Iwasawa theory but that part of his work had an unresolved issue such that he could not create a CNF. At the end of the summer of 1991, he learned about a paper by Matthias Flach, using ideas of Victor Kolyvagin
Victor Kolyvagin
Victor Alexandrovich Kolyvagin is a Russian mathematician who wrote a series of papers on Euler systems, leading to breakthroughs on the Birch and Swinnerton-Dyer conjecture, and Iwasawa's conjecture for cyclotomic fields. His work also influenced Andrew Wiles's work on Fermat's Theorem.Kolyvagin...
to create a CNF, and so Wiles set his Iwasawa work aside. Wiles extended Flach's work in order to create a CNF. By the spring of 1993, his work covered all but a few families of elliptic curves. In early 1993, Wiles reviewed his argument beforehand with a Princeton colleague, Nick Katz
Nick Katz
Nicholas Michael Katz is an American mathematician, working in the fields of algebraic geometry, particularly on p-adic methods, monodromy and moduli problems, and number theory...
. His proof involved the Kolyvagin-Flach method, which he adopted after the Iwasawa method failed. In May 1993 while reading a paper by Mazur, Wiles had the insight that the 3/5 switch would resolve the final issues and would then cover all elliptic curves (again, see Chapter 5 of the paper for this 3/5 switch). Over the course of three lectures delivered at Isaac Newton Institute for Mathematical Sciences on June 21, 22, and 23 of 1993, Wiles announced his proof of the Taniyama–Shimura conjecture, and hence of Fermat's Last Theorem. There was a relatively large amount of press coverage afterwards.
After announcing his results, Katz was a referee on his manuscript and he asked Wiles a series of questions that led Wiles to recognize that the proof contained a gap. There was an error in a critical portion of the proof which gave a bound for the order of a particular group: the Euler system
Euler system
In mathematics, an Euler system is collection of compatible elements of Galois cohomology groups indexed by fields. They were introduced by in his work on Heegner points on modular elliptic curves, which was motivated by his earlier paper and the work of...
used to extend Flach's method was incomplete. Wiles and his former student Richard Taylor
Richard Taylor (mathematician)
-External links:**...
spent almost a year resolving it. Wiles indicates that on the morning of September 19, 1994 he realized that the specific reason why the Flach approach would not work directly suggested a new approach with the Iwasawa theory which resolved all of the previous issues with the latter and resulted in a CNF that was valid for all of the required cases. On 6 October Wiles sent the new proof to three colleagues including Faltings. The new proof was published and, despite its size, widely accepted as likely correct in its major components.
In his 1995 108 page article, Wiles divides the subject matter up into the following chapters (preceded here by page numbers):
- 443 Introduction
- Chapter 1
- 455 1. Deformations of Galois representations
- 472 2. Some computations of cohomologyCohomologyIn mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
groups - 475 3. Some results on subgroups of GL2(k)
- Chapter 2
- 479 1. The GorensteinGorenstein ringIn commutative algebra, a Gorenstein local ring is a Noetherian commutative local ring R with finite injective dimension, as an R-module. There are many equivalent conditions, some of them listed below, most dealing with some sort of duality condition....
property - 489 2. Congruences between Hecke rings
- 503 3. The main conjectures
- 479 1. The Gorenstein
- 517 Chapter 3 : Estimates for the Selmer group
- Chapter 4
- 525 1. The ordinary CMComplex multiplicationIn mathematics, complex multiplication is the theory of elliptic curves E that have an endomorphism ring larger than the integers; and also the theory in higher dimensions of abelian varieties A having enough endomorphisms in a certain precise sense In mathematics, complex multiplication is the...
case - 533 2. Calculation of η
- 525 1. The ordinary CM
- 541 Chapter 5 : Application to elliptic curveElliptic curveIn mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
s - 545 Appendix: Gorenstein rings and local complete intersections
Gerd Faltings
Gerd Faltings
Gerd Faltings is a German mathematician known for his work in arithmetic algebraic geometry.From 1972 to 1978, he studied mathematics and physics at the University of Münster. In 1978 he received his PhD in mathematics and in 1981 he got the venia legendi in mathematics, both from the University...
provided some simplifications to the 1995 proof, primarily in switch from geometric constructions to rather simpler algebraic ones. The book of the Cornell conference also contained simplifications to the original proof.
Culmination of the work of many
Because Wiles had incorporated the work of so many other specialists, it had been suggested in 1994 that only a small number of people were capable of fully understanding at that time all the details of what he had done. The number is likely much larger now with the 10-day conference and book organized by Cornell et al., which has done much to make the full range of required topics accessible to graduate students in number theory. The paper provides a long Bibliography and Wiles mentions the names of many mathematicians in the text. The list of some of the many other mathematicians whose work the proof incorporates includes Felix KleinFelix Klein
Christian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...
, Robert Fricke
Robert Fricke
Karl Emmanuel Robert Fricke was a German mathematician, known for his work in function theory, especially on elliptic, modular and automorphic functions...
, Adolf Hurwitz
Adolf Hurwitz
Adolf Hurwitz was a German mathematician.-Early life:He was born to a Jewish family in Hildesheim, former Kingdom of Hannover, now Lower Saxony, Germany, and died in Zürich, in Switzerland. Family records indicate that he had siblings and cousins, but their names have yet to be confirmed...
, Erich Hecke
Erich Hecke
Erich Hecke was a German mathematician. He obtained his doctorate in Göttingen under the supervision of David Hilbert. Kurt Reidemeister and Heinrich Behnke were among his students....
, Barry Mazur
Barry Mazur
-Life:Born in New York City, Mazur attended the Bronx High School of Science and MIT, although he did not graduate from the latter on account of failing a then-present ROTC requirement. Regardless, he was accepted for graduate school and received his Ph.D. from Princeton University in 1959,...
, Dirichlet
Johann Peter Gustav Lejeune Dirichlet
Johann Peter Gustav Lejeune Dirichlet was a German mathematician with deep contributions to number theory , as well as to the theory of Fourier series and other topics in mathematical analysis; he is credited with being one of the first mathematicians to give the modern formal definition of a...
, Richard Dedekind
Richard Dedekind
Julius Wilhelm Richard Dedekind was a German mathematician who did important work in abstract algebra , algebraic number theory and the foundations of the real numbers.-Life:...
, Robert Langlands
Robert Langlands
Robert Phelan Langlands is a mathematician, best known as the founder of the Langlands program. He is an emeritus professor at the Institute for Advanced Study...
, Jerrold B. Tunnell, Jun-Ichi Igusa, Martin Eichler
Martin Eichler
Martin Eichler was a German number theorist.Eichler received his Ph.D. from the Martin Luther University of Halle-Wittenberg in 1936....
, André Bloch
André Bloch (mathematician)
André Bloch was a Jewish-French mathematician who is best remembered for a result called Bloch's theorem. Bloch was institutionalized in a mental asylum for thirty-one years of his life, during which all of his mathematical output was produced.- Early life :Bloch was born in 1893 in Besançon,...
, Tosio Kato, Ernst S. Selmer, John Tate
John Tate
John Torrence Tate Jr. is an American mathematician, distinguished for many fundamental contributions in algebraic number theory, arithmetic geometry and related areas in algebraic geometry.-Biography:...
, P. Georges Poitou, Henri Carayol, Emil Artin
Emil Artin
Emil Artin was an Austrian-American mathematician of Armenian descent.-Parents:Emil Artin was born in Vienna to parents Emma Maria, née Laura , a soubrette on the operetta stages of Austria and Germany, and Emil Hadochadus Maria Artin, Austrian-born of Armenian descent...
, Jean-Marc Fontaine, Karl Rubin
Karl Rubin
Karl Rubin is an American mathematician at University of California, Irvine as Thorp Professor of Mathematics. His research interest is in elliptic curves. He was the first mathematician to show that some elliptic curves over the rationals have finite Tate-Shafarevich groups...
, Pierre Deligne
Pierre Deligne
- See also :* Deligne conjecture* Deligne–Mumford moduli space of curves* Deligne–Mumford stacks* Deligne cohomology* Fourier–Deligne transform* Langlands–Deligne local constant- External links :...
, Vladimir Drinfel'd
Vladimir Drinfel'd
Vladimir Gershonovich Drinfel'd is a Ukrainian and Soviet mathematician at the University of Chicago.The work of Drinfeld related algebraic geometry over finite fields with number theory, especially the theory of automorphic forms, through the notions of elliptic module and the theory of the...
and Haruzo Hida.
Subsequent developments
In 1998, the full modularity theorem was proven by Christophe BreuilChristophe Breuil
Christophe Breuil is a French mathematician, who works in algebraic geometry and number theory.-Academic life:Breuil attended schools in Brive-la-Gaillarde and Toulouse and studied from 1990 to 1992 at the Ecole Polytechnique....
, Brian Conrad
Brian Conrad
Brian Conrad , is an American mathematician and number theorist, working at Stanford University. Previously he was at the University of Michigan....
, Fred Diamond
Fred Diamond
Fred Diamond is an American mathematician, known for his role in proving the modularity theorem for elliptic curves. His research interest is in modular forms and Galois representations....
, and Richard Taylor
Richard Taylor (mathematician)
-External links:**...
using many of the methods that Andrew Wiles used in his 1995 published papers.
A computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
challenge given in 2005 is "Formalize and verify by computer a proof of Fermat's Last Theorem, as proved by A. Wiles in 1995."
Reading and notation guide
The Wiles paper is over 100 pages long and often uses the peculiar symbols and notations of group theoryGroup theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, commutative algebra
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
, and Galois theory
Galois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
.
One might want to first read the 1993 email of Ken Ribet, Hesselink's quick review of top-level issues gives just the elementary algebra and avoids abstract algebra., or Daney's web page which provides a set of his own notes and lists the current books available on the subject. Weston attempts to provide a handy map of some of the relationships between the subjects. F. Q. Gouvêa provides an award-winning review of some of the required topics. Faltings' 5-page technical bulletin on the matter is a quick and technical review of the proof for the non-specialist. For those in search of a commercially available book to guide them, he recommended that those familiar with abstract algebra read Hellegouarch, then read the Cornell book, which is claimed to be accessible to "a graduate student in number theory". Note that not even the Cornell book can cover the entirety of the Wiles proof.
The work of almost every mathematician who helped to lay the groundwork for Wiles did so in specialized ways, often creating new specialized concepts and yet more new jargon
Jargon
Jargon is terminology which is especially defined in relationship to a specific activity, profession, group, or event. The philosophe Condillac observed in 1782 that "Every science requires a special language because every science has its own ideas." As a rationalist member of the Enlightenment he...
. In the equations, subscripts and superscripts are used extensively because of the numbers of concepts that Wiles is sometimes dealing with in an equation.
- See the glossaries listed in Lists of mathematics topics#Pure mathematics, such as Glossary of arithmetic and Diophantine geometryGlossary of arithmetic and Diophantine geometryThis is a glossary of arithmetic and Diophantine geometry in mathematics, areas growing out of the traditional study of Diophantine equations to encompass large parts of number theory and algebraic geometry...
. Daney provides a proof-specific glossary. - See Table of mathematical symbolsTable of mathematical symbolsThis is a listing of common symbols found within all branches of mathematics. Each symbol is listed in both HTML, which depends on appropriate fonts being installed, and in , as an image.-Symbols:-Variations:...
and Table of logic symbolsTable of logic symbolsIn logic, a set of symbols is commonly used to express logical representation. As logicians are familiar with these symbols, they are not explained each time they are used. So, for students of logic, the following table lists many common symbols together with their name, pronunciation and related... - For the deformation theory, Wiles defines restrictions (or cases) on the deformations as Selmer (sel), ordinary(ord), strict(str) or flat(fl) and he uses the abbreviations list here. He usually uses these as a subscript but he occasionally uses them as a superscript. There is also a fifth case: the implied "unrestricted" case but note that the superscript "unr" is not an abbreviation for unrestricted.
- Qunr is the unramifiedRamificationIn mathematics, ramification is a geometric term used for 'branching out', in the way that the square root function, for complex numbers, can be seen to have two branches differing in sign...
extension of Q. A related but more specialized topic used is crystalline cohomologyCrystalline cohomologyIn mathematics, crystalline cohomology is a Weil cohomology theory for schemes introduced by and developed by . Its values are modules over rings of Witt vectors over the base field....
. See also Galois cohomologyGalois cohomologyIn mathematics, Galois cohomology is the study of the group cohomology of Galois modules, that is, the application of homological algebra to modules for Galois groups...
. - Some relevant named concepts: Hasse-Weil zeta functionHasse-Weil zeta functionIn mathematics, the Hasse–Weil zeta function attached to an algebraic variety V defined over an algebraic number field K is one of the two most important types of L-function. Such L-functions are called 'global', in that they are defined as Euler products in terms of local zeta functions...
, Mordell–Weil theoremMordell–Weil theoremIn mathematics, the Mordell–Weil theorem states that for an abelian variety A over a number field K, the group A of K-rational points of A is a finitely-generated abelian group, called the Mordell-Weil group...
, Deligne-Serre theorem - Grab bag of jargon mentioned in paper: coverCover (topology)In mathematics, a cover of a set X is a collection of sets whose union contains X as a subset. Formally, ifC = \lbrace U_\alpha: \alpha \in A\rbrace...
and liftLift (mathematics)In the branch of mathematics called category theory, given a morphism f from an object X to an object Y, and a morphism g from an object Z to Y, a lift of f to Z is a morphism h from X to Z such that gh = f.A basic example in topology is lifting a path in one space to a path in a covering space...
, finite fieldFinite fieldIn abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
, isomorphismIsomorphismIn abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
, surjective functionSurjective functionIn mathematics, a function f from a set X to a set Y is surjective , or a surjection, if every element y in Y has a corresponding element x in X so that f = y...
, decomposition group, j-invariantJ-invariantIn mathematics, Klein's j-invariant, regarded as a function of a complex variable τ, is a modular function defined on the upper half-plane of complex numbers.We haveThe modular discriminant \Delta is defined as \Delta=g_2^3-27g_3^2...
of elliptic curves, Abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
, Grossencharacter, L-functionL-functionThe theory of L-functions has become a very substantial, and still largely conjectural, part of contemporary analytic number theory. In it, broad generalisations of the Riemann zeta function and the L-series for a Dirichlet character are constructed, and their general properties, in most cases...
, abelian varietyAbelian varietyIn mathematics, particularly in algebraic geometry, complex analysis and number theory, an abelian variety is a projective algebraic variety that is also an algebraic group, i.e., has a group law that can be defined by regular functions...
, Jacobian, Néron modelNéron modelIn algebraic geometry, a Néron model for an abelian variety AK defined over a local field K is the "best possible" group scheme AO defined over the ring of integers R of the local field K that becomes isomorphic to AK after base change from R to K.They were introduced by André Néron...
, Gorenstein ringGorenstein ringIn commutative algebra, a Gorenstein local ring is a Noetherian commutative local ring R with finite injective dimension, as an R-module. There are many equivalent conditions, some of them listed below, most dealing with some sort of duality condition....
, Torsion subgroupTorsion subgroupIn the theory of abelian groups, the torsion subgroup AT of an abelian group A is the subgroup of A consisting of all elements that have finite order...
(including torsion points on elliptic curves here and here ), Congruence subgroupCongruence subgroupIn mathematics, a congruence subgroup of a matrix group with integer entries is a subgroup defined by congruence conditions on the entries. A very simple example would be invertible 2x2 integer matrices of determinant 1, such that the off-diagonal entries are even.An importance class of congruence...
, eigenform, Character (mathematics)Character (mathematics)In mathematics, a character is a special kind of function from a group to a field . There are at least two distinct, but overlapping meanings...
, Irreducibility (mathematics), Image (mathematics)Image (mathematics)In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
, dihedralDihedral groupIn mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
, Conductor, Lattice (group)Lattice (group)In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
, Cyclotomic fieldCyclotomic fieldIn number theory, a cyclotomic field is a number field obtained by adjoining a complex primitive root of unity to Q, the field of rational numbers...
, Cyclotomic characterCyclotomic characterIn number theory, a cyclotomic character is a character of a Galois group giving the Galois action on a group of roots of unity. As a one-dimensional representation over a ring R, its representation space is generally denoted by R .-p-adic cyclotomic character:If p is a prime, and G is the absolute...
, Splitting of prime ideals in Galois extensionsSplitting of prime ideals in Galois extensionsIn mathematics, the interplay between the Galois group G of a Galois extension L of a number field K, and the way the prime ideals P of the ring of integers OK factorise as products of prime ideals of OL, provides one of the richest parts of algebraic number theory...
(and decomposition group and inertia group), Quotient spaceQuotient spaceIn topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
, Quotient groupQuotient groupIn mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
External links
The title of one edition of the PBS television series NOVA, discusses Andrew Wiles's effort to prove Fermat's Last Theorem broadcast on BBC Horizon and UTVUTV
UTV is a television channel based in the UK region of Northern Ireland. The channel is the Channel 3 or Independent Television licensee for Northern Ireland and is operated by UTV Limited, a wholly owned subsidiary of UTV Media.- Terrestrial :* Analogue: Normally tuned to 3 * Freeview : 3...
/Documentary series as 1996
- Wiles, Ribet, Shimura-Taniyama-Weil and Fermat's Last Theorem
- Are mathematicians finally satisfied with Andrew Wiles's proof of Fermat's Last Theorem? Why has this theorem been so difficult to prove?, Scientific AmericanScientific AmericanScientific American is a popular science magazine. It is notable for its long history of presenting science monthly to an educated but not necessarily scientific public, through its careful attention to the clarity of its text as well as the quality of its specially commissioned color graphics...
, October 21, 1999