
Serre conjecture (number theory)
Encyclopedia
In mathematics
, Jean-Pierre Serre
conjectured the following result regarding two-dimensional Galois representations. This was a significant step in number theory
, though this was not realised for at least a decade.
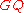 of the rational number field
of the rational number field 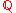 .
.
Let be an absolutely irreducible
be an absolutely irreducible
, continuous, and odd two-dimensional representation of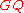 over a finite field
over a finite field

of characteristic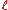 ,
,

To any normalized modular eigenform

of level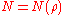 , weight
, weight 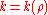 , and some Nebentype character
, and some Nebentype character
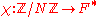 ,
,
a theorem due to Shimura, Deligne, and Serre-Deligne attaches to a representation
a representation
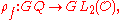
where is the ring of integers in a finite extension of
is the ring of integers in a finite extension of 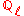 . This representation is characterized by the condition that for all prime numbers
. This representation is characterized by the condition that for all prime numbers 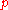 , coprime
, coprime
to we have
we have

and
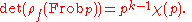
Reducing this representation modulo the maximal ideal of gives a mod
gives a mod 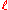 representation
representation 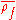 of
of 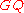 .
.
Serre's conjecture asserts that for any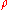 as above, there is a modular eigenform
as above, there is a modular eigenform  such that
such that
 .
.
The level and weight of the conjectural form are explicitly calculated in Serre's article. In addition, he derives a number of results from this conjecture, among them Fermat's Last Theorem
are explicitly calculated in Serre's article. In addition, he derives a number of results from this conjecture, among them Fermat's Last Theorem
and the now-proven Taniyama-Weil (or Taniyama-Shimura) conjecture, now known as the Modularity Theorem (although this implies Fermat's Last Theorem, Serre proves it directly from his conjecture).
and Jean-Pierre Wintenberger
, and by Luis Dieulefait, independently.
In 2005, Chandrashekhar Khare obtained a proof of the level 1 case of Serre conjecture, and in 2008 a proof of the full conjecture in collaboration with Jean-Pierre Wintenberger.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Jean-Pierre Serre
Jean-Pierre Serre
Jean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...
conjectured the following result regarding two-dimensional Galois representations. This was a significant step in number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, though this was not realised for at least a decade.
Formulation
The conjecture concerns the absolute Galois groupAbsolute Galois group
In mathematics, the absolute Galois group GK of a field K is the Galois group of Ksep over K, where Ksep is a separable closure of K. Alternatively it is the group of all automorphisms of the algebraic closure of K that fix K. The absolute Galois group is unique up to isomorphism...
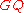 of the rational number field
of the rational number field 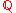 .
.Let
 be an absolutely irreducible
be an absolutely irreducibleAbsolutely irreducible
In mathematics, absolutely irreducible is a term applied to linear representations or algebraic varieties over a field. It means that the object in question remains irreducible, even after any finite extension of the field of coefficients...
, continuous, and odd two-dimensional representation of
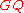 over a finite field
over a finite field
of characteristic
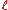 ,
,
To any normalized modular eigenform

of level
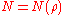 , weight
, weight 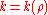 , and some Nebentype character
, and some Nebentype character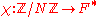 ,
,a theorem due to Shimura, Deligne, and Serre-Deligne attaches to
 a representation
a representation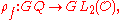
where
 is the ring of integers in a finite extension of
is the ring of integers in a finite extension of 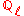 . This representation is characterized by the condition that for all prime numbers
. This representation is characterized by the condition that for all prime numbers 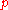 , coprime
, coprimeCoprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
to
 we have
we have
and
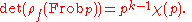
Reducing this representation modulo the maximal ideal of
 gives a mod
gives a mod 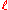 representation
representation 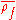 of
of 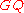 .
.Serre's conjecture asserts that for any
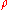 as above, there is a modular eigenform
as above, there is a modular eigenform  such that
such that .
.The level and weight of the conjectural form
 are explicitly calculated in Serre's article. In addition, he derives a number of results from this conjecture, among them Fermat's Last Theorem
are explicitly calculated in Serre's article. In addition, he derives a number of results from this conjecture, among them Fermat's Last TheoremFermat's Last Theorem
In number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
and the now-proven Taniyama-Weil (or Taniyama-Shimura) conjecture, now known as the Modularity Theorem (although this implies Fermat's Last Theorem, Serre proves it directly from his conjecture).
Proof
A proof of the level 1 and small weight cases of the conjecture was obtained during 2004 by Chandrashekhar KhareChandrashekhar Khare
Chandrashekhar B. Khare is a professor of mathematics at the University of California Los Angeles. In 2005, he made a major advance in the field of Galois representations and number theory by proving the level 1 Serre conjecture, and later a proof of the full conjecture with Jean-Pierre Wintenberger...
and Jean-Pierre Wintenberger
Jean-Pierre Wintenberger
Jean-Pierre Wintenberger is a French mathematician, and currently a professor of mathematics at the University of Strasbourg. He was corecipient of the 2011 Cole Prize in number theory, along with Chandrashekhar Khare, for his proof of Serre's modularity conjecture.Wintenberger earned his Ph.D. at...
, and by Luis Dieulefait, independently.
In 2005, Chandrashekhar Khare obtained a proof of the level 1 case of Serre conjecture, and in 2008 a proof of the full conjecture in collaboration with Jean-Pierre Wintenberger.
External links
- Serre's Modularity Conjecture 50 minute lecture by Ken Ribet given on October 25, 2007 ( slides PDF , other version of slides PDF)
- Lectures on Serre's conjectures

