Shimura–Taniyama theorem
Encyclopedia
In mathematics the modularity theorem (formerly called the Taniyama–Shimura–Weil conjecture and several related names) states that elliptic curve
s over the field of rational number
s are related to modular form
s. Andrew Wiles
proved the modularity theorem for semistable elliptic curves, which was enough to imply Fermat's last theorem
, and Christophe Breuil
, Brian Conrad
, Fred Diamond
, and Richard Taylor
extended his techniques to prove the full modularity theorem in 2001.
The modularity theorem is a special case of more general conjectures due to Robert Langlands
. The Langlands program
seeks to attach an automorphic form
or automorphic representation (a suitable generalization of a modular form) to more general objects of arithmetic algebraic geometry, such as to every elliptic curve over a number field. Most cases of these extended conjectures have not yet been proved.
states that any elliptic curve
over Q can be obtained via a rational map with integer
coefficient
s from the classical modular curve
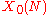
for some integer N; this is a curve with integer coefficients with an explicit definition. This mapping is called a modular parametrization of level N. If N is the smallest integer for which such a parametrization can be found (which by the modularity theorem itself is now known to be a number called the conductor), then the parametrization may be defined in terms of a mapping generated by a particular kind of modular form of weight two and level N, a normalized newform with integer q-expansion, followed if need be by an isogeny.
The modularity theorem implies a closely related analytic statement: to an elliptic curve E over Q we may attach a corresponding L-series. The L-series is a Dirichlet series, commonly written
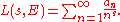
The generating function
of the coefficients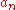
is then
If we make the substitution
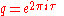
we see that we have written the Fourier expansion
of a function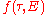
of the complex variable τ, so the coefficients of the q-series are also thought of as the Fourier coefficients of 
. The function obtained in this way is, remarkably, a cusp form
of weight two and level N and is also an eigenform (an eigenvector of all Hecke operator
s); this is the Hasse–Weil conjecture, which follows from the modularity theorem.
Some modular forms of weight two, in turn, correspond to holomorphic differentials for an elliptic curve. The Jacobian of the modular curve can (up to isogeny) be written as a product of irreducible Abelian varieties, corresponding to Hecke eigenforms of weight 2. The 1-dimensional factors are elliptic curves (there can also be higher dimensional factors, so not all Hecke eigenforms correspond to rational elliptic curves). The curve obtained by finding the corresponding cusp form, and then constructing a curve from it, is isogenous to the original curve (but not, in general, isomorphic to it).
and Taniyama worked on improving its rigor until 1957. rediscovered the conjecture, and showed that it would follow from the (conjectured) functional equations for some twisted L-series of the elliptic curve; this was the first serious evidence that the conjecture might be true. Weil also showed that the conductor of the elliptic curve should be the level of the corresponding modular form.
The conjecture attracted considerable interest when suggested that the Taniyama–Shimura–Weil conjecture implies Fermat's Last Theorem
. He did this by attempting to show that any counterexample to Fermat's Last Theorem would give rise to a non-modular elliptic curve. However, his argument was not complete. The extra condition which was needed to link Taniyama-Shimura-Weil to Fermat's Last Theorem was identified by and became known as the epsilon conjecture. In the summer of 1986, proved the epsilon conjecture, thereby proving that the Taniyama–Shimura–Weil conjecture implied Fermat's Last Theorem. , with some help from Richard Taylor
, proved the Taniyama–Shimura–Weil conjecture for all semistable elliptic curve
s, which was strong enough to yield a proof of Fermat's Last Theorem.
The full Taniyama–Shimura–Weil conjecture was finally proved by , , and who, building on Wiles' work, incrementally chipped away at the remaining cases until the full result was proved. The now fully proved conjecture became known as the modularity theorem.
Several theorems in number theory similar to Fermat's Last Theorem follow from the modularity theorem. For example: no cube can be written as a sum of two coprime
n-th powers, n ≥ 3. (The case n = 3 was already known by Euler.)
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
s over the field of rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s are related to modular form
Modular form
In mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...
s. Andrew Wiles
Andrew Wiles
Sir Andrew John Wiles KBE FRS is a British mathematician and a Royal Society Research Professor at Oxford University, specializing in number theory...
proved the modularity theorem for semistable elliptic curves, which was enough to imply Fermat's last theorem
Fermat's Last Theorem
In number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
, and Christophe Breuil
Christophe Breuil
Christophe Breuil is a French mathematician, who works in algebraic geometry and number theory.-Academic life:Breuil attended schools in Brive-la-Gaillarde and Toulouse and studied from 1990 to 1992 at the Ecole Polytechnique....
, Brian Conrad
Brian Conrad
Brian Conrad , is an American mathematician and number theorist, working at Stanford University. Previously he was at the University of Michigan....
, Fred Diamond
Fred Diamond
Fred Diamond is an American mathematician, known for his role in proving the modularity theorem for elliptic curves. His research interest is in modular forms and Galois representations....
, and Richard Taylor
Richard Taylor (mathematician)
-External links:**...
extended his techniques to prove the full modularity theorem in 2001.
The modularity theorem is a special case of more general conjectures due to Robert Langlands
Robert Langlands
Robert Phelan Langlands is a mathematician, best known as the founder of the Langlands program. He is an emeritus professor at the Institute for Advanced Study...
. The Langlands program
Langlands program
The Langlands program is a web of far-reaching and influential conjectures that relate Galois groups in algebraic number theory to automorphic forms and representation theory of algebraic groups over local fields and adeles. It was proposed by ....
seeks to attach an automorphic form
Automorphic form
In mathematics, the general notion of automorphic form is the extension to analytic functions, perhaps of several complex variables, of the theory of modular forms...
or automorphic representation (a suitable generalization of a modular form) to more general objects of arithmetic algebraic geometry, such as to every elliptic curve over a number field. Most cases of these extended conjectures have not yet been proved.
Statement
The theoremTheorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
states that any elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
over Q can be obtained via a rational map with integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s from the classical modular curve
Classical modular curve
In number theory, the classical modular curve is an irreducible plane algebraic curve given by an equationwhere for the j-invariant j,is a point on the curve. The curve is sometimes called X0, though often that is used for the abstract algebraic curve for which there exist various models...
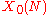
for some integer N; this is a curve with integer coefficients with an explicit definition. This mapping is called a modular parametrization of level N. If N is the smallest integer for which such a parametrization can be found (which by the modularity theorem itself is now known to be a number called the conductor), then the parametrization may be defined in terms of a mapping generated by a particular kind of modular form of weight two and level N, a normalized newform with integer q-expansion, followed if need be by an isogeny.
The modularity theorem implies a closely related analytic statement: to an elliptic curve E over Q we may attach a corresponding L-series. The L-series is a Dirichlet series, commonly written
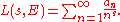
The generating function
Generating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
of the coefficients
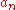is thenIf we make the substitution
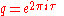
we see that we have written the Fourier expansion
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
of a function
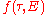of the complex variable τ, so the coefficients of the q-series are also thought of as the Fourier coefficients of . The function obtained in this way is, remarkably, a cusp formModular form
In mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...
of weight two and level N and is also an eigenform (an eigenvector of all Hecke operator
Hecke operator
In mathematics, in particular in the theory of modular forms, a Hecke operator, studied by , is a certain kind of "averaging" operator that plays a significant role in the structure of vector spaces of modular forms and more general automorphic representations....
s); this is the Hasse–Weil conjecture, which follows from the modularity theorem.
Some modular forms of weight two, in turn, correspond to holomorphic differentials for an elliptic curve. The Jacobian of the modular curve can (up to isogeny) be written as a product of irreducible Abelian varieties, corresponding to Hecke eigenforms of weight 2. The 1-dimensional factors are elliptic curves (there can also be higher dimensional factors, so not all Hecke eigenforms correspond to rational elliptic curves). The curve obtained by finding the corresponding cusp form, and then constructing a curve from it, is isogenous to the original curve (but not, in general, isomorphic to it).
History
stated a preliminary (slightly incorrect) version of the conjecture at the 1955 international symposium on algebraic number theory in Tokyo and Nikko. Goro ShimuraGoro Shimura
is a Japanese mathematician, and currently a professor emeritus of mathematics at Princeton University.Shimura was a colleague and a friend of Yutaka Taniyama...
and Taniyama worked on improving its rigor until 1957. rediscovered the conjecture, and showed that it would follow from the (conjectured) functional equations for some twisted L-series of the elliptic curve; this was the first serious evidence that the conjecture might be true. Weil also showed that the conductor of the elliptic curve should be the level of the corresponding modular form.
The conjecture attracted considerable interest when suggested that the Taniyama–Shimura–Weil conjecture implies Fermat's Last Theorem
Fermat's Last Theorem
In number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
. He did this by attempting to show that any counterexample to Fermat's Last Theorem would give rise to a non-modular elliptic curve. However, his argument was not complete. The extra condition which was needed to link Taniyama-Shimura-Weil to Fermat's Last Theorem was identified by and became known as the epsilon conjecture. In the summer of 1986, proved the epsilon conjecture, thereby proving that the Taniyama–Shimura–Weil conjecture implied Fermat's Last Theorem. , with some help from Richard Taylor
Richard Taylor (mathematician)
-External links:**...
, proved the Taniyama–Shimura–Weil conjecture for all semistable elliptic curve
Semistable elliptic curve
In algebraic geometry, a semistable abelian variety is an abelian variety defined over a global or local field, which is characterized by how it reduces at the primes of the field....
s, which was strong enough to yield a proof of Fermat's Last Theorem.
The full Taniyama–Shimura–Weil conjecture was finally proved by , , and who, building on Wiles' work, incrementally chipped away at the remaining cases until the full result was proved. The now fully proved conjecture became known as the modularity theorem.
Several theorems in number theory similar to Fermat's Last Theorem follow from the modularity theorem. For example: no cube can be written as a sum of two coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
n-th powers, n ≥ 3. (The case n = 3 was already known by Euler.)