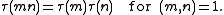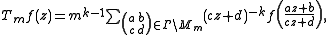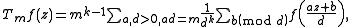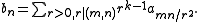Hecke operator
Encyclopedia
In mathematics
, in particular in the theory of modular form
s, a Hecke operator, studied by , is a certain kind of "averaging" operator that plays a significant role in the structure of vector space
s of modular forms and more general automorphic representations.
of Ramanujan, ahead of the general theory given by . Mordell proved that the Ramanujan tau function, expressing the coefficients of the Ramanujan form,
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in particular in the theory of modular form
Modular form
In mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...
s, a Hecke operator, studied by , is a certain kind of "averaging" operator that plays a significant role in the structure of vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s of modular forms and more general automorphic representations.
History
used Hecke operators on modular forms in a paper on the special cusp formCusp form
In number theory, a branch of mathematics, a cusp form is a particular kind of modular form, distinguished in the case of modular forms for the modular group by the vanishing in the Fourier series expansion \Sigma a_n q^n...
of Ramanujan, ahead of the general theory given by . Mordell proved that the Ramanujan tau function, expressing the coefficients of the Ramanujan form,
-
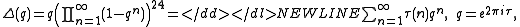
is a multiplicative functionMultiplicative functionIn number theory, a multiplicative function is an arithmetic function f of the positive integer n with the property that f = 1 and whenevera and b are coprime, then...
:
The idea goes back to earlier work of HurwitzHurwitzHurwitz is a surname and may refer to:*Aaron Hurwitz, musician, see Live on Breeze Hill*Adolf Hurwitz , German mathematician**Hurwitz polynomial**Hurwitz matrix**Hurwitz quaternion**Hurwitz's automorphisms theorem**Hurwitz zeta function...
, who treated algebraic correspondenceCorrespondence (mathematics)In mathematics and mathematical economics, correspondence is a term with several related but not identical meanings.* In general mathematics, correspondence is an alternative term for a relation between two sets...
s between modular curveModular curveIn number theory and algebraic geometry, a modular curve Y is a Riemann surface, or the corresponding algebraic curve, constructed as a quotient of the complex upper half-plane H by the action of a congruence subgroup Γ of the modular group of integral 2×2 matrices SL...
s which realise some individual Hecke operators.
Mathematical description
Hecke operators can be realised in a number of contexts. The simplest meaning is combinatorial, namely as taking for a given integer n some function f(Λ) defined on the latticeLattice (group)In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
s of fixed rank to
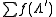
with the sum taken over all the Λ′ that are subgroupSubgroupIn group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s of Λ of index n. For example, with n=2 and two dimensions, there are three such Λ′. Modular formModular formIn mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...
s are particular kinds of functions of a lattice, subject to conditions making them analytic functionAnalytic functionIn mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
s and homogeneousHomogeneous functionIn mathematics, a homogeneous function is a function with multiplicative scaling behaviour: if the argument is multiplied by a factor, then the result is multiplied by some power of this factor. More precisely, if is a function between two vector spaces over a field F, and k is an integer, then...
with respect to homotheties, as well as moderate growth at infinity; these conditions are preserved by the summation, and so Hecke operators preserve the space of modular forms of a given weight.
Another way to express Hecke operators is by means of double cosetDouble cosetIn mathematics, an double coset in G, where G is a group and H and K are subgroups of G, is an equivalence class for the equivalence relation defined on G by...
s in the modular groupModular groupIn mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
. In the contemporary adelic approach, this translates to double cosets with respect to some compact subgroups.
Explicit formula
Let Mm be the set of 2×2 integral matrices with determinantDeterminantIn linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
m and Γ = M1 be the full modular groupModular groupIn mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
SL(2, Z). Given a modular form f(z) of weight k, the mth Hecke operator acts by the formula
where z is in the upper half-plane and the normalization constant mk−1 assures that the image of a form with integer Fourier coefficients has integer Fourier coefficients. This can be rewritten in the form
which leads to the formula for the Fourier coefficients of Tmf(z) = ∑ bnqn in terms of the Fourier coefficients of f(z) = ∑ anqn:
One can see from this explicit formula that Hecke operators with different indices commute and that if a0 = 0 then b0 = 0, so the subspace Sk of cusp forms of weight k is preserved by the Hecke operators. If a (non-zero) cusp form f is a simultaneous eigenformEigenformAn eigenform is a modular form which is an eigenvector for all Hecke operators Tm, m = 1, 2, 3, …....
of all Hecke operators Tm with eigenvalues λm then am = λma1 and a1 ≠ 0. Hecke eigenforms are normalized so that a1 = 1, then
Thus for normalized cuspidal Hecke eigenforms of integer weight, their Fourier coefficients coincide with their Hecke eigenvalues.
Hecke algebras
Algebras of Hecke operators are called Hecke algebras, and are commutative ringCommutative ringIn ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
s. Other, related, mathematical rings are called Hecke algebras, although the link to Hecke operators is not entirely obvious. These algebras include certain quotients of the group algebraGroup algebraIn mathematics, the group algebra is any of various constructions to assign to a locally compact group an operator algebra , such that representations of the algebra are related to representations of the group...
s of braid groupBraid groupIn mathematics, the braid group on n strands, denoted by Bn, is a group which has an intuitive geometrical representation, and in a sense generalizes the symmetric group Sn. Here, n is a natural number; if n > 1, then Bn is an infinite group...
s. The presence of this commutative operator algebra plays a significant role in the harmonic analysisHarmonic analysisHarmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
of modular forms and generalisations. In the classical elliptic modular form theory, the Hecke operators Tn with n coprime to the level acting on the space of cusp forms of a given weight are self-adjointSelf-adjoint operatorIn mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
with respect to the Petersson inner product. Therefore, the spectral theoremSpectral theoremIn mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
implies that there is a basis of modular forms that are eigenfunctionEigenfunctionIn mathematics, an eigenfunction of a linear operator, A, defined on some function space is any non-zero function f in that space that returns from the operator exactly as is, except for a multiplicative scaling factor. More precisely, one has...
s for these Hecke operators. Each of these basic forms possesses an Euler productEuler productIn number theory, an Euler product is an expansion of a Dirichlet series into an infinite product indexed by prime numbers. The name arose from the case of the Riemann zeta-function, where such a product representation was proved by Leonhard Euler.-Definition:...
. More precisely, its Mellin transformMellin transformIn mathematics, the Mellin transform is an integral transform that may be regarded as the multiplicative version of the two-sided Laplace transform...
is Dirichlet series that has Euler productEuler productIn number theory, an Euler product is an expansion of a Dirichlet series into an infinite product indexed by prime numbers. The name arose from the case of the Riemann zeta-function, where such a product representation was proved by Leonhard Euler.-Definition:...
s with the local factor for each prime p is the inverse of the Hecke polynomial, a quadratic polynomial in p−s. In the case treated by Mordell, the space of cusp forms of weight 12 with respect to the full modular group is one-dimensional. It follows that the Ramanujan form has an Euler product and establishes the multiplicativity of τ(n). -