
Generator (category theory)
Encyclopedia
In category theory
in mathematics
a generator (or separator) of a category
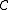 is an object G of the category, such that for any two different morphisms
is an object G of the category, such that for any two different morphisms  in
in 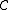 , there is a morphism
, there is a morphism 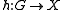 , such that the compositions
, such that the compositions 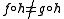 .
.
Generators are central to the definition of Grothendieck categories
.
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
in mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
a generator (or separator) of a category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
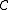 is an object G of the category, such that for any two different morphisms
is an object G of the category, such that for any two different morphisms  in
in 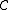 , there is a morphism
, there is a morphism 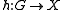 , such that the compositions
, such that the compositions 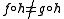 .
.Generators are central to the definition of Grothendieck categories
Grothendieck category
In mathematics, a Grothendieck category is an AB5 category with a generator. In other words, it is an abelian category A admitting arbitrary coproducts, for which filtered colimits of exact sequences are exact and which possess a generator, i.e...
.
Examples
- In the category of abelian groups, the group of integers
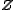 is a generator: If f and g are different, then there is an element
is a generator: If f and g are different, then there is an element 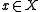 , such that
, such that 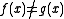 . Hence the map
. Hence the map 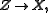
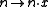 suffices.
suffices. - Similarly, the one-point set is a generator for the category of sets.
External links
- Generator in nLab

