Yoneda lemma
Encyclopedia
In mathematics
, specifically in category theory
, the Yoneda lemma is an abstract result on functor
s of the type morphisms into a fixed object. It is a vast generalisation of Cayley's theorem
from group theory
(viewing a group as a particular kind of category with just one object). It allows the embedding of any category into a category of functors (contravariant set-valued functors) defined on that category. It also clarifies how the embedded category, of representable functor
s and their natural transformation
s, relates to the other objects in the larger functor category. It is an important tool that underlies several modern developments in algebraic geometry
and representation theory
. It is named after Nobuo Yoneda
.
with function
s as morphism
s). Set is a category we understand well, and a functor of C into Set can be seen as a "representation" of C in terms of known structures. The original category C is contained in this functor category, but new objects appear in the functor category which were absent and "hidden" in C. Treating these new objects just like the old ones often unifies and simplifies the theory.
This approach is akin to (and in fact generalizes) the common method of studying a ring
by investigating the modules
over that ring. The ring takes the place of the category C, and the category of modules over the ring is a category of functors defined on C.
, Set. If C is a locally small category (i.e. the hom-sets are actual sets and not proper classes), then each object A of C gives rise to a natural functor to Set called a hom-functor. This functor is denoted:
The (covariant) hom-functor hA sends X to the set of morphism
s Hom(A,X) and sends a morphism f from X to Y to the morphism f o – (composition with f on the left) that sends a morphism g in Hom(A,X) to the morphism f o g in Hom(A,Y).
Let F be an arbitrary functor from C to Set. Then Yoneda's lemma says that:
for each object A of C, the natural transformation
s from hA to F are in one-to-one correspondence with the elements of F(A). That is,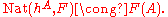
Moreover this isomorphism is natural in A and F when both sides are regarded as functors from SetC to Set.
Given a natural transformation Φ from hA to F, the corresponding element of F(A) is
.
There is a contravariant version of Yoneda's lemma which concerns contravariant functors from C to Set. This version involves the contravariant hom-functor
which sends X to the hom-set Hom(X,A). Given an arbitrary contravariant functor G from C to Set, Yoneda's lemma asserts that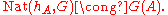
foundational EGA
use the convention in this article.
The mnemonic "falling into something" can be helpful in remembering that "hA" is the contravariant hom-functor. When the letter "A" is falling (i.e. a subscript), hA assigns to an object X the morphisms from X into A.
:
This diagram shows that the natural transformation Φ is completely determined by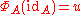
since for each morphism f : A → X one has
Moreover, any element u∈F(A) defines a natural transformation in this way. The proof in the contravariant case is completely analogous.
In this way, Yoneda's Lemma provides a complete classification of all natural transformations from the functor Hom(A,-) to an arbitrary functor F:C→Set.
That is, natural transformations between hom-functors are in one-to-one correspondence with morphisms (in the reverse direction) between the associated objects. Given a morphism f : B → A the associated natural transformation is denoted Hom(f,–).
Mapping each object A in C to its associated hom-functor hA = Hom(A,–) and each morphism f : B → A to the corresponding natural transformation Hom(f,–) determines a contravariant functor h– from C to SetC, the functor category
of all (covariant) functors from C to Set. One can interpret h– as a covariant functor: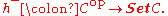
The meaning of Yoneda's lemma in this setting is that the functor h– is fully faithful
, and therefore gives an embedding of Cop in the category of functors to Set. The collection of all functors {hA, A in C} is a subcategory of SetC. Therefore, Yoneda embedding implies that the category Cop is isomorphic to the category {hA, A in C}.
The contravariant version of Yoneda's lemma states that
Therefore, h– gives rise to a covariant functor from C to the category of contravariant functors to Set: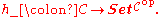
Yoneda's lemma then states that any locally small category C can be embedded in the category of contravariant functors from C to Set via h–. This is called the Yoneda embedding.
is a category where the morphism sets form abelian group
s and the composition of morphisms is bilinear
; examples are categories of abelian groups or modules. In a preadditive category, there is both a "multiplication" and an "addition" of morphisms, which is why preadditive categories are viewed as generalizations of ring
s. Rings are preadditive categories with one object.
The Yoneda lemma remains true for preadditive categories if we choose as our extension the category of additive contravariant functors from the original category into the category of abelian groups; these are functors which are compatible with the addition of morphisms and should be thought of as forming a module category over the original category. The Yoneda lemma then yields the natural procedure to enlarge a preadditive category so that the enlarged version remains preadditive — in fact, the enlarged version is an abelian category
, a much more powerful condition. In the case of a ring R, the extended category is the category of all left modules
over R, and the statement of the Yoneda lemma reduces to the well-known isomorphism
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically in category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, the Yoneda lemma is an abstract result on functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
s of the type morphisms into a fixed object. It is a vast generalisation of Cayley's theorem
Cayley's theorem
In group theory, Cayley's theorem, named in honor of Arthur Cayley, states that every group G is isomorphic to a subgroup of the symmetric group acting on G...
from group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
(viewing a group as a particular kind of category with just one object). It allows the embedding of any category into a category of functors (contravariant set-valued functors) defined on that category. It also clarifies how the embedded category, of representable functor
Representable functor
In mathematics, particularly category theory, a representable functor is a functor of a special form from an arbitrary category into the category of sets. Such functors give representations of an abstract category in terms of known structures In mathematics, particularly category theory, a...
s and their natural transformation
Natural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
s, relates to the other objects in the larger functor category. It is an important tool that underlies several modern developments in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
and representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
. It is named after Nobuo Yoneda
Nobuo Yoneda
was a Japanese mathematician and computer scientist. The Yoneda lemma in category theory is named after him. In computer science, he is known for his work on ALGOL dialects.-References:...
.
Generalities
The Yoneda lemma suggests that instead of studying the (locally small) category C, one should study the category of all functors of C into Set (the category of setsCategory of sets
In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
with function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s as morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s). Set is a category we understand well, and a functor of C into Set can be seen as a "representation" of C in terms of known structures. The original category C is contained in this functor category, but new objects appear in the functor category which were absent and "hidden" in C. Treating these new objects just like the old ones often unifies and simplifies the theory.
This approach is akin to (and in fact generalizes) the common method of studying a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
by investigating the modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
over that ring. The ring takes the place of the category C, and the category of modules over the ring is a category of functors defined on C.
General version
Yoneda's lemma concerns functors from a fixed category C to the category of setsCategory of sets
In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
, Set. If C is a locally small category (i.e. the hom-sets are actual sets and not proper classes), then each object A of C gives rise to a natural functor to Set called a hom-functor. This functor is denoted:
The (covariant) hom-functor hA sends X to the set of morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s Hom(A,X) and sends a morphism f from X to Y to the morphism f o – (composition with f on the left) that sends a morphism g in Hom(A,X) to the morphism f o g in Hom(A,Y).
Let F be an arbitrary functor from C to Set. Then Yoneda's lemma says that:
for each object A of C, the natural transformation
Natural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
s from hA to F are in one-to-one correspondence with the elements of F(A). That is,
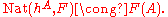
Moreover this isomorphism is natural in A and F when both sides are regarded as functors from SetC to Set.
Given a natural transformation Φ from hA to F, the corresponding element of F(A) is
.There is a contravariant version of Yoneda's lemma which concerns contravariant functors from C to Set. This version involves the contravariant hom-functor
which sends X to the hom-set Hom(X,A). Given an arbitrary contravariant functor G from C to Set, Yoneda's lemma asserts that
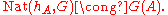
Naming conventions
The use of "hA" for the covariant hom-functor and "hA" for the contravariant hom-functor is not completely standard. Many texts and articles either use the opposite convention or completely unrelated symbols for these two functors. However, most modern algebraic geometry texts starting with Alexander Grothendieck'sAlexander Grothendieck
Alexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
foundational EGA
Éléments de géométrie algébrique
The Éléments de géométrie algébrique by Alexander Grothendieck , or EGA for short, is a rigorous treatise, in French, on algebraic geometry that was published from 1960 through 1967 by the Institut des Hautes Études Scientifiques...
use the convention in this article.
The mnemonic "falling into something" can be helpful in remembering that "hA" is the contravariant hom-functor. When the letter "A" is falling (i.e. a subscript), hA assigns to an object X the morphisms from X into A.
Proof
The proof of Yoneda's lemma is indicated by the following commutative diagramCommutative diagram
In mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
:
This diagram shows that the natural transformation Φ is completely determined by
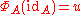since for each morphism f : A → X one hasMoreover, any element u∈F(A) defines a natural transformation in this way. The proof in the contravariant case is completely analogous.
In this way, Yoneda's Lemma provides a complete classification of all natural transformations from the functor Hom(A,-) to an arbitrary functor F:C→Set.
The Yoneda embedding
An important special case of Yoneda's lemma is when the functor F from C to Set is another hom-functor hB. In this case, the covariant version of Yoneda's lemma states thatThat is, natural transformations between hom-functors are in one-to-one correspondence with morphisms (in the reverse direction) between the associated objects. Given a morphism f : B → A the associated natural transformation is denoted Hom(f,–).
Mapping each object A in C to its associated hom-functor hA = Hom(A,–) and each morphism f : B → A to the corresponding natural transformation Hom(f,–) determines a contravariant functor h– from C to SetC, the functor category
Functor category
In category theory, a branch of mathematics, the functors between two given categories form a category, where the objects are the functors and the morphisms are natural transformations between the functors...
of all (covariant) functors from C to Set. One can interpret h– as a covariant functor:
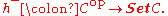
The meaning of Yoneda's lemma in this setting is that the functor h– is fully faithful
Full and faithful functors
In category theory, a faithful functor is a functor which is injective when restricted to each set of morphisms that have a given source and target....
, and therefore gives an embedding of Cop in the category of functors to Set. The collection of all functors {hA, A in C} is a subcategory of SetC. Therefore, Yoneda embedding implies that the category Cop is isomorphic to the category {hA, A in C}.
The contravariant version of Yoneda's lemma states that
Therefore, h– gives rise to a covariant functor from C to the category of contravariant functors to Set:
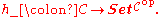
Yoneda's lemma then states that any locally small category C can be embedded in the category of contravariant functors from C to Set via h–. This is called the Yoneda embedding.
Preadditive categories, rings and modules
A preadditive categoryPreadditive category
In mathematics, specifically in category theory, a preadditive category is a category that is enriched over the monoidal category of abelian groups...
is a category where the morphism sets form abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s and the composition of morphisms is bilinear
Bilinear operator
In mathematics, a bilinear operator is a function combining elements of two vector spaces to yield an element of a third vector space that is linear in each of its arguments. Matrix multiplication is an example.-Definition:...
; examples are categories of abelian groups or modules. In a preadditive category, there is both a "multiplication" and an "addition" of morphisms, which is why preadditive categories are viewed as generalizations of ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
s. Rings are preadditive categories with one object.
The Yoneda lemma remains true for preadditive categories if we choose as our extension the category of additive contravariant functors from the original category into the category of abelian groups; these are functors which are compatible with the addition of morphisms and should be thought of as forming a module category over the original category. The Yoneda lemma then yields the natural procedure to enlarge a preadditive category so that the enlarged version remains preadditive — in fact, the enlarged version is an abelian category
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
, a much more powerful condition. In the case of a ring R, the extended category is the category of all left modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
over R, and the statement of the Yoneda lemma reduces to the well-known isomorphism
- M ≅ HomR(R,M) for all left modules M over R.