Subobject classifier
Encyclopedia
In category theory
, a subobject classifier is a special object Ω of a category; intuitively, the subobject
s of an object X correspond to the morphisms from X to Ω. As the name suggests, what a subobject classifier does is to identify/classify subobjects of a given object according to which elements belong to the subobject in question. Because of this role, the subobject classifier is also referred to as the "truth value object". In fact the way in which the subobject classifier classifies subobjects of a given object, is by assigning the values true to elements belonging to the subobject in question, and false to elements not belonging to the subobject. This is why the subobject classifier is widely used in the categorical description of logic.
and functions: to every subset j : U → X we can assign the function χj from X to Ω that maps precisely the elements of U to 1 (see characteristic function). Every function from X to Ω arises in this fashion from precisely one subset U.
To render this example more clear let us consider a subset
A of S (A ⊆ S), where S is a set. The notion of being a subset can be expressed mathematically using the so-called characteristic function χA : S → {0,1}, which is defined as follows: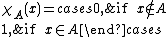
(Here we interpret 1 as true and 0 as false.) The role of the characteristic function is to determine which elements belong or not to a certain subset. Since in any category subobjects are identified as monic arrows
, we identify the value true with the arrow: true: {0} → {0, 1} which maps 0 to 1. Given this definition it can be easily seen that the subset A can be uniquely defined through the characteristic function A = χA−1(1). Therefore the diagram
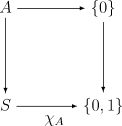
is a pullback
.
The above example of subobject classifier in Set is very useful because it enables us to easily prove the following axiom:
Axiom: Given a category C, then there exists an isomorphism
,
In Set this axiom can be restated as follows:
Axiom: The collection of all subsets of S denoted by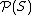
, and the collection of all maps from S to the set {0, 1} = 2 denoted by 2S are isomorphic i.e. the function 
, which in terms of single elements of 
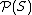is A → χA, is a bijection
.
The above axiom implies the alternative definition of a subobject classifier:
Definition: Ω is a subobject classifier iff there is a one to one correspondence between subobjects of X and morphisms from X to Ω.
with the following property:
The morphism χ j is then called the classifying morphism for the subobject represented by j.
has a subobject classifier. For the topos of sheaves
of sets on a topological space
X, it can be described in these terms: For any open set
U of X,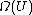
is the set of all open subsets of U. Roughly speaking an assertion inside this topos is variably true or false, and its truth value from the viewpoint of an open subset U is the open subset of U where the assertion is true.
For a small category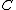
, the subobject classifer in the topos of presheaves 
is given as follows. For any 
, 
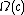is the set of sieves
on
.
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, a subobject classifier is a special object Ω of a category; intuitively, the subobject
Subobject
In category theory, a branch of mathematics, a subobject is, roughly speaking, an object which sits inside another object in the same category. The notion is a generalization of the older concepts of subset from set theory and subgroup from group theory...
s of an object X correspond to the morphisms from X to Ω. As the name suggests, what a subobject classifier does is to identify/classify subobjects of a given object according to which elements belong to the subobject in question. Because of this role, the subobject classifier is also referred to as the "truth value object". In fact the way in which the subobject classifier classifies subobjects of a given object, is by assigning the values true to elements belonging to the subobject in question, and false to elements not belonging to the subobject. This is why the subobject classifier is widely used in the categorical description of logic.
Introductory example
As an example, the set Ω = {0,1} is a subobject classifier in the category of setsCategory of sets
In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
and functions: to every subset j : U → X we can assign the function χj from X to Ω that maps precisely the elements of U to 1 (see characteristic function). Every function from X to Ω arises in this fashion from precisely one subset U.
To render this example more clear let us consider a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
A of S (A ⊆ S), where S is a set. The notion of being a subset can be expressed mathematically using the so-called characteristic function χA : S → {0,1}, which is defined as follows:
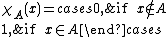
(Here we interpret 1 as true and 0 as false.) The role of the characteristic function is to determine which elements belong or not to a certain subset. Since in any category subobjects are identified as monic arrows
Monomorphism
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
, we identify the value true with the arrow: true: {0} → {0, 1} which maps 0 to 1. Given this definition it can be easily seen that the subset A can be uniquely defined through the characteristic function A = χA−1(1). Therefore the diagram
is a pullback
Pullback (category theory)
In category theory, a branch of mathematics, a pullback is the limit of a diagram consisting of two morphisms f : X → Z and g : Y → Z with a common codomain; it is the limit of the cospan X \rightarrow Z \leftarrow Y...
.
The above example of subobject classifier in Set is very useful because it enables us to easily prove the following axiom:
Axiom: Given a category C, then there exists an isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
,
- y: SubC(X) ≅ HomC(X, Ω) ∀ X ∈ C
In Set this axiom can be restated as follows:
Axiom: The collection of all subsets of S denoted by
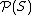, and the collection of all maps from S to the set {0, 1} = 2 denoted by 2S are isomorphic i.e. the function , which in terms of single elements of 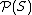is A → χA, is a bijectionBijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
.
The above axiom implies the alternative definition of a subobject classifier:
Definition: Ω is a subobject classifier iff there is a one to one correspondence between subobjects of X and morphisms from X to Ω.
Definition
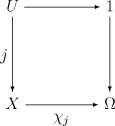
For the general definition, we start with a category C that has a terminal object, which we denote by 1. The object Ω of C is a subobject classifier for C if there exists a morphism- 1 → Ω
with the following property:
- for each monomorphismMonomorphismIn the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
j: U → X there is a unique morphism χ j: X → Ω such that the following commutative diagramCommutative diagramIn mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
- is a pullback diagram — that is, U is the limitLimit (category theory)In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products and inverse limits....
of the diagram:
The morphism χ j is then called the classifying morphism for the subobject represented by j.
Further examples
Every toposTopos
In mathematics, a topos is a type of category that behaves like the category of sheaves of sets on a topological space...
has a subobject classifier. For the topos of sheaves
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
of sets on a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X, it can be described in these terms: For any open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
U of X,
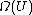is the set of all open subsets of U. Roughly speaking an assertion inside this topos is variably true or false, and its truth value from the viewpoint of an open subset U is the open subset of U where the assertion is true.For a small category
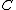, the subobject classifer in the topos of presheaves is given as follows. For any , 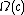is the set of sievesSieve (category theory)
In category theory, a branch of mathematics, a sieve is a way of choosing arrows with a common codomain. It is a categorical analogue of a collection of open subsets of a fixed open set in topology. In a Grothendieck topology, certain sieves become categorical analogues of open covers in...
on
.