Étale topology
Encyclopedia
In algebraic geometry
, the étale topology is a Grothendieck topology
on the category of scheme
s which has properties similar to the Euclidean topology, but unlike the Euclidean topology, it is also defined in positive characteristic. The étale topology was originally introduced by Grothendieck to define étale cohomology
, and this is still the étale topology's most well-known use.
s from a scheme to X. This is the analog of the category of open subsets of X (that is, the category whose objects are varieties and whose morphisms are open immersions). Its objects can be informally thought of as étale open subsets of X. The intersection of two objects corresponds to their fibered product over X. Ét(X) is a large category, meaning that its objects do not form a set.
An étale presheaf on X is a contravariant functor from Ét(X) to the category of sets. A presheaf F is called an étale sheaf if it satisfies the analog of the usual gluing condition for sheaves on topological spaces. That is, F is an étale sheaf if and only if the following condition is true. Suppose that is an object of Ét(X) and that is a jointly surjective family of étale morphisms over X. For each i, choose a section xi of F over Ui. The projection map , which is loosely speaking the inclusion of the intersection of Ui and Uj in Ui, induces a restriction map . If for all i and j the restrictions of xi and xj to are equal, then there must exist a unique section x of F over U which restricts to xi for all i.
Suppose that X is a Noetherian scheme. An abelian étale sheaf F on X is called finite locally constant if it is a representable functor which can be represented by an étale cover of X. It is called constructible if X can be covered by a finite family of subschemes on each of which the restriction of F is finite locally constant. It is called torsion if F(U) is a torsion group for all étale covers U of X. Finite locally constant sheaves are constructible, and constructible sheaves are torsion. Every torsion sheaf is a filtered inductive limit of constructible sheaves.
Grothendieck originally introduced the machinery of Grothendieck topologies and topoi
to define the étale topology. In this language, the definition of the étale topology is succinct but abstract: It is the topology generated by the pretopology whose covering families are jointly surjective families of étale morphisms. The small étale site of X is the category O(Xét) whose objects are schemes U with a fixed étale morphism U → X. The morphisms are morphisms of schemes compatible with the fixed maps to X. The big étale site of X is the category Ét/X, that is, the category of schemes with a fixed map to X, considered with the étale topology.
The étale topology can be defined using slightly less data. First, notice that the étale topology is finer than the Zariski topology. Consequently, to define an étale cover of a scheme X, it suffices to first cover X by open affine subschemes, that is, to take a Zariski cover, and then to define an étale cover of an affine scheme. An étale cover of an affine scheme X can be defined as a surjective family {uα : Xα → X} such that the set of all α is finite, each Xα is affine, and each uα is étale. Then an étale cover of X is a family {uα : Xα → X} which becomes an étale cover after base changing to any open affine subscheme of X.
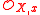. It is usually denoted 
.
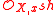Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, the étale topology is a Grothendieck topology
Grothendieck topology
In category theory, a branch of mathematics, a Grothendieck topology is a structure on a category C which makes the objects of C act like the open sets of a topological space. A category together with a choice of Grothendieck topology is called a site.Grothendieck topologies axiomatize the notion...
on the category of scheme
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
s which has properties similar to the Euclidean topology, but unlike the Euclidean topology, it is also defined in positive characteristic. The étale topology was originally introduced by Grothendieck to define étale cohomology
Étale cohomology
In mathematics, the étale cohomology groups of an algebraic variety or scheme are algebraic analogues of the usual cohomology groups with finite coefficients of a topological space, introduced by Grothendieck in order to prove the Weil conjectures...
, and this is still the étale topology's most well-known use.
Definitions
For any scheme X, let Ét(X) be the category of all étale morphismÉtale morphism
In algebraic geometry, a field of mathematics, an étale morphism is an algebraic analogue of the notion of a local isomorphism in the complex analytic topology. They satisfy the hypotheses of the implicit function theorem, but because open sets in the Zariski topology are so large, they are not...
s from a scheme to X. This is the analog of the category of open subsets of X (that is, the category whose objects are varieties and whose morphisms are open immersions). Its objects can be informally thought of as étale open subsets of X. The intersection of two objects corresponds to their fibered product over X. Ét(X) is a large category, meaning that its objects do not form a set.
An étale presheaf on X is a contravariant functor from Ét(X) to the category of sets. A presheaf F is called an étale sheaf if it satisfies the analog of the usual gluing condition for sheaves on topological spaces. That is, F is an étale sheaf if and only if the following condition is true. Suppose that is an object of Ét(X) and that is a jointly surjective family of étale morphisms over X. For each i, choose a section xi of F over Ui. The projection map , which is loosely speaking the inclusion of the intersection of Ui and Uj in Ui, induces a restriction map . If for all i and j the restrictions of xi and xj to are equal, then there must exist a unique section x of F over U which restricts to xi for all i.
Suppose that X is a Noetherian scheme. An abelian étale sheaf F on X is called finite locally constant if it is a representable functor which can be represented by an étale cover of X. It is called constructible if X can be covered by a finite family of subschemes on each of which the restriction of F is finite locally constant. It is called torsion if F(U) is a torsion group for all étale covers U of X. Finite locally constant sheaves are constructible, and constructible sheaves are torsion. Every torsion sheaf is a filtered inductive limit of constructible sheaves.
Grothendieck originally introduced the machinery of Grothendieck topologies and topoi
Topos
In mathematics, a topos is a type of category that behaves like the category of sheaves of sets on a topological space...
to define the étale topology. In this language, the definition of the étale topology is succinct but abstract: It is the topology generated by the pretopology whose covering families are jointly surjective families of étale morphisms. The small étale site of X is the category O(Xét) whose objects are schemes U with a fixed étale morphism U → X. The morphisms are morphisms of schemes compatible with the fixed maps to X. The big étale site of X is the category Ét/X, that is, the category of schemes with a fixed map to X, considered with the étale topology.
The étale topology can be defined using slightly less data. First, notice that the étale topology is finer than the Zariski topology. Consequently, to define an étale cover of a scheme X, it suffices to first cover X by open affine subschemes, that is, to take a Zariski cover, and then to define an étale cover of an affine scheme. An étale cover of an affine scheme X can be defined as a surjective family {uα : Xα → X} such that the set of all α is finite, each Xα is affine, and each uα is étale. Then an étale cover of X is a family {uα : Xα → X} which becomes an étale cover after base changing to any open affine subscheme of X.
Local rings in the étale topology
Let X be a scheme with its étale topology, and fix a point x of X. In the Zariski topology, the stalk of X at x is computed by taking a direct limit of the sections of the structure sheaf over all the Zariski open neighborhoods of x. In the étale topology, there are strictly more open neighborhoods of x, so the correct analog of the local ring at x is formed by taking the limit over a strictly larger family. The correct analog of the local ring at x for the étale topology turns out to be the strict henselization of the local ring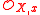. It is usually denoted .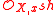