.gif)
Range (mathematics)
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the range of a function
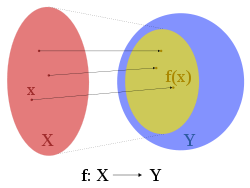
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
refers to either the codomain
Codomain
In mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...
or the image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of the function, depending upon usage. This ambiguity is illustrated by the function
 that maps real numbers to real numbers with
that maps real numbers to real numbers with 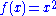 . Some books say that range of this function is its codomain, the set of all real number
. Some books say that range of this function is its codomain, the set of all real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, reflecting that the function is real-valued. These books call the actual output of the function the image. This is the current usage for range in computer science
Range (computer science)
In computer science, the term range may refer to one of three things:# The possible values that may be stored in a variable.# The upper and lower bounds of an array.# An alternative to iterator.-Range of a variable:...
. Other books say that the range is the function's image, the set of non-negative real numbers, reflecting that a number can be the output of this function if and only if it is a non-negative real number. In this case, the larger set containing the range is called the codomain. This usage is more common in modern mathematics.
Because of this ambiguity, it is a good idea to specify whether it is the image or the codomain being discussed.
Examples
Let f be a function on the real numbers defined by
defined by 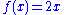 . This function takes as input any real number and outputs a real number two times the input. In this case, the codomain and the image are the same (i.e., the function is a surjection
. This function takes as input any real number and outputs a real number two times the input. In this case, the codomain and the image are the same (i.e., the function is a surjectionSurjective function
In mathematics, a function f from a set X to a set Y is surjective , or a surjection, if every element y in Y has a corresponding element x in X so that f = y...
), so the range is unambiguous; it is the set of all real numbers.
In contrast, consider the function
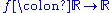 defined by
defined by 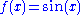 . If the word "range" is used in the first sense given above, we would say the range of f is the codomain, all real numbers; but since the output of the sine
. If the word "range" is used in the first sense given above, we would say the range of f is the codomain, all real numbers; but since the output of the sineSine
In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
function is always between -1 and 1, "range" in the second sense would say the range is the image, the closed interval from -1 to 1.
Formal definition
Standard mathematical notation allows a formal definition of range.In the first sense, the range of a function must be specified; it is often assumed to be the set of all real numbers, and {y | there exists an x in the domain of f such that y = f(x)} is called the image of f.
In the second sense, the range of a function f is {y | there exists an x in the domain of f such that y = f(x)}. In this case, the codomain of f must be specified, but is often assumed to be the set of all real numbers.
In both cases, image f ⊆ range f ⊆ codomain f, with at least one of the containments being equality.

