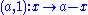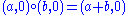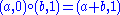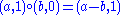Symmetry groups in one dimension
Encyclopedia
A one-dimensional symmetry group is a mathematical group
that describes symmetries
in one dimension (1D).
A pattern in 1D can be represented as a function f(x) for, say, the color at position x.
The 1D isometries
map x to x + a and to a − x. Isometries which leave the function unchanged are translation
s x + a with a such that f(x + a) = f(x) and reflection
s a − x with a such that f(a − x) = f(x).
, i.e., functions f(x) such that for some a > 0, f(x + a) = f(x) for all x. For these patterns, the values of a for which this property holds form a group
.
, i.e., for which the positive values in the group have a minimum. By rescaling we make this minimum value 1.
Such patterns fall in two categories, the two 1D space group
s or line group
s.
In the simpler case the only isometries of R which map the pattern to itself are translations; this applies, e.g., for the pattern
− −−− − −−− − −−− − −−−
Each isometry can be characterized by an integer, namely plus or minus the translation distance. Therefore the symmetry group
is Z.
In the other case, among the isometries of R which map the pattern to itself there are also reflections; this applies, e.g., for the pattern
− −−− − − −−− − − −−− −
We choose the origin for x at one of the points of reflection. Now all reflections which map the pattern to itself are of the form a−x where the constant "a" is an integer (the increments of a are 1 again, because we can combine a reflection and a translation to get another reflection, and we can combine two reflections to get a translation). Therefore all isometries can be characterized by an integer and a code, say 0 or 1, for translation or reflection.
Thus:
The latter is a reflection with respect to the point a/2 (an integer or an integer plus 1/2).
Group operations (function composition
, the one on the right first) are, for integers a and b:
E.g., in the third case: translation by an amount b changes x into x + b, reflection with respect to 0 gives−x − b, and a translation a gives a − b − x.
This group is called the generalized dihedral group of Z, Dih(Z), and also D∞. It is a semidirect product
of Z and C2. It has a normal subgroup
of index
2 isomorphic to Z: the translations. Also it contains an element f of order 2 such that, for all n in Z, n f = f n −1: the reflection with respect to the reference point, (0,1).
The two groups are called lattice groups
. The lattice
is Z. As translation cell we can take the interval 0 ≤ x < 1. In the first case the fundamental domain
can be taken the same; topologically it is a circle (1-torus
); in the second case we can take 0 ≤ x ≤ 0.5.
The actual discrete symmetry group of a translationally symmetric pattern can be:
The set of translationally symmetric patterns can thus be classified by actual symmetry group, while actual symmetry groups, in turn, can be classified as type 1 or type 2.
These space group types are the symmetry groups “up to conjugacy with respect to affine transformations”: the affine transformation changes the translation distance to the standard one (above: 1), and the position of one of the points of reflections, if applicable, to the origin. Thus the actual symmetry group contains elements of the form gag−1= b, which is a conjugate of a.
There are also less trivial patterns/functions with translational symmetry for arbitrarily small translations, e.g. the group of translations by rational distances. Even apart from scaling and shifting, there are infinitely many cases, e.g. by considering rational numbers of which the denominators are powers of a given prime number.
The translations form a group of isometries. However, there is no pattern with this group as symmetry group.
s):
, i.e. grey is not between black and white, the three colors are simply all different.
Even with nominal colors there can be a special kind of symmetry, as in:
−−−−−−− -- − −−− − − −
(reflection gives the negative image). This is also not included in the classification.
s of the symmetry group that can be considered in this connection are:
This section illustrates group action concepts for these cases.
The action of G on X is called
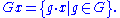
Case that the group action is on R:
Case that the group action is on patterns:
The set of all orbits of X under the action of G is written as X/G.
If Y is a subset
of X, we write GY for the set {g · y : y
Y and g 
G}. We call the subset Y invariant under G if GY = Y (which is equivalent to GY ⊆ Y). In that case, G also operates on Y. The subset Y is called fixed under G if g · y = yfor all g in G and all y in Y. In the example of the orbit {−8,−6,2,4,12,14,22,24,..}, {−9,−8,−6,−5,1,2,4,5,11,12,14,15,21,22,24,25,..} is invariant under G, but not fixed.
For every x in X, we define the stabilizer subgroup of x (also called the isotropy group orlittle group) as the set of all elements in G that fix x: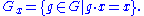
If x is a reflection point, its stabilizer is the group of order two containing the identity and the reflection inx. In other cases the stabilizer is the trivial group.
For a fixed x in X, consider the map from G to X given by g |-> g · x. The image
of this map is the orbit of x and the coimage
is the set of all left coset
s ofGx. The standard quotient theorem of set theory then gives a natural bijection
betweenG/Gx and Gx. Specifically, the bijection is given by hGx |-> h · x. This result is known as the orbit-stabilizer theorem. If, in the example, we take x = 3, the orbit is {−7,3,13,23,..}, and the two groups are isomorphic with Z.
If two elements x and y belong to the same orbit, then their stabilizer subgroups, Gx andGy, are isomorphic
. More precisely: if y = g · x, thenGy = gGx g−1. In the example this applies e.g. for 3 and 23, both reflection points. Reflection about 23 corresponds to a translation of −20, reflection about 3, and translation of 20.
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
that describes symmetries
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
in one dimension (1D).
A pattern in 1D can be represented as a function f(x) for, say, the color at position x.
The 1D isometries
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
map x to x + a and to a − x. Isometries which leave the function unchanged are translation
Translation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
s x + a with a such that f(x + a) = f(x) and reflection
Reflection (mathematics)
In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
s a − x with a such that f(a − x) = f(x).
Translational symmetry
Consider all patterns in 1D which have translational symmetrySymmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
, i.e., functions f(x) such that for some a > 0, f(x + a) = f(x) for all x. For these patterns, the values of a for which this property holds form a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
.
Discrete symmetry groups
We first consider patterns for which the group is discreteDiscrete group
In mathematics, a discrete group is a group G equipped with the discrete topology. With this topology G becomes a topological group. A discrete subgroup of a topological group G is a subgroup H whose relative topology is the discrete one...
, i.e., for which the positive values in the group have a minimum. By rescaling we make this minimum value 1.
Such patterns fall in two categories, the two 1D space group
Space group
In mathematics and geometry, a space group is a symmetry group, usually for three dimensions, that divides space into discrete repeatable domains.In three dimensions, there are 219 unique types, or counted as 230 if chiral copies are considered distinct...
s or line group
Line group
A line group is a mathematical way of describing symmetries associated with moving along a line. These symmetries include repeating along that line, making that line a one-dimensional lattice...
s.
In the simpler case the only isometries of R which map the pattern to itself are translations; this applies, e.g., for the pattern
− −−− − −−− − −−− − −−−
Each isometry can be characterized by an integer, namely plus or minus the translation distance. Therefore the symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
is Z.
In the other case, among the isometries of R which map the pattern to itself there are also reflections; this applies, e.g., for the pattern
− −−− − − −−− − − −−− −
We choose the origin for x at one of the points of reflection. Now all reflections which map the pattern to itself are of the form a−x where the constant "a" is an integer (the increments of a are 1 again, because we can combine a reflection and a translation to get another reflection, and we can combine two reflections to get a translation). Therefore all isometries can be characterized by an integer and a code, say 0 or 1, for translation or reflection.
Thus:
The latter is a reflection with respect to the point a/2 (an integer or an integer plus 1/2).
Group operations (function composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
, the one on the right first) are, for integers a and b:
E.g., in the third case: translation by an amount b changes x into x + b, reflection with respect to 0 gives−x − b, and a translation a gives a − b − x.
This group is called the generalized dihedral group of Z, Dih(Z), and also D∞. It is a semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
of Z and C2. It has a normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of index
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
2 isomorphic to Z: the translations. Also it contains an element f of order 2 such that, for all n in Z, n f = f n −1: the reflection with respect to the reference point, (0,1).
The two groups are called lattice groups
Lattice (group)
In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
. The lattice
Lattice (group)
In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
is Z. As translation cell we can take the interval 0 ≤ x < 1. In the first case the fundamental domain
Fundamental domain
In geometry, the fundamental domain of a symmetry group of an object is a part or pattern, as small or irredundant as possible, which determines the whole object based on the symmetry. More rigorously, given a topological space and a group acting on it, the images of a single point under the group...
can be taken the same; topologically it is a circle (1-torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
); in the second case we can take 0 ≤ x ≤ 0.5.
The actual discrete symmetry group of a translationally symmetric pattern can be:
- of group 1 type, for any positive value of the smallest translation distance
- of group 2 type, for any positive value of the smallest translation distance, and any positioning of the lattice of points of reflection (which is twice as dense as the translation lattice)
The set of translationally symmetric patterns can thus be classified by actual symmetry group, while actual symmetry groups, in turn, can be classified as type 1 or type 2.
These space group types are the symmetry groups “up to conjugacy with respect to affine transformations”: the affine transformation changes the translation distance to the standard one (above: 1), and the position of one of the points of reflections, if applicable, to the origin. Thus the actual symmetry group contains elements of the form gag−1= b, which is a conjugate of a.
Non-discrete symmetry groups
For a homogeneous “pattern” the symmetry group contains all translations, and reflection in all points. The symmetry group is isomorphic to Dih(R).There are also less trivial patterns/functions with translational symmetry for arbitrarily small translations, e.g. the group of translations by rational distances. Even apart from scaling and shifting, there are infinitely many cases, e.g. by considering rational numbers of which the denominators are powers of a given prime number.
The translations form a group of isometries. However, there is no pattern with this group as symmetry group.
Patterns without translational symmetry
For a pattern without translational symmetry there are the following possibilities (1D point groupPoint group
In geometry, a point group is a group of geometric symmetries that keep at least one point fixed. Point groups can exist in a Euclidean space with any dimension, and every point group in dimension d is a subgroup of the orthogonal group O...
s):
- the symmetry group is the trivial group (no symmetry)
- the symmetry group is one of the groups each consisting of the identity and reflection in a point (isomorphic toC2)
1D-symmetry of a function vs. 2D-symmetry of its graph
Symmetries of a function (in the sense of this article) imply corresponding symmetries of its graph. However, 2-fold rotational symmetry of the graph does not imply any symmetry (in the sense of this article) of the function: function values (in a pattern representing colors, grey shades, etc.) are nominal dataLevel of measurement
The "levels of measurement", or scales of measure are expressions that typically refer to the theory of scale types developed by the psychologist Stanley Smith Stevens. Stevens proposed his theory in a 1946 Science article titled "On the theory of scales of measurement"...
, i.e. grey is not between black and white, the three colors are simply all different.
Even with nominal colors there can be a special kind of symmetry, as in:
−−−−−−− -- − −−− − − −
(reflection gives the negative image). This is also not included in the classification.
Group action
Group actionGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
s of the symmetry group that can be considered in this connection are:
- on R
- on the set of real functions of a real variable (each representing a pattern)
This section illustrates group action concepts for these cases.
The action of G on X is called
- transitive if for any two x, y in X there exists a g in G such that g · x = y; for neither of the two group actions this is the case for any discrete symmetry group
- faithful (or effective) if for any two different g, h in G there exists an x in X such thatg · x ≠ h · x; for both group actions this is the case for any discrete symmetry group (because, except for the identity, symmetry groups do not contain elements that “do nothing”)
- free if for any two different g , h in G and all x in X we have g · x ≠ h · x; this is the case if there are no reflections
- regular (or simply transitive) if it is both transitive and free; this is equivalent to saying that for any twox, y in X there exists precisely one g in G such that g · x = y.
Orbits and stabilizers
Consider a group G acting on a set X. The orbit of a point x in X is the set of elements of X to which x can be moved by the elements of G. The orbit of x is denoted by Gx: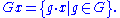Case that the group action is on R:
- For the trivial group, all orbits contain only one element; for a group of translations, an orbit is e.g. {..,−9,1,11,21,..}, for a reflection e.g. {2,4}, and for the symmetry group with translations and reflections, e.g., {−8,−6,2,4,12,14,22,24,..} (translation distance is 10, points of reflection are ..,−7,−2,3,8,13,18,23,..). The points within an orbit are “equivalent”. If a symmetry group applies for a pattern, then within each orbit the color is the same.
Case that the group action is on patterns:
- The orbits are sets of patterns, containing translated and/or reflected versions, “equivalent patterns”. A translation of a pattern is only equivalent if the translation distance is one of those included in the symmetry group considered, and similarly for a mirror image.
The set of all orbits of X under the action of G is written as X/G.
If Y is a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of X, we write GY for the set {g · y : y
Y and g G}. We call the subset Y invariant under G if GY = Y (which is equivalent to GY ⊆ Y). In that case, G also operates on Y. The subset Y is called fixed under G if g · y = yfor all g in G and all y in Y. In the example of the orbit {−8,−6,2,4,12,14,22,24,..}, {−9,−8,−6,−5,1,2,4,5,11,12,14,15,21,22,24,25,..} is invariant under G, but not fixed.For every x in X, we define the stabilizer subgroup of x (also called the isotropy group orlittle group) as the set of all elements in G that fix x:
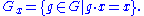
If x is a reflection point, its stabilizer is the group of order two containing the identity and the reflection inx. In other cases the stabilizer is the trivial group.
For a fixed x in X, consider the map from G to X given by g |-> g · x. The image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of this map is the orbit of x and the coimage
Coimage
In algebra, the coimage of a homomorphismis the quotientof domain and kernel.The coimage is canonically isomorphic to the image by the first isomorphism theorem, when that theorem applies....
is the set of all left coset
Coset
In mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
s ofGx. The standard quotient theorem of set theory then gives a natural bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
betweenG/Gx and Gx. Specifically, the bijection is given by hGx |-> h · x. This result is known as the orbit-stabilizer theorem. If, in the example, we take x = 3, the orbit is {−7,3,13,23,..}, and the two groups are isomorphic with Z.
If two elements x and y belong to the same orbit, then their stabilizer subgroups, Gx andGy, are isomorphic
Group isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
. More precisely: if y = g · x, thenGy = gGx g−1. In the example this applies e.g. for 3 and 23, both reflection points. Reflection about 23 corresponds to a translation of −20, reflection about 3, and translation of 20.
See also
- Line groupLine groupA line group is a mathematical way of describing symmetries associated with moving along a line. These symmetries include repeating along that line, making that line a one-dimensional lattice...
- Frieze groupFrieze groupA frieze group is a mathematical concept to classify designs on two-dimensional surfaces which are repetitive in one direction, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art...
- Space groupSpace groupIn mathematics and geometry, a space group is a symmetry group, usually for three dimensions, that divides space into discrete repeatable domains.In three dimensions, there are 219 unique types, or counted as 230 if chiral copies are considered distinct...
- Wallpaper groupWallpaper groupA wallpaper group is a mathematical classification of a two-dimensional repetitive pattern, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art...