
Chirality (mathematics)
Encyclopedia
In geometry
, a figure is chiral (and said to have chirality) if it is not identical to its mirror image
, or, more precisely, if it cannot be mapped to its mirror image by rotation
s and translation
s alone. For example, a right shoe is different from a left shoe, and clockwise is different from counterclockwise.
A chiral object and its mirror image are said to be enantiomorphs. The word chirality is derived from the Greek (cheir), the hand, the most familiar chiral object; the word enantiomorph stems from the Greek (enantios) 'opposite' + (morphe) 'form'. A non-chiral figure is called achiral or amphichiral.
The helix
(and by extension a spun string, a screw, a propeller, etc.) and Möbius strip
are chiral two-dimensional objects in three-dimensional ambient space. The J, L, S and Z-shaped tetromino
es of the popular video game Tetris
also exhibit chirality, but only in a two-dimensional space.
Many other familiar objects exhibit the same chiral symmetry of the human body, such as gloves, glasses (for two lenses of different prescription), and shoes. A similar notion of chirality is considered in knot theory
, as explained below.
Some chiral three-dimensional objects, such as the helix, can be assigned a right or left handedness, according to the right-hand rule
.
contains at least one orientation-reversing isometry. (In Euclidean geometry any isometry
can be written as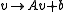 with an orthogonal matrix
with an orthogonal matrix
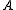 and a vector
and a vector 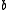 . The determinant
. The determinant
of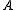 is either 1 or −1 then. If it is −1 the isometry is orientation
is either 1 or −1 then. If it is −1 the isometry is orientation
-reversing, otherwise it is orientation-preserving.)
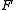 is a plane
is a plane 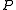 , such that
, such that  is invariant under the mapping
is invariant under the mapping 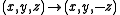 , when
, when 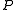 is chosen to be the
is chosen to be the  -
-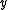 -plane of the coordinate system. A center of symmetry of a figure
-plane of the coordinate system. A center of symmetry of a figure 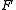 is a point
is a point 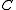 , such that
, such that 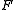 is invariant under the mapping
is invariant under the mapping 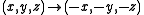 , when
, when 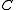 is chosen to be the origin of the coordinate system.) Note, however, that there are achiral figures lacking both plane and center of symmetry. An example is the figure
is chosen to be the origin of the coordinate system.) Note, however, that there are achiral figures lacking both plane and center of symmetry. An example is the figure
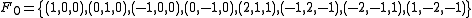
which is invariant under the orientation reversing isometry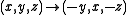 and thus achiral, but it has neither plane nor center of symmetry. The figure
and thus achiral, but it has neither plane nor center of symmetry. The figure

also is achiral as the origin is a center of symmetry, but it lacks a plane of symmetry.
Note also that achiral figures can have a center axis.
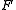 is a line
is a line 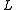 , such that
, such that  is invariant under the mapping
is invariant under the mapping 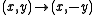 , when
, when 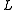 is chosen to be the
is chosen to be the  -axis of the coordinate system.) Consider the following pattern:
-axis of the coordinate system.) Consider the following pattern:
> > > > > > > > > >
> > > > > > > > > >
This figure is chiral, as it is not identical to its mirror image from either axis:
> > > > > > > > > > or < < < < < < < < < <
> > > > > > > > > > < < < < < < < < < <
But if one prolongs the pattern in both directions to infinity, one receives an (unbounded) achiral figure which has no axis of symmetry. Its symmetry group is a frieze group
generated by a single glide reflection
.
is called achiral
if it can be continuously deformed into its mirror image, otherwise it is called chiral. For example the unknot
and the figure-eight knot
are achiral, whereas the trefoil knot
is chiral.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a figure is chiral (and said to have chirality) if it is not identical to its mirror image
Mirror image
A mirror image is a reflected duplication of an object that appears identical but reversed. As an optical effect it results from reflection off of substances such as a mirror or water. It is also a concept in geometry and can be used as a conceptualization process for 3-D structures...
, or, more precisely, if it cannot be mapped to its mirror image by rotation
Rotation (mathematics)
In geometry and linear algebra, a rotation is a transformation in a plane or in space that describes the motion of a rigid body around a fixed point. A rotation is different from a translation, which has no fixed points, and from a reflection, which "flips" the bodies it is transforming...
s and translation
Translation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
s alone. For example, a right shoe is different from a left shoe, and clockwise is different from counterclockwise.
A chiral object and its mirror image are said to be enantiomorphs. The word chirality is derived from the Greek (cheir), the hand, the most familiar chiral object; the word enantiomorph stems from the Greek (enantios) 'opposite' + (morphe) 'form'. A non-chiral figure is called achiral or amphichiral.
The helix
Helix
A helix is a type of smooth space curve, i.e. a curve in three-dimensional space. It has the property that the tangent line at any point makes a constant angle with a fixed line called the axis. Examples of helixes are coil springs and the handrails of spiral staircases. A "filled-in" helix – for...
(and by extension a spun string, a screw, a propeller, etc.) and Möbius strip
Möbius strip
The Möbius strip or Möbius band is a surface with only one side and only one boundary component. The Möbius strip has the mathematical property of being non-orientable. It can be realized as a ruled surface...
are chiral two-dimensional objects in three-dimensional ambient space. The J, L, S and Z-shaped tetromino
Tetromino
A tetromino is a geometric shape composed of four squares, connected orthogonally. This, like dominoes and pentominoes, is a particular type of polyomino...
es of the popular video game Tetris
Tetris
Tetris is a puzzle video game originally designed and programmed by Alexey Pajitnov in the Soviet Union. It was released on June 6, 1984, while he was working for the Dorodnicyn Computing Centre of the Academy of Science of the USSR in Moscow, Russian Soviet Federative Socialist Republic...
also exhibit chirality, but only in a two-dimensional space.
Many other familiar objects exhibit the same chiral symmetry of the human body, such as gloves, glasses (for two lenses of different prescription), and shoes. A similar notion of chirality is considered in knot theory
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
, as explained below.
Some chiral three-dimensional objects, such as the helix, can be assigned a right or left handedness, according to the right-hand rule
Right-hand rule
In mathematics and physics, the right-hand rule is a common mnemonic for understanding notation conventions for vectors in 3 dimensions. It was invented for use in electromagnetism by British physicist John Ambrose Fleming in the late 19th century....
.
Chirality and symmetry group
A figure is achiral if and only if its symmetry groupSymmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
contains at least one orientation-reversing isometry. (In Euclidean geometry any isometry
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
can be written as
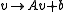 with an orthogonal matrix
with an orthogonal matrixOrthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
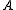 and a vector
and a vector 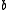 . The determinant
. The determinantDeterminant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of
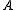 is either 1 or −1 then. If it is −1 the isometry is orientation
is either 1 or −1 then. If it is −1 the isometry is orientationOrientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
-reversing, otherwise it is orientation-preserving.)
Chirality in three dimensions
In three dimensions, every figure which possesses a plane of symmetry or a center of symmetry is achiral. (A plane of symmetry of a figure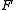 is a plane
is a plane 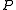 , such that
, such that  is invariant under the mapping
is invariant under the mapping 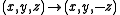 , when
, when 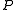 is chosen to be the
is chosen to be the  -
-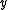 -plane of the coordinate system. A center of symmetry of a figure
-plane of the coordinate system. A center of symmetry of a figure 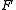 is a point
is a point 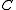 , such that
, such that 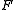 is invariant under the mapping
is invariant under the mapping 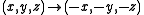 , when
, when  is chosen to be the origin of the coordinate system.) Note, however, that there are achiral figures lacking both plane and center of symmetry. An example is the figure
is chosen to be the origin of the coordinate system.) Note, however, that there are achiral figures lacking both plane and center of symmetry. An example is the figure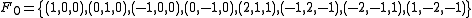
which is invariant under the orientation reversing isometry
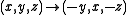 and thus achiral, but it has neither plane nor center of symmetry. The figure
and thus achiral, but it has neither plane nor center of symmetry. The figure
also is achiral as the origin is a center of symmetry, but it lacks a plane of symmetry.
Note also that achiral figures can have a center axis.
Chirality in two dimensions
In two dimensions, every figure which possesses an axis of symmetry is achiral, and it can be shown that every bounded achiral figure must have an axis of symmetry. (An axis of symmetry of a figure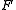 is a line
is a line 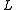 , such that
, such that  is invariant under the mapping
is invariant under the mapping 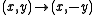 , when
, when 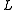 is chosen to be the
is chosen to be the  -axis of the coordinate system.) Consider the following pattern:
-axis of the coordinate system.) Consider the following pattern:> > > > > > > > > >
> > > > > > > > > >
This figure is chiral, as it is not identical to its mirror image from either axis:
> > > > > > > > > > or < < < < < < < < < <
> > > > > > > > > > < < < < < < < < < <
But if one prolongs the pattern in both directions to infinity, one receives an (unbounded) achiral figure which has no axis of symmetry. Its symmetry group is a frieze group
Frieze group
A frieze group is a mathematical concept to classify designs on two-dimensional surfaces which are repetitive in one direction, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art...
generated by a single glide reflection
Glide reflection
In geometry, a glide reflection is a type of isometry of the Euclidean plane: the combination of a reflection in a line and a translation along that line. Reversing the order of combining gives the same result...
.
Knot theory
A knotKnot (mathematics)
In mathematics, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3, considered up to continuous deformations . A crucial difference between the standard mathematical and conventional notions of a knot is that mathematical knots are closed—there are no ends to tie or untie on a...
is called achiral
Amphichiral knot
In the mathematical field of knot theory, a chiral knot is a knot that is not equivalent to its mirror image. An oriented knot that is equivalent to its mirror image is an amphichiral knot, also called an achiral knot or amphicheiral knot. The chirality of a knot is a knot invariant...
if it can be continuously deformed into its mirror image, otherwise it is called chiral. For example the unknot
Unknot
The unknot arises in the mathematical theory of knots. Intuitively, the unknot is a closed loop of rope without a knot in it. A knot theorist would describe the unknot as an image of any embedding that can be deformed, i.e. ambient-isotoped, to the standard unknot, i.e. the embedding of the...
and the figure-eight knot
Figure-eight knot (mathematics)
In knot theory, a figure-eight knot is the unique knot with a crossing number of four. This is the smallest possible crossing number except for the unknot and trefoil knot...
are achiral, whereas the trefoil knot
Trefoil knot
In topology, a branch of mathematics, the trefoil knot is the simplest example of a nontrivial knot. The trefoil can be obtained by joining together the two loose ends of a common overhand knot, resulting in a knotted loop...
is chiral.
See also
- Chirality (physics)Chirality (physics)A chiral phenomenon is one that is not identical to its mirror image . The spin of a particle may be used to define a handedness for that particle. A symmetry transformation between the two is called parity...
- Chirality (chemistry)Chirality (chemistry)A chiral molecule is a type of molecule that lacks an internal plane of symmetry and thus has a non-superimposable mirror image. The feature that is most often the cause of chirality in molecules is the presence of an asymmetric carbon atom....
- Orientation (mathematics)Orientation (mathematics)In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
- Right-hand ruleRight-hand ruleIn mathematics and physics, the right-hand rule is a common mnemonic for understanding notation conventions for vectors in 3 dimensions. It was invented for use in electromagnetism by British physicist John Ambrose Fleming in the late 19th century....
- HandednessHandednessHandedness is a human attribute defined by unequal distribution of fine motor skills between the left and right hands. An individual who is more dexterous with the right hand is called right-handed and one who is more skilled with the left is said to be left-handed...
- AsymmetryAsymmetryAsymmetry is the absence of, or a violation of, symmetry.-In organisms:Due to how cells divide in organisms, asymmetry in organisms is fairly usual in at least one dimension, with biological symmetry also being common in at least one dimension....
- SkewnessSkewnessIn probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable. The skewness value can be positive or negative, or even undefined...
- Vertex algebra
External links
- The Mathematical Theory of Chirality by Michel Petitjean
- Symmetry, Chirality, Symmetry Measures and Chirality Measures: General Definitions
- Petitjean, Michel (2010). Chirality in Metric Spaces, Symmetry: Culture and Science 21(1-3), pp. 27-36
- Chiral Polyhedra by Eric W. WeissteinEric W. WeissteinEric W. Weisstein is an encyclopedist who created and maintains MathWorld and Eric Weisstein's World of Science . He currently works for Wolfram Research, Inc.-Education:...
, The Wolfram Demonstrations Project. - When Topology Meets Chemistry by Erica Flapan.

