
Snub (geometry)
Encyclopedia
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
or tiling
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
that removes alternate vertices. Only even-sided polyhedra can be alternated, for example the zonohedra
Zonohedron
A zonohedron is a convex polyhedron where every face is a polygon with point symmetry or, equivalently, symmetry under rotations through 180°. Any zonohedron may equivalently be described as the Minkowski sum of a set of line segments in three-dimensional space, or as the three-dimensional...
. Every 2n-sided face becomes n-sided. Square faces disappear into new edges.
An alternation of a regular polyhedron or tiling is sometimes labeled by the regular form, prefixed by an h, standing for half. For example h{4,3} is an alternated cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
(creating a tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
), and h{4,4} is an alternated square tiling (still a square tiling).
Snub
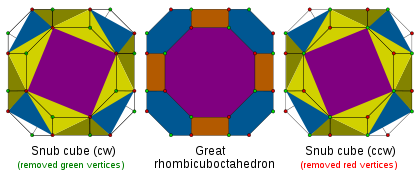
A snub is a related operation. It is an alternation applied to an omnitruncated regular polyhedron. An omnitruncated regular polyhedron or tiling always has even-sided faces and so can always be alternated.For instance the snub cube is created in two steps. First it is omnitruncated, creating the great rhombicuboctahedron. Secondly that polyhedron is alternated into a snub cube. You can see from the picture on the right that there are two ways to alternate the vertices, and they are mirror images of each other, creating two chiral
Chirality (mathematics)
In geometry, a figure is chiral if it is not identical to its mirror image, or, more precisely, if it cannot be mapped to its mirror image by rotations and translations alone. For example, a right shoe is different from a left shoe, and clockwise is different from counterclockwise.A chiral object...
forms.
Another example is the uniform antiprisms. A uniform n-gonal antiprism can be constructed as an alternation of a 2n-gonal prism, and the snub of an n-edge hosohedron. In the case of prisms both alternated forms are identical.
Zonohedra
Zonohedron
A zonohedron is a convex polyhedron where every face is a polygon with point symmetry or, equivalently, symmetry under rotations through 180°. Any zonohedron may equivalently be described as the Minkowski sum of a set of line segments in three-dimensional space, or as the three-dimensional...
can also be alternated. For instance, the rhombic triacontahedron
Rhombic triacontahedron
In geometry, the rhombic triacontahedron is a convex polyhedron with 30 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. It is the polyhedral dual of the icosidodecahedron, and it is a zonohedron....
can be snubbed into either an icosahedron
Icosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
or a dodecahedron depending on which vertices are removed.
Platonic solid generators
Three forms: regularPlatonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
→ omnitruncated → snub.
The Coxeter-Dynkin diagram
Coxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
s are given as well. The omnitruncation actives all of the mirrors (ringed). The alternation is shown as rings with holes.
| Symmetry (p q 2) |
|||
|---|---|---|---|
| Tetrahedral (3 3 2) |
 Tetrahedron Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
 truncated octahedron Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron.... |
 icosahedron Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... (snub tetrahedron) |
| Octahedral (4 3 2) |
 Cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
 Truncated cuboctahedron Truncated cuboctahedron In geometry, the truncated cuboctahedron is an Archimedean solid. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices and 72 edges... |
 snub cube Snub cube In geometry, the snub cube, or snub cuboctahedron, is an Archimedean solid.The snub cube has 38 faces, 6 of which are squares and the other 32 are equilateral triangles. It has 60 edges and 24 vertices. It is a chiral polyhedron, that is, it has two distinct forms, which are mirror images of each... |
| Icosahedral (5 3 2) |
 Dodecahedron |
 Truncated icosidodecahedron Truncated icosidodecahedron In geometry, the truncated icosidodecahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces.... |
 snub dodecahedron Snub dodecahedron In geometry, the snub dodecahedron, or snub icosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces.... |
Regular tiling generators
| Symmetry (p q 2) |
|||
|---|---|---|---|
| Square (4 4 2) |
 (4.4.4.4) |
 (4.8.8) Truncated square tiling In geometry, the truncated square tiling is a semiregular tiling of the Euclidean plane. There is one square and two octagons on each vertex. This is the only edge-to-edge tiling by regular convex polygons which contains an octagon... |
 (3.3.4.3.4) |
| Hexagonal (6 3 2) |
 (6.6.6) |
 (3.4.6.4) Great rhombitrihexagonal tiling In geometry, the truncated trihexagonal tiling is a semiregular tiling of the Euclidean plane. There are one square, one hexagon, and one dodecagon on each vertex... |
 3.3.3.3.6 Snub hexagonal tiling In geometry, the Snub hexagonal tiling is a semiregular tiling of the Euclidean plane. There are four triangles and one hexagon on each vertex... |
Uniform prism generators (dihedral symmetry)
Alternate truncations can be applied to prisms. (A square antiprism may be called a snubbed 4-edge hosohedron, as well as an alternated octagonal prism.)Two steps: 2n-gonal prism
Prism (geometry)
In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
s → n-gonal antiprism
Antiprism
In geometry, an n-sided antiprism is a polyhedron composed of two parallel copies of some particular n-sided polygon, connected by an alternating band of triangles...
.
- square prismCubeIn geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
→ digonal antiprismTetrahedronIn geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
(or demicube)-
 →
→ 
-
- hexagonal prismHexagonal prismIn geometry, the hexagonal prism is a prism with hexagonal base. The shape has 8 faces, 18 edges, and 12 vertices.Since it has eight faces, it is an octahedron. However, the term octahedron is primarily used to refer to the regular octahedron, which has eight triangular faces...
→ triangular antiprismOctahedronIn geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
-
 →
→ 
-
- octagonal prismOctagonal prismIn geometry, the octagonal prism is the sixth in an infinite set of prisms, formed by square sides and two regular octagon caps.If faces are all regular, it is a semiregular polyhedron.- Use :...
→ square antiprismSquare antiprismIn geometry, the square antiprism is the second in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps...
-
 →
→ 
-
- decagonal prismDecagonal prismIn geometry, the decagonal prism is the eighth in an infinite set of prisms, formed by ten square side faces and two regular decagon caps. With twelve faces, it is one of many nonregular dodecahedra.If faces are all regular, it is a semiregular polyhedron....
→ pentagonal antiprismPentagonal antiprismIn geometry, the pentagonal antiprism is the third in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps. It consists of two pentagons joined to each other by a ring of 10 triangles for a total of 12 faces...
-
 →
→ 
-
- ....
Alternate truncations
A similar operation can truncateTruncation (geometry)
In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :...
alternate vertices, rather than just removing them. Below is a set of polyhedra that can be generated from the Catalan solid
Catalan solid
In mathematics, a Catalan solid, or Archimedean dual, is a dual polyhedron to an Archimedean solid. The Catalan solids are named for the Belgian mathematician, Eugène Catalan, who first described them in 1865....
s. These have two types of vertices which can be alternately truncated. Truncating the "higher order" vertices and both vertex types produce these forms:
| Name | Original | Truncation | Full Truncation | Truncated name |
|---|---|---|---|---|
| Cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... Dual of rectified tetrahedron |
 |
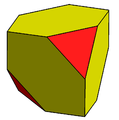 |
 |
Alternate truncated cube |
| Rhombic dodecahedron Rhombic dodecahedron In geometry, the rhombic dodecahedron is a convex polyhedron with 12 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. Its dual is the cuboctahedron.-Properties:... Dual of cuboctahedron |
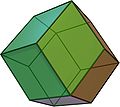 |
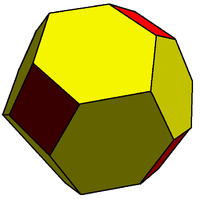 |
Truncated rhombic dodecahedron Truncated rhombic dodecahedron The truncated rhombic dodecahedron is a convex polyhedron constructed from the rhombic dodecahedron by truncating the 6 vertices.The 6 vertices are truncated such that all edges are equal length. The original 12 rhombic faces become flattened hexagons, and the truncated vertices become squares.The... |
|
| Rhombic triacontahedron Rhombic triacontahedron In geometry, the rhombic triacontahedron is a convex polyhedron with 30 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. It is the polyhedral dual of the icosidodecahedron, and it is a zonohedron.... Dual of icosidodecahedron |
 |
 |
Truncated rhombic triacontahedron Truncated rhombic triacontahedron The truncated rhombic triacontahedron is a convex polyhedron constructed as a truncation of the rhombic triacontahedron. It can more accurately be called a pentatruncated rhombic triacontahedron because only the order-5 vertices are truncated.... |
|
| Triakis tetrahedron Triakis tetrahedron In geometry, a triakis tetrahedron is an Archimedean dual solid, or a Catalan solid. Its dual is the truncated tetrahedron.It can be seen as a tetrahedron with triangular pyramids added to each face; that is, it is the Kleetope of the tetrahedron... Dual of truncated tetrahedron |
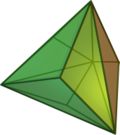 |
 |
Truncated triakis tetrahedron Truncated triakis tetrahedron The truncated triakis tetrahedron is a convex polyhedron with 16 faces: 4 sets of 3 pentagons arranged in a tetrahedral arrangement, with 4 hexagons in the gaps. It is constructed from taking a triakis tetrahedron by truncating the order-6 vertices... |
|
| Triakis octahedron Triakis octahedron In geometry, a triakis octahedron is an Archimedean dual solid, or a Catalan solid. Its dual is the truncated cube.It can be seen as an octahedron with triangular pyramids added to each face; that is, it is the Kleetope of the octahedron. It is also sometimes called a trisoctahedron, or, more... Dual of truncated cube |
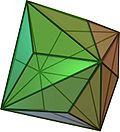 |
Truncated triakis octahedron | ||
| Triakis icosahedron Triakis icosahedron In geometry, the triakis icosahedron is an Archimedean dual solid, or a Catalan solid. Its dual is the truncated dodecahedron.It can be seen as an icosahedron with triangular pyramids augmented to each face; that is, it is the Kleetope of the icosahedron... Dual of truncated dodecahedron |
 |
Truncated triakis icosahedron |
Higher dimensions
This alternation operation applies to higher dimensional polytopes and honeycombs as well, however in general most forms won't have uniform solution. The voids created by the deleted vertices will not in general create uniform facets.Examples:
- HoneycombsHoneycomb (geometry)In geometry, a honeycomb is a space filling or close packing of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions....
- An alternated cubic honeycombCubic honeycombThe cubic honeycomb is the only regular space-filling tessellation in Euclidean 3-space, made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron....
is the tetrahedral-octahedral honeycombTetrahedral-octahedral honeycombThe tetrahedral-octahedral honeycomb or alternated cubic honeycomb is a space-filling tessellation in Euclidean 3-space. It is composed of alternating octahedra and tetrahedra in a ratio of 1:2....
. - An alternated hexagonal prismatic honeycombHexagonal prismatic honeycombThe hexagonal prismatic honeycomb is a space-filling tessellation in Euclidean 3-space made up of hexagonal prisms.It is constructed from a hexagonal tiling extruded into prisms.It is one of 28 convex uniform honeycombs.- References :...
is the gyrated alternated cubic honeycomb.
- An alternated cubic honeycomb
- PolychoraPolychoronIn geometry, a polychoron or 4-polytope is a four-dimensional polytope. It is a connected and closed figure, composed of lower dimensional polytopal elements: vertices, edges, faces , and cells...
- An alternated truncated 24-cellTruncated 24-cellIn geometry, a truncated 5-cell is a uniform polychoron formed as the truncation of the regular 5-cell.There are two degrees of trunctions, including a bitruncation.- Truncated 5-cell:...
is the snub 24-cellSnub 24-cellIn geometry, the snub 24-cell is a convex uniform polychoron composed of 120 regular tetrahedral and 24 icosahedral cells. Five tetrahedra and three icosahedra meet at each vertex. In total it has 480 triangular faces, 432 edges, and 96 vertices....
.
- An alternated truncated 24-cell
- A hypercubeHypercubeIn geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
can always be alternated into a uniform demihypercube.- CubeCubeIn geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
→ TetrahedronTetrahedronIn geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
(regular)-
 →
→ 
-
- Tesseract (8-cell) → 16-cell16-cellIn four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century....
(regular)-
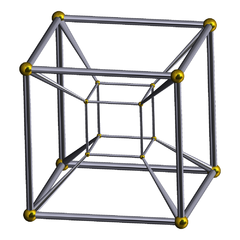 →
→ 
-
- PenteractPenteractIn five dimensional geometry, a 5-cube is a name for a five dimensional hypercube with 32 vertices, 80 edges, 80 square faces, 40 cubic cells, and 10 tesseract hypercells....
→ demipenteractDemipenteractIn five dimensional geometry, a demipenteract or 5-demicube is a semiregular 5-polytope, constructed from a 5-hypercube with alternated vertices deleted.It was discovered by Thorold Gosset...
(semiregular) - HexeractHexeractIn geometry, a 6-cube is a six-dimensional hypercube with 64 vertices, 192 edges, 240 square faces, 160 cubic cells, 60 tesseract 4-faces, and 12 5-cube 5-faces....
→ demihexeractDemihexeractIn geometry, a 6-demicube or demihexteract is a uniform 6-polytope, constructed from a 6-cube with alternate vertices deleted. It is part of a dimensionally infinite family of uniform polytopes called demihypercubes....
(uniform) - ...
- Cube
See also
- Other operators on uniform polytopes:
- Truncation (geometry)Truncation (geometry)In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :...
- Rectification (geometry)Rectification (geometry)In Euclidean geometry, rectification is the process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points...
- Omnitruncation (geometry)Omnitruncation (geometry)In geometry, an omnitruncation is an operation applied to a regular polytope in a Wythoff construction that creates a maximum number of facets...
- Cantellation (geometry)Cantellation (geometry)In geometry, a cantellation is an operation in any dimension that cuts a regular polytope at its edges and vertices, creating a new facet in place of each edge and vertex. The operation also applies to regular tilings and honeycombs...
- Runcination (geometry)
- Truncation (geometry)
- Conway polyhedral notation
- Wythoff constructionWythoff constructionIn geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.- Construction process :...
- Chiral polytopeChiral polytopeIn mathematics, a polytope P is chiral if it hastwo orbits of flags under its group of symmetries, withadjacent flags in different orbits.- References :* Schulte, E. Chiral polytopes in ordinary space, I. Discrete Comput. Geom. 32 , 55–99....

