.gif)
Prism (geometry)
Encyclopedia
| Set of uniform prisms | |
|---|---|
 (A hexagonal prism is shown) |
|
| Type | uniform polyhedron Uniform polyhedron A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive... |
| Faces | 2+n total: 2 {n} Regular polygon A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:... n {4} Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles... |
| Edges | 3n |
| Vertices | 2n |
| Schläfli symbol | {p}x{} or t{2, n} |
| Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
|
| Vertex configuration Vertex configuration In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron... |
4.4.n |
| Symmetry group | Dnh Dihedral symmetry in three dimensions This article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:... , [n,2], (*22n), order 2n |
| Dual polyhedron Dual polyhedron In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another... |
bipyramid Bipyramid An n-gonal bipyramid or dipyramid is a polyhedron formed by joining an n-gonal pyramid and its mirror image base-to-base.The referenced n-gon in the name of the bipyramids is not an external face but an internal one, existing on the primary symmetry plane which connects the two pyramid halves.The... s |
| Properties | convex, semi-regular vertex-transitive Vertex-transitive In geometry, a polytope is isogonal or vertex-transitive if, loosely speaking, all its vertices are the same... |
 n-gonal prism net (n = 9 here) Net (polyhedron) In geometry the net of a polyhedron is an arrangement of edge-joined polygons in the plane which can be folded to become the faces of the polyhedron... |
|
In geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a prism is a polyhedron
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
with an n-sided polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
al base, a translated
Translation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
copy (not in the same plane as the first), and n other faces (necessarily all parallelogram
Parallelogram
In Euclidean geometry, a parallelogram is a convex quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure...
s) joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a pentagonal prism. The prisms are a subclass of the prismatoid
Prismatoid
In geometry, a prismatoid is a polyhedron where all vertices lie in two parallel planes....
s.
General, right and uniform prisms
A right prism is a prism in which the joining edges and faces are perpendicular to the base faces. This applies if the joining faces are rectangular. If the joining edges and faces are not perpendicular to the base faces, it is called an oblique prism.Some texts may apply the term rectangular prism or square prism to both a right rectangular-sided prism and a right square-sided prism.
The term uniform prism can be used for a right prism with square sides, since such prisms are in the set of uniform polyhedra
Uniform polyhedron
A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
.
An n-prism, having regular polygon
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
ends and rectangular
Rectangle
In Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle...
sides, approaches a cylindrical
Cylinder (geometry)
A cylinder is one of the most basic curvilinear geometric shapes, the surface formed by the points at a fixed distance from a given line segment, the axis of the cylinder. The solid enclosed by this surface and by two planes perpendicular to the axis is also called a cylinder...
solid as n approaches infinity
Infinity
Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
.
Right prisms with regular bases and equal edge lengths form one of the two infinite series of semiregular polyhedra
Semiregular polyhedron
The term semiregular polyhedron is used variously by different authors.In its original definition, it is a polyhedron with regular faces and a symmetry group which is transitive on its vertices, which is more commonly referred to today as a uniform polyhedron...
, the other series being the antiprism
Antiprism
In geometry, an n-sided antiprism is a polyhedron composed of two parallel copies of some particular n-sided polygon, connected by an alternating band of triangles...
s.
The dual
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
of a right prism is a bipyramid
Bipyramid
An n-gonal bipyramid or dipyramid is a polyhedron formed by joining an n-gonal pyramid and its mirror image base-to-base.The referenced n-gon in the name of the bipyramids is not an external face but an internal one, existing on the primary symmetry plane which connects the two pyramid halves.The...
.
A parallelepiped
Parallelepiped
In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms. By analogy, it relates to a parallelogram just as a cube relates to a square. In Euclidean geometry, its definition encompasses all four concepts...
is a prism of which the base is a parallelogram
Parallelogram
In Euclidean geometry, a parallelogram is a convex quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure...
, or equivalently a polyhedron with 6 faces which are all parallelograms.
A right rectangular prism is also called a cuboid
Cuboid
In geometry, a cuboid is a solid figure bounded by six faces, forming a convex polyhedron. There are two competing definitions of a cuboid in mathematical literature...
, or informally a rectangular box. A right square prism is simply a square box, and may also be called a square cuboid.
An equilateral square prism is not a cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
.
Volume
The volumeVolume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
of a prism is the product of the area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
of the base and the distance between the two base faces, or the height (in the case of a non-right prism, note that this means the perpendicular distance).
The volume is therefore:
where B is the base area and h is the height. The volume of a prism whose base is a regular n-sided polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
with side length s is therefore:
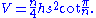
4 m
9 m
3 m
Symmetry
The symmetry groupSymmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
of a right n-sided prism with regular base is Dnh
Dihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
of order 4n, except in the case of a cube, which has the larger symmetry group Oh
Octahedral symmetry
150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation...
of order 47, which has three versions of D4h as subgroups. The rotation group
Rotation group
In mechanics and geometry, the rotation group is the group of all rotations about the origin of three-dimensional Euclidean space R3 under the operation of composition. By definition, a rotation about the origin is a linear transformation that preserves length of vectors and preserves orientation ...
is Dn of order 2n, except in the case of a cube, which has the larger symmetry group O of order 24, which has three versions of D4 as subgroups.
The symmetry group Dnh contains inversion iff
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
n is even.
Prismatic polytope
A prismatic polytopePolytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
is a dimensional generalization of a prism. An n-dimensional prismatic polytope is constructed from two (n − 1)-dimensional polytopes, translated into the next dimension.
The prismatic n-polytope elements are doubled from the (n − 1)-polytope elements and then creating new elements from the next lower element.
Take an n-polytope with fi i-face
Face
The face is a central sense organ complex, for those animals that have one, normally on the ventral surface of the head, and can, depending on the definition in the human case, include the hair, forehead, eyebrow, eyelashes, eyes, nose, ears, cheeks, mouth, lips, philtrum, temple, teeth, skin, and...
elements (i = 0, ,..., n). Its (n + 1)-polytope prism will have 2fi + fi−1 i-face elements. (With f−1 = 0, fn = 1.)
By dimension:
- Take a polygonPolygonIn geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
with n vertices, n edges. Its prism has 2n vertices, 3n edges, and 2 + n faces. - Take a polyhedronPolyhedronIn elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
with v vertices, e edges, and f faces. Its prism has 2v vertices, 2e + v edges, 2f + e faces, and 2 + f cells. - Take a polychoronPolychoronIn geometry, a polychoron or 4-polytope is a four-dimensional polytope. It is a connected and closed figure, composed of lower dimensional polytopal elements: vertices, edges, faces , and cells...
with v vertices, e edges, f faces and c cells. Its prism has 2v vertices, 2e + v edges, 2f + e faces, and 2c + f cells, and 2 + c hypercells.
Uniform prismatic polytope
A regular n-polytope represented by Schläfli symbol {p, q, ..., t} can form a uniform prismatic (n + 1)-polytope represented by a Cartesian productCartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of two Schläfli symbols: {p, q, ..., t}x{}.
By dimension:
- A 0-polytopic prism is a line segmentLine segmentIn geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
, represented by an empty Schläfli symbol {}. -
- A 1-polytopic prism is a rectangleRectangleIn Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle...
, made from 2 translated line segments. It is represented as the product Schläfli symbol {}x{}. If it is squareSquare (geometry)In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
, symmetry can be reduced it: {}x{} = {4}.-
Example: Square, {}x{}, two parallel line segments, connected by two line segment sides.
-
- A polygonPolygonIn geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
al prism is a 3-dimensional prism made from two translated polygons connected by rectangles. A regular polygon {p} can construct a uniform n-gonal prism represented by the product {p}x{}. If p = 4, with square sides symmetry it becomes a cubeCubeIn geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
: {2}x{} = {4, 3}.-
Example: Pentagonal prismPentagonal prismIn geometry, the pentagonal prism is a prism with a pentagonal base. It is a type of heptahedron with 7 faces, 15 edges, and 10 vertices.- As a semiregular polyhedron :...
, {5}x{}, two parallel pentagonPentagonIn geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...
s connected by 5 rectangular sides.
-
- A polyhedralPolyhedronIn elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
prism is a 4-dimensional prism made from two translated polyhedra connected by 3-dimensional prism cells. A regular polyhedron {p, q} can construct the uniform polychoric prism, represented by the product {p, q}x{}. If the polyhedron is a cube, and the sides are cubes, it becomes a tesseractTesseractIn geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8...
: {4, 3}x{} = {4, 3, 3}.-
Example: Dodecahedral prism, {5, 3}x{}, two parallel dodecahedra connected by 12 pentagonal prism sides.
-
- ...
Higher order prismatic polytopes also exist as Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
s of any two polytopes. The dimension of a polytope is the product of the dimensions of the elements. The first example of these exist in 4-dimensional space are called duoprism
Duoprism
In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher...
s as the product of two polygons. Regular duoprisms are represented as {p}×{q}.
External links
- Nonconvex Prisms and Antiprisms
- Surface Area MATHguide
- Volume MATHguide
- Paper models of prisms and antiprisms Free nets of prisms and antiprisms
- Paper models of prisms and antiprisms Using nets generated by StellaStella (software)Stella, a computer program available in three versions was created by Robert Webb of Australia...
. - Stella: Polyhedron Navigator: Software used to create the 3D and 4D images on this page.