
Rhombic dodecahedron
Encyclopedia
In geometry
, the rhombic dodecahedron is a convex polyhedron
with 12 rhombic
faces. It is an Archimedean dual
solid, or a Catalan solid
. Its dual
is the cuboctahedron
.
. Its polyhedral dual
is the cuboctahedron
. The long diagonal of each face is exactly √2 times the length of the short diagonal, so that the acute angles on each face measure cos−1(1/3), or approximately 70.53°.
Being the dual of an Archimedean polyhedron
, the rhombic dodecahedron is face-transitive, meaning the symmetry group
of the solid acts transitively on the set of faces. In elementary terms, this means that for any two faces A and B there is a rotation
or reflection
of the solid that leaves it occupying the same region of space while moving face A to face B.
The rhombic dodecahedron is one of the nine edge-transitive convex polyhedra, the others being the five Platonic solid
s, the cuboctahedron
, the icosidodecahedron
and the rhombic triacontahedron
.
The rhombic dodecahedron can be used to tessellate
3-dimensional space. It can be stacked to fill a space much like hexagons fill a plane.
This tessellation can be seen as the Voronoi tessellation of the face-centred cubic lattice
. Some minerals such as garnet
form a rhombic dodecahedral crystal habit
. Honeybees use the geometry of rhombic dodecahedra to form honeycomb
from a tessellation of cells each of which is a hexagonal prism
capped with half a rhombic dodecahedron. The rhombic dodecahedron also appears in the unit cells of diamond
and diamondoid
s. In these cases, four vertices are absent, but the chemical bonds lie on the remaining edges.
of an inscribed sphere
(tangent
to each of the rhombic dodecahedron's faces) is
the radius of the midsphere
is
and the radius of the circumscribed sphere
is


The coordinates of the six vertices where four faces meet at their acute angles are the permutations of:
symmetry. The cube can be seen as a rhombic hexahedron where the rhombi are squares.
Similarly it relates to the infinite series of tilings with the face configuration
s V3.2n.3.2n, the first in the Euclidean plane, and the rest in the hyperbolic plane.
:

 The rhombic dodecahedron forms the hull of the vertex-first projection of a tesseract
The rhombic dodecahedron forms the hull of the vertex-first projection of a tesseract
to 3 dimensions. There are exactly two ways of decomposing a rhombic dodecahedron into 4 congruent parallelepiped
s, giving 8 possible parallelepipeds. The 8 cells of the tesseract under this projection map precisely to these 8 parallelepipeds.
The rhombic dodecahedron forms the maximal cross-section of a 24-cell, and also forms the hull of its vertex-first parallel projection into 3 dimensions. The rhombic dodecahedron can be decomposed into 6 congruent (but non-regular) square dipyramids meeting at a single vertex in the center; these form the images of 6 pairs of the 24-cell's octahedral cells. The remaining 12 octahedral cells project onto the faces of the rhombic dodecahedron. The non-regularity of these images are due to projective distortion; the facets of the 24-cell are regular octahedra in 4-space.
This decomposition gives an interesting method for constructing the rhombic dodecahedron: cut a cube
into 6 congruent square pyramids, and attach them to the faces of a second cube. The triangular faces of each pair of adjacent pyramids lie on the same plane, and so merge into rhombuses. The 24-cell may also be constructed in an analogous way using two tesseract
s.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the rhombic dodecahedron is a convex polyhedron
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
with 12 rhombic
Rhombus
In Euclidean geometry, a rhombus or rhomb is a convex quadrilateral whose four sides all have the same length. The rhombus is often called a diamond, after the diamonds suit in playing cards, or a lozenge, though the latter sometimes refers specifically to a rhombus with a 45° angle.Every...
faces. It is an Archimedean dual
Archimedean solid
In geometry an Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices...
solid, or a Catalan solid
Catalan solid
In mathematics, a Catalan solid, or Archimedean dual, is a dual polyhedron to an Archimedean solid. The Catalan solids are named for the Belgian mathematician, Eugène Catalan, who first described them in 1865....
. Its dual
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
is the cuboctahedron
Cuboctahedron
In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...
.
Properties
The rhombic dodecahedron is a zonohedronZonohedron
A zonohedron is a convex polyhedron where every face is a polygon with point symmetry or, equivalently, symmetry under rotations through 180°. Any zonohedron may equivalently be described as the Minkowski sum of a set of line segments in three-dimensional space, or as the three-dimensional...
. Its polyhedral dual
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
is the cuboctahedron
Cuboctahedron
In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...
. The long diagonal of each face is exactly √2 times the length of the short diagonal, so that the acute angles on each face measure cos−1(1/3), or approximately 70.53°.
Being the dual of an Archimedean polyhedron
Archimedean solid
In geometry an Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices...
, the rhombic dodecahedron is face-transitive, meaning the symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
of the solid acts transitively on the set of faces. In elementary terms, this means that for any two faces A and B there is a rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
or reflection
Reflection (mathematics)
In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
of the solid that leaves it occupying the same region of space while moving face A to face B.
The rhombic dodecahedron is one of the nine edge-transitive convex polyhedra, the others being the five Platonic solid
Platonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
s, the cuboctahedron
Cuboctahedron
In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...
, the icosidodecahedron
Icosidodecahedron
In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon...
and the rhombic triacontahedron
Rhombic triacontahedron
In geometry, the rhombic triacontahedron is a convex polyhedron with 30 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. It is the polyhedral dual of the icosidodecahedron, and it is a zonohedron....
.
The rhombic dodecahedron can be used to tessellate
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
3-dimensional space. It can be stacked to fill a space much like hexagons fill a plane.
This tessellation can be seen as the Voronoi tessellation of the face-centred cubic lattice
Crystal structure
In mineralogy and crystallography, crystal structure is a unique arrangement of atoms or molecules in a crystalline liquid or solid. A crystal structure is composed of a pattern, a set of atoms arranged in a particular way, and a lattice exhibiting long-range order and symmetry...
. Some minerals such as garnet
Garnet
The garnet group includes a group of minerals that have been used since the Bronze Age as gemstones and abrasives. The name "garnet" may come from either the Middle English word gernet meaning 'dark red', or the Latin granatus , possibly a reference to the Punica granatum , a plant with red seeds...
form a rhombic dodecahedral crystal habit
Crystal habit
Crystal habit is an overall description of the visible external shape of a mineral. This description can apply to an individual crystal or an assembly of crystals or aggregates....
. Honeybees use the geometry of rhombic dodecahedra to form honeycomb
Honeycomb
A honeycomb is a mass of hexagonal waxcells built by honey bees in their nests to contain their larvae and stores of honey and pollen.Beekeepers may remove the entire honeycomb to harvest honey...
from a tessellation of cells each of which is a hexagonal prism
Hexagonal prism
In geometry, the hexagonal prism is a prism with hexagonal base. The shape has 8 faces, 18 edges, and 12 vertices.Since it has eight faces, it is an octahedron. However, the term octahedron is primarily used to refer to the regular octahedron, which has eight triangular faces...
capped with half a rhombic dodecahedron. The rhombic dodecahedron also appears in the unit cells of diamond
Diamond
In mineralogy, diamond is an allotrope of carbon, where the carbon atoms are arranged in a variation of the face-centered cubic crystal structure called a diamond lattice. Diamond is less stable than graphite, but the conversion rate from diamond to graphite is negligible at ambient conditions...
and diamondoid
Diamondoid
A diamondoid, in the context of building materials for nanotechnology components, most generally refers to structures that resemble diamond in a broad sense: namely, strong, stiff structures containing dense, 3-D networks of covalent bonds, formed chiefly from first and second row atoms with a...
s. In these cases, four vertices are absent, but the chemical bonds lie on the remaining edges.
Dimensions
If the edge length of a rhombic dodecahedron is a, the radiusRadius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
of an inscribed sphere
Inscribed sphere
In geometry, the inscribed sphere or insphere of a convex polyhedron is a sphere that is contained within the polyhedron and tangent to each of the polyhedron's faces...
(tangent
Tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
to each of the rhombic dodecahedron's faces) is
the radius of the midsphere
Midsphere
In geometry, the midsphere or intersphere of a polyhedron is a sphere which is tangent to every edge of the polyhedron. That is to say, it touches any given edge at exactly one point...
is
-
 .
.
and the radius of the circumscribed sphere
Circumscribed sphere
In geometry, a circumscribed sphere of a polyhedron is a sphere that contains the polyhedron and touches each of the polyhedron's vertices. The word circumsphere is sometimes used to mean the same thing...
is
-
 .
.
Area and volume
The area A and the volume V of the rhombic dodecahedron of edge length a are:

Cartesian coordinates
The eight vertices where three faces meet at their obtuse angles have Cartesian coordinates:- (±1, ±1, ±1)
The coordinates of the six vertices where four faces meet at their acute angles are the permutations of:
- (0, 0, ±2)
Related polyhedra
This polyhedron is a part of a sequence of rhombic polyhedra and tilings with [n,3] Coxeter groupCoxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
symmetry. The cube can be seen as a rhombic hexahedron where the rhombi are squares.
| Polyhedra | Euclidean tiling | Hyperbolic tiling | |||
|---|---|---|---|---|---|
| [3,3] | [4,3] | [5,3] | [6,3] | [7,3] | [8,3] |
 Cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
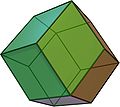 Rhombic dodecahedron Rhombic dodecahedron In geometry, the rhombic dodecahedron is a convex polyhedron with 12 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. Its dual is the cuboctahedron.-Properties:... |
 Rhombic triacontahedron Rhombic triacontahedron In geometry, the rhombic triacontahedron is a convex polyhedron with 30 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. It is the polyhedral dual of the icosidodecahedron, and it is a zonohedron.... |
Rhombille |
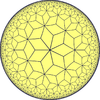 |
Similarly it relates to the infinite series of tilings with the face configuration
Face configuration
In geometry, a face configuration is notational description of a face-transitive polyhedron. It represents a sequential count of the number of faces that exist at each vertex around a face....
s V3.2n.3.2n, the first in the Euclidean plane, and the rest in the hyperbolic plane.
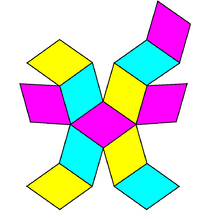 V3.4.3.4 (Drawn as a net Net (polyhedron) In geometry the net of a polyhedron is an arrangement of edge-joined polygons in the plane which can be folded to become the faces of the polyhedron... ) |
 V3.6.3.6 Euclidean plane tiling Rhombille tiling |
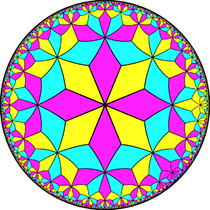 V3.8.3.8 Hyperbolic plane tiling (Drawn in a Poincaré disk model Poincaré disk model In geometry, the Poincaré disk model, also called the conformal disk model, is a model of n-dimensional hyperbolic geometry in which the points of the geometry are in an n-dimensional disk, or unit ball, and the straight lines of the hyperbolic geometry are segments of circles contained in the disk... ) |
Stellation
The stellated rhombic dodecahedron can be seen as a rhombic dodecahedron with rhombic-based pyramids augmented to each face, with a pyramid height extending the face planes of the neighboring faces:Honeycomb
The rhombic dodecahedron can tessellate space by translational copies of itselfRhombic dodecahedral honeycomb
The rhombic dodecahedra honeycomb is a space-filling tessellation in Euclidean 3-space. It is the Voronoi diagram of the face-centered cubic sphere-packing, which is believed to be the densest possible packing of equal spheres in ordinary space .It consists of copies of a single cell, the rhombic...
:

Related polytopes

Tesseract
In geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8...
to 3 dimensions. There are exactly two ways of decomposing a rhombic dodecahedron into 4 congruent parallelepiped
Parallelepiped
In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms. By analogy, it relates to a parallelogram just as a cube relates to a square. In Euclidean geometry, its definition encompasses all four concepts...
s, giving 8 possible parallelepipeds. The 8 cells of the tesseract under this projection map precisely to these 8 parallelepipeds.
The rhombic dodecahedron forms the maximal cross-section of a 24-cell, and also forms the hull of its vertex-first parallel projection into 3 dimensions. The rhombic dodecahedron can be decomposed into 6 congruent (but non-regular) square dipyramids meeting at a single vertex in the center; these form the images of 6 pairs of the 24-cell's octahedral cells. The remaining 12 octahedral cells project onto the faces of the rhombic dodecahedron. The non-regularity of these images are due to projective distortion; the facets of the 24-cell are regular octahedra in 4-space.
This decomposition gives an interesting method for constructing the rhombic dodecahedron: cut a cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
into 6 congruent square pyramids, and attach them to the faces of a second cube. The triangular faces of each pair of adjacent pyramids lie on the same plane, and so merge into rhombuses. The 24-cell may also be constructed in an analogous way using two tesseract
Tesseract
In geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8...
s.
See also
- Dodecahedron
- Rhombic triacontahedronRhombic triacontahedronIn geometry, the rhombic triacontahedron is a convex polyhedron with 30 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. It is the polyhedral dual of the icosidodecahedron, and it is a zonohedron....
- Rhombille tiling
- Truncated rhombic dodecahedronTruncated rhombic dodecahedronThe truncated rhombic dodecahedron is a convex polyhedron constructed from the rhombic dodecahedron by truncating the 6 vertices.The 6 vertices are truncated such that all edges are equal length. The original 12 rhombic faces become flattened hexagons, and the truncated vertices become squares.The...
- 24-cell - 4D analog of rhombic dodecahedron
- Rhombic dodecahedral honeycombRhombic dodecahedral honeycombThe rhombic dodecahedra honeycomb is a space-filling tessellation in Euclidean 3-space. It is the Voronoi diagram of the face-centered cubic sphere-packing, which is believed to be the densest possible packing of equal spheres in ordinary space .It consists of copies of a single cell, the rhombic...
External links
- Virtual Reality Polyhedra – The Encyclopedia of Polyhedra
Computer models
- Rhombic Dodecahedron -- interactive 3-d model
- Relating a Rhombic Triacontahedron and a Rhombic Dodecahedron, Rhombic Dodecahedron 5-Compound and Rhombic Dodecahedron 5-Compound by Sándor Kabai, The Wolfram Demonstrations Project.
Paper projects
- Rhombic Dodecahedron Calendar – make a rhombic dodecahedron calendar without glue
- Another Rhombic Dodecahedron Calendar – made by plaiting paper strips
Practical applications
- Archimede Institute Examples of actual housing construction projects using this geometry


