
Rhombic triacontahedron
Encyclopedia
In geometry
, the rhombic triacontahedron is a convex polyhedron
with 30 rhombic
faces. It is an Archimedean dual
solid, or a Catalan solid
. It is the polyhedral dual
of the icosidodecahedron
, and it is a zonohedron
.
The ratio of the long diagonal to the short diagonal of each face is exactly equal to the golden ratio
, φ, so that the acute angles on each face measure 2 tan−1(1/φ) = tan−1(2), or approximately 63.43°.
A rhombus so obtained is called a golden rhombus.
Being the dual of an Archimedean polyhedron
, the rhombic triacontahedron is face-transitive, meaning the symmetry group
of the solid acts transitively on the set of faces. In elementary terms, this means that for any two faces A and B there is a rotation
or reflection
of the solid that leaves it occupying the same region of space while moving face A to face B. The rhombic triacontahedron is also somewhat special in being one of the nine edge-transitive convex polyhedra, the others being the five Platonic solid
s, the cuboctahedron
, the icosidodecahedron
, and the rhombic dodecahedron
.
The rhombic triacontahedron is also interesting in that it has all the vertices of an icosahedron
, a dodecahedron, a hexahedron
, and a tetrahedron
.
Woodworker Jane Kostick builds boxes in the shape of a rhombic triacontahedron. The simple construction is based on the less than obvious relationship between the rhombic triacontahedron and the cube.
Roger von Oech's "Ball of Whacks" comes in the shape of a rhombic triacontahedron.
In some roleplaying games, and for elementary school
uses, the rhombic triacontahedron is used as the "d30" thirty-sided dice.
symmetry. The cube can be seen as a rhombic hexahedron where the rhombi are also rectangles.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the rhombic triacontahedron is a convex polyhedron
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
with 30 rhombic
Rhombus
In Euclidean geometry, a rhombus or rhomb is a convex quadrilateral whose four sides all have the same length. The rhombus is often called a diamond, after the diamonds suit in playing cards, or a lozenge, though the latter sometimes refers specifically to a rhombus with a 45° angle.Every...
faces. It is an Archimedean dual
Archimedean solid
In geometry an Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices...
solid, or a Catalan solid
Catalan solid
In mathematics, a Catalan solid, or Archimedean dual, is a dual polyhedron to an Archimedean solid. The Catalan solids are named for the Belgian mathematician, Eugène Catalan, who first described them in 1865....
. It is the polyhedral dual
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
of the icosidodecahedron
Icosidodecahedron
In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon...
, and it is a zonohedron
Zonohedron
A zonohedron is a convex polyhedron where every face is a polygon with point symmetry or, equivalently, symmetry under rotations through 180°. Any zonohedron may equivalently be described as the Minkowski sum of a set of line segments in three-dimensional space, or as the three-dimensional...
.
The ratio of the long diagonal to the short diagonal of each face is exactly equal to the golden ratio
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
, φ, so that the acute angles on each face measure 2 tan−1(1/φ) = tan−1(2), or approximately 63.43°.
A rhombus so obtained is called a golden rhombus.
Being the dual of an Archimedean polyhedron
Archimedean solid
In geometry an Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices...
, the rhombic triacontahedron is face-transitive, meaning the symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
of the solid acts transitively on the set of faces. In elementary terms, this means that for any two faces A and B there is a rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
or reflection
Reflection (mathematics)
In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
of the solid that leaves it occupying the same region of space while moving face A to face B. The rhombic triacontahedron is also somewhat special in being one of the nine edge-transitive convex polyhedra, the others being the five Platonic solid
Platonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
s, the cuboctahedron
Cuboctahedron
In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...
, the icosidodecahedron
Icosidodecahedron
In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon...
, and the rhombic dodecahedron
Rhombic dodecahedron
In geometry, the rhombic dodecahedron is a convex polyhedron with 12 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. Its dual is the cuboctahedron.-Properties:...
.
The rhombic triacontahedron is also interesting in that it has all the vertices of an icosahedron
Icosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
, a dodecahedron, a hexahedron
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
, and a tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
.
Uses of rhombic triacontahedra
Danish designer Holger Strøm used the rhombic triacontahedron as a basis for the design of his buildable lamp IQ-light. (IQ for "Interlocking Quadrilaterals")Woodworker Jane Kostick builds boxes in the shape of a rhombic triacontahedron. The simple construction is based on the less than obvious relationship between the rhombic triacontahedron and the cube.
Roger von Oech's "Ball of Whacks" comes in the shape of a rhombic triacontahedron.
In some roleplaying games, and for elementary school
Elementary school
An elementary school or primary school is an institution where children receive the first stage of compulsory education known as elementary or primary education. Elementary school is the preferred term in some countries, particularly those in North America, where the terms grade school and grammar...
uses, the rhombic triacontahedron is used as the "d30" thirty-sided dice.
Related polyhedra
This polyhedron is a part of a sequence of rhombic polyhedra and tilings with [n,3] Coxeter groupCoxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
symmetry. The cube can be seen as a rhombic hexahedron where the rhombi are also rectangles.
| Polyhedra | Euclidean tiling | Hyperbolic tiling | |||
|---|---|---|---|---|---|
| [3,3] | [4,3] | [5,3] | [6,3] | [7,3] | [8,3] |
 Cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
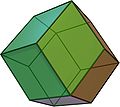 Rhombic dodecahedron Rhombic dodecahedron In geometry, the rhombic dodecahedron is a convex polyhedron with 12 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. Its dual is the cuboctahedron.-Properties:... |
 Rhombic triacontahedron Rhombic triacontahedron In geometry, the rhombic triacontahedron is a convex polyhedron with 30 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. It is the polyhedral dual of the icosidodecahedron, and it is a zonohedron.... |
Rhombille |
 |
External links
- Rhombic Triacontrahedron -- Interactive Polyhedron Model
- Virtual Reality Polyhedra – The Encyclopedia of Polyhedra
- Stellations of Rhombic Triacontahedron
- IQ-light–Danish designer Holger Strøm's lamp
- Make your own
- a wooden construction of a rhombic triacontahedron box – by woodworker Jane Kostick
- 120 Rhombic Triacontahedra, 30+12 Rhombic Triacontahedra, and 12 Rhombic Triacontahedra by Sándor Kabai, The Wolfram Demonstrations Project.

