Antiprism - AbsoluteAstronomy.com

Set of uniform antiprisms

Type	uniform polyhedron Uniform polyhedron A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
Faces	2 n-gon Polygon In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments... s, 2n triangle Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... s
Edges	4n
Vertices	2n
Vertex configuration Vertex configuration In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron...	3.3.3.n
Schläfli symbol	h_0,1{2,2n} s{2,n}
Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... s
Symmetry group	D_nd, [2⁺,2n], (2*n), order 4n D_n, [2,n]⁺, (22n), order 2n
Dual polyhedron Dual polyhedron In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...	trapezohedron Trapezohedron The n-gonal trapezohedron, antidipyramid or deltohedron is the dual polyhedron of an n-gonal antiprism. Its 2n faces are congruent kites . The faces are symmetrically staggered.The n-gon part of the name does not reference the faces here but arrangement of vertices around an axis of symmetry...
Properties	convex, semi-regular vertex-transitive Vertex-transitive In geometry, a polytope is isogonal or vertex-transitive if, loosely speaking, all its vertices are the same...
Net Net (polyhedron) In geometry the net of a polyhedron is an arrangement of edge-joined polygons in the plane which can be folded to become the faces of the polyhedron...

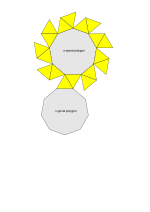In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, an n-sided antiprism is a polyhedron

Polyhedron

In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...

composed of two parallel copies of some particular n-sided polygon

Polygon

In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...

, connected by an alternating band of triangle

Triangle

A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....

s. Antiprisms are a subclass of the prismatoid

Prismatoid

In geometry, a prismatoid is a polyhedron where all vertices lie in two parallel planes....

s.

Antiprisms are similar to prism

Prism (geometry)

In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...

s except the bases are twisted relative to each other, and that the side faces are triangles, rather than quadrilaterals.

In the case of a regular n-sided base, one usually considers the case where its copy is twisted by an angle 180°/n. Extra regularity is obtained by the line connecting the base centers being perpendicular to the base planes, making it a right antiprism. As faces, it has the two n-gonal bases and, connecting those bases, 2n isosceles triangles.

Uniform antiprism

A uniform
Prismatic uniform polyhedron
In geometry, a prismatic uniform polyhedron is a uniform polyhedron with dihedral symmetry. They exist in two infinite families, the uniform prisms and the uniform antiprisms...

antiprism has, apart from the base faces, 2n equilateral triangles as faces. As a class, the uniform antiprisms form an infinite series of vertex-uniform polyhedra, as do the uniform prisms. For n=2 we have as degenerate case the regular tetrahedron

Tetrahedron

In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...

, and for n=3 the non-degenerate regular octahedron

Octahedron

In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....

.

The dual polyhedra

Dual polyhedron

In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...

of the antiprisms are the trapezohedra

Trapezohedron

The n-gonal trapezohedron, antidipyramid or deltohedron is the dual polyhedron of an n-gonal antiprism. Its 2n faces are congruent kites . The faces are symmetrically staggered.The n-gon part of the name does not reference the faces here but arrangement of vertices around an axis of symmetry...

. Their existence was first discussed and their name was coined by Johannes Kepler

Johannes Kepler

Johannes Kepler was a German mathematician, astronomer and astrologer. A key figure in the 17th century scientific revolution, he is best known for his eponymous laws of planetary motion, codified by later astronomers, based on his works Astronomia nova, Harmonices Mundi, and Epitome of Copernican...

Cartesian coordinates

Cartesian coordinates for the vertices of a right antiprism with n-gonal bases and isosceles triangles are

with k ranging from 0 to 2n-1; if the triangles are equilateral,

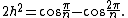
Volume and surface area

Let

be the edge-length of a uniform

Uniform polyhedron

A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...

antiprism. Then the volume is

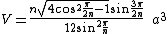
and the surface area is

Symmetry

The symmetry group

Symmetry group

The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...

of a right n-sided antiprism with regular base and isosceles side faces is D_nd of order 4n, except in the case of a tetrahedron, which has the larger symmetry group T_d of order 24, which has three versions of D_2d as subgroups, and the octahedron, which has the larger symmetry group O_h of order 48, which has four versions of D_3d as subgroups.

The symmetry group contains inversion if and only if

If and only if

In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....

n is odd.

The rotation group

Rotation group

In mechanics and geometry, the rotation group is the group of all rotations about the origin of three-dimensional Euclidean space R3 under the operation of composition. By definition, a rotation about the origin is a linear transformation that preserves length of vectors and preserves orientation ...

is D_n of order 2n, except in the case of a tetrahedron, which has the larger rotation group T of order 12, which has three versions of D₂ as subgroups, and the octahedron, which has the larger rotation group O of order 24, which has four versions of D₃ as subgroups.

External links

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.

Uniform antiprism

Cartesian coordinates

Volume and surface area

Symmetry

See also

External links