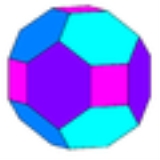
Truncated rhombic dodecahedron
Type	Conway polyhedron Conway polyhedron notation Conway polyhedron notation is used to describe polyhedra based on a seed polyhedron modified by various operations.The seed polyhedra are the Platonic solids, represented by their first letter of their name ; the prisms , antiprisms and pyramids...
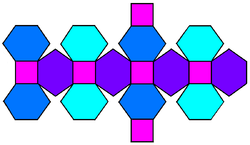
Faces	6 square Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles... s 12 hexagons
Edges	48 (2 types)
Vertices	32 (2 types)
Vertex configuration Vertex configuration In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron...	(24) 4.6.6 (8) 6.6.6
Symmetry group Symmetry group The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...	octahedral (Oh)
Dual polyhedron Dual polyhedron In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...	Tetrakis cuboctahedron Tetrakis cuboctahedron The tetrakis cuboctahedron is a convex polyhedron with 32 triangular faces, 48 edges, and 18 vertices. It a dual of the truncated rhombic dodecahedron....
Properties	convex Convex set In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object... , zonohedron Zonohedron A zonohedron is a convex polyhedron where every face is a polygon with point symmetry or, equivalently, symmetry under rotations through 180°. Any zonohedron may equivalently be described as the Minkowski sum of a set of line segments in three-dimensional space, or as the three-dimensional... , equilateral Equilateral In geometry, an equilateral polygon is a polygon which has all sides of the same length.For instance, an equilateral triangle is a triangle of equal edge lengths... -faced

The truncated rhombic dodecahedron is a convex

Convex polygon

In geometry, a polygon can be either convex or concave .- Convex polygons :A convex polygon is a simple polygon whose interior is a convex set...

 polyhedron

Polyhedron

In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...

 constructed from the rhombic dodecahedron

Rhombic dodecahedron

In geometry, the rhombic dodecahedron is a convex polyhedron with 12 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. Its dual is the cuboctahedron.-Properties:...

 by truncating

Truncation (geometry)

In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :...

 the 6 (order 4) vertices.

The 6 vertices are truncated such that all edges are equal length. The original 12 rhombic

Rhombus

In Euclidean geometry, a rhombus or rhomb is a convex quadrilateral whose four sides all have the same length. The rhombus is often called a diamond, after the diamonds suit in playing cards, or a lozenge, though the latter sometimes refers specifically to a rhombus with a 45° angle.Every...

 faces become flattened hexagons, and the truncated vertices become squares.

The hexagonal faces are equilateral

Equilateral

In geometry, an equilateral polygon is a polygon which has all sides of the same length.For instance, an equilateral triangle is a triangle of equal edge lengths...

 but not regular

Regular polygon

A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...

. They are formed by a truncated rhombus, have 2 internal angles of about 109.47 degrees (arccos(-1/3)) and 4 internal angles of about 125.26 degrees, while a regular hexagon would have all 120 degree angles.

Because all its faces have an even number of sides with 180 degree rotation symmetry, it is a zonohedron

Zonohedron

A zonohedron is a convex polyhedron where every face is a polygon with point symmetry or, equivalently, symmetry under rotations through 180°. Any zonohedron may equivalently be described as the Minkowski sum of a set of line segments in three-dimensional space, or as the three-dimensional...

.

The truncated rhombic dodecahedron is the Minkowski sum of a rhombic dodecahedron and a cube of side length 1 when
eight vertices of the rhombic dodecahedron are at 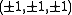and its
six vertices are at the permutations of .

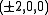Full truncation

The name truncated rhombic dodecahedron is ambiguous since only 6 vertices were truncated. A truncation on just the 3-vertices of the rhombic dodecahedron would cause an icosahedron with 12 equilateral hexagons and 20 triangles, forming 30 vertices in total; this figure's dual can be called the triakis cuboctahedron. Another alternate truncated rhombic dodecahedron can appear by truncating all 14 vertices, yielding 12 irregular octagonal faces. The dual of the full truncation is a triangular tetracontaoctahedron labeled the tritetrakis cuboctahedron, which is a complete Kleetope

Kleetope

In geometry and polyhedral combinatorics, the Kleetope of a polyhedron or higher-dimensional convex polytope is another polyhedron or polytope formed by replacing each facet of with a shallow pyramid...

 of the cuboctahedron

Cuboctahedron

In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...

. The tetrahedron

Tetrahedron

In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...

 is to the truncated cube

Truncated cube

In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices....

 as the cube

Cube

In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...

 is to the full truncation or a bitruncated cuboctahedron.

Similar polyhedra

This polyhedron is similar to the uniform truncated octahedron

Truncated octahedron

In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron....

:

Truncated rhombic dodecahedron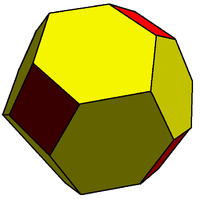	Truncated octahedron

This polyhedron is also a part of a sequence of truncated rhombic polyhedra and tilings with [n,3] Coxeter group

Coxeter group

In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...

 symmetry. The cube can be seen as a rhombic hexahedron where the rhombi are squares. The truncated forms have regular n-gons at the truncated vertices, and nonregular hexagonal faces. The sequence has two vertex figures (n.6.6) and (6,6,6). The hexagonal tiling can be considered a truncated rhombille tiling.

Polyhedra			Euclidean tiling	Hyperbolic tiling
[3,3]	[4,3]	[5,3]	[6,3]	[7,3]	[8,3]
Cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...	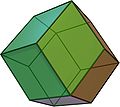Rhombic dodecahedron Rhombic dodecahedron In geometry, the rhombic dodecahedron is a convex polyhedron with 12 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. Its dual is the cuboctahedron.-Properties:...	Rhombic triacontahedron Rhombic triacontahedron In geometry, the rhombic triacontahedron is a convex polyhedron with 30 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. It is the polyhedral dual of the icosidodecahedron, and it is a zonohedron....	Rhombille
Alternate truncated cube	Truncated rhombic dodecahedron Truncated rhombic dodecahedron The truncated rhombic dodecahedron is a convex polyhedron constructed from the rhombic dodecahedron by truncating the 6 vertices.The 6 vertices are truncated such that all edges are equal length. The original 12 rhombic faces become flattened hexagons, and the truncated vertices become squares.The...	Truncated rhombic triacontahedron Truncated rhombic triacontahedron The truncated rhombic triacontahedron is a convex polyhedron constructed as a truncation of the rhombic triacontahedron. It can more accurately be called a pentatruncated rhombic triacontahedron because only the order-5 vertices are truncated....	Hexagonal tiling

External links

• http://unistates.com/rmt/explained/glossary/trd.html
• VRML
  VRML
  VRML is a standard file format for representing 3-dimensional interactive vector graphics, designed particularly with the World Wide Web in mind...
  
   model http://www.georgehart.com/virtual-polyhedra/vrml/zono-7_from_cube.wrl
  • VTML polyhedral generator Try "t4daC" (Conway polyhedron notation
    Conway polyhedron notation
    Conway polyhedron notation is used to describe polyhedra based on a seed polyhedron modified by various operations.The seed polyhedra are the Platonic solids, represented by their first letter of their name ; the prisms , antiprisms and pyramids...
    
    )