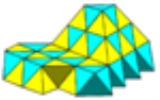
Tetrahedral-octahedral honeycomb
Encyclopedia
| Alternated cubic honeycomb | |
|---|---|
 |
|
| Type | Uniform honeycomb Convex uniform honeycomb In geometry, a convex uniform honeycomb is a uniform tessellation which fills three-dimensional Euclidean space with non-overlapping convex uniform polyhedral cells.Twenty-eight such honeycombs exist:* the familiar cubic honeycomb and 7 truncations thereof;... |
| Family | Alternated hypercubic honeycomb |
| Schläfli symbol | h0{4,3,4} {3[4]} |
| Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... s |
or |
| Cell types | {3,3} Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... , {3,4} Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
| Face types | triangle Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... {3} |
| Edge figure | [{3,3}.{3,4}]2 (rectangle Rectangle In Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle... ) |
| Vertex figure | 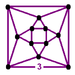 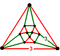  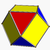 (cuboctahedron Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... ) |
| Cells/edge | [{3,3}.{3,4}]2 |
| Faces/edge | 4 {3} |
| Cells/vertex | {3,3} Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... 8+{3,4} Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... 6 |
| Faces/vertex | 24 {3} |
| Edges/vertex | 12 |
| Symmetry group Space group In mathematics and geometry, a space group is a symmetry group, usually for three dimensions, that divides space into discrete repeatable domains.In three dimensions, there are 219 unique types, or counted as 230 if chiral copies are considered distinct... |
Fmm |
| Coxeter group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... s |
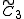 , [1+,4,3,4] , [1+,4,3,4]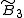 , [4,31,1] , [4,31,1] , [3[4]] , [3[4]] |
| Dual | rhombic dodecahedral honeycomb Rhombic dodecahedral honeycomb The rhombic dodecahedra honeycomb is a space-filling tessellation in Euclidean 3-space. It is the Voronoi diagram of the face-centered cubic sphere-packing, which is believed to be the densest possible packing of equal spheres in ordinary space .It consists of copies of a single cell, the rhombic... |
| Properties | vertex-transitive Vertex-transitive In geometry, a polytope is isogonal or vertex-transitive if, loosely speaking, all its vertices are the same... , edge-transitive, face-transitive |
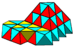
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
(or honeycomb
Honeycomb (geometry)
In geometry, a honeycomb is a space filling or close packing of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions....
) in Euclidean 3-space. It is composed of alternating octahedra
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
and tetrahedra
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
in a ratio of 1:2.
It is vertex-transitive with 8 tetrahedra and 6 octahedra around each vertex. It is edge-transitive with 2 tetrahedra and 2 octahedra alternating on each edge.
It is part of an infinite family of uniform tessellations called alternated hypercubic honeycombs, formed as an alternation of a hypercubic honeycomb and being composed of demihypercube and cross-polytope
Cross-polytope
In geometry, a cross-polytope, orthoplex, hyperoctahedron, or cocube is a regular, convex polytope that exists in any number of dimensions. The vertices of a cross-polytope are all the permutations of . The cross-polytope is the convex hull of its vertices...
facets.
In this case of 3-space, the cubic honeycomb
Cubic honeycomb
The cubic honeycomb is the only regular space-filling tessellation in Euclidean 3-space, made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron....
is alternated, reducing the cubic cells to tetrahedra, and the deleted vertices create octahedral voids. As such it can be represented by an extended Schläfli symbol h{4,3,4} as containing half the vertices of the {4,3,4} cubic honeycomb.
There's a similar honeycomb called gyrated tetrahedral-octahedral honeycomb
Gyrated tetrahedral-octahedral honeycomb
The gyrated tetrahedral-octahedral honeycomb or gyrated alternated cubic honeycomb is a space-filling tessellation in Euclidean 3-space made up of octahedra and tetrahedra in a ratio of 1:2....
which has layers rotated 60 degrees so half the edges have neighboring rather than alternating tetrahedra and octahedra.
This vertex arrangement
Vertex arrangement
In geometry, a vertex arrangement is a set of points in space described by their relative positions. They can be described by their use in polytopes....
is called the A3 lattice.
Images
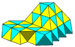
 Wireframe (perspective) |
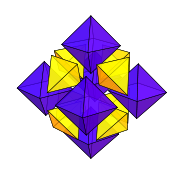 This diagram shows an exploded view Exploded view An exploded view drawing is a diagram, picture or technical drawing of an object, that shows the relationship or order of assembly of various parts.... of the cells surrounding each vertex. |
Projection by folding
The alternated cubic honeycomb can be orthogonally projected into the planar square tiling by a geometric folding operation that maps two pairs of mirrors into each other. The projection of the alternated cubic honeycomb creates two offset copies of the square tiling vertex arrangementVertex arrangement
In geometry, a vertex arrangement is a set of points in space described by their relative positions. They can be described by their use in polytopes....
of the plane:
| Coxeter group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... |
Coxeter diagram |
Graph |
|---|---|---|
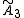 |
 alternated cubic honeycomb |
|
 |
 square tiling |

