Snub cube
Encyclopedia
In geometry
, the snub cube, or snub cuboctahedron, is an Archimedean solid
.
The snub cube has 38 faces, 6 of which are square
s and the other 32 are equilateral triangles. It has 60 edges
and 24 vertices
. It is a chiral
polyhedron, that is, it has two distinct forms, which are mirror image
s (or "enantiomorphs
") of each other. The only other chiral Archimedean solid is the snub dodecahedron
.
and its volume is 
, where 
is the tribonacci constant
.
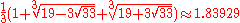If the original snub cube has edge length 1, its dual pentagonal icositetrahedron
has side lengths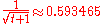
and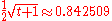 
.
of a snub cube are all the even permutations of
with an even number of plus signs, along with all the odd permutations with an odd number of plus signs, where ξ is the real solution to
which can be written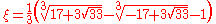
or approximately 0.543689. ξ is the reciprocal of the tribonacci constant
. Taking the even permutations with an odd number of plus signs, and the odd permutations with an even number of plus signs, gives a different snub cube, the mirror image.
This snub cube has edges of length α, a number which satisfies the equation
and can be written as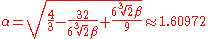
For a snub cube with unit edge length, use the following coordinates instead:
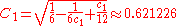
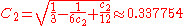
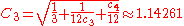--This formula is wrong, but the value correct.
so they no longer touch, then giving them each a small rotation on their centers (all clockwise or all counter-clockwise) until the spaces between can be filled with equilateral triangles.
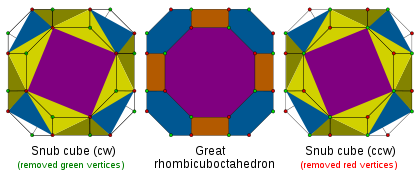
It can also be constructed as an alternation of a nonuniform omnitruncated cube
, deleting every other vertex and creating new triangles at the deleted vertices. A properly proportioned (nonuniform
) great rhombicuboctahedron will create equilateral triangles at the deleted vertices. Depending on which set of vertices are alternated, the resulting snub cube can have a clockwise or counterclockwise twist.
A "improved" snub cube, with a slightly smaller square face and slightly larger triangular faces compared to Archimedes' uniform snub cube, is useful as a spherical design
.
polyhedra and tilings with vertex figure (3.3.3.3.p) and Coxeter-Dynkin diagram
, which can be constructed as alternations of the omnitruncation sequence .
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the snub cube, or snub cuboctahedron, is an Archimedean solid
Archimedean solid
In geometry an Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices...
.
The snub cube has 38 faces, 6 of which are square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
s and the other 32 are equilateral triangles. It has 60 edges
Edge (geometry)
In geometry, an edge is a one-dimensional line segment joining two adjacent zero-dimensional vertices in a polygon. Thus applied, an edge is a connector for a one-dimensional line segment and two zero-dimensional objects....
and 24 vertices
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
. It is a chiral
Chirality (mathematics)
In geometry, a figure is chiral if it is not identical to its mirror image, or, more precisely, if it cannot be mapped to its mirror image by rotations and translations alone. For example, a right shoe is different from a left shoe, and clockwise is different from counterclockwise.A chiral object...
polyhedron, that is, it has two distinct forms, which are mirror image
Mirror image
A mirror image is a reflected duplication of an object that appears identical but reversed. As an optical effect it results from reflection off of substances such as a mirror or water. It is also a concept in geometry and can be used as a conceptualization process for 3-D structures...
s (or "enantiomorphs
Chirality (mathematics)
In geometry, a figure is chiral if it is not identical to its mirror image, or, more precisely, if it cannot be mapped to its mirror image by rotations and translations alone. For example, a right shoe is different from a left shoe, and clockwise is different from counterclockwise.A chiral object...
") of each other. The only other chiral Archimedean solid is the snub dodecahedron
Snub dodecahedron
In geometry, the snub dodecahedron, or snub icosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces....
.
Dimensions
For a snub cube with edge length 1, its surface area is and its volume is , where is the tribonacci constantGeneralizations of Fibonacci numbers
In mathematics, the Fibonacci numbers form a sequence defined recursively by:The Fibonacci sequence has been studied extensively and generalized in many ways, for example, by starting with other numbers than 0 and 1, by adding more than two numbers to generate the next number, or by adding objects...
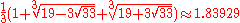.If the original snub cube has edge length 1, its dual pentagonal icositetrahedron
Pentagonal icositetrahedron
In geometry, a pentagonal icositetrahedron is a Catalan solid which is the dual of the snub cube. It has two distinct forms, which are mirror images of each other....
has side lengths
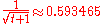and 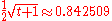.Cartesian coordinates
Cartesian coordinates for the verticesVertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
of a snub cube are all the even permutations of
- (±1, ±ξ, ±1/ξ)
with an even number of plus signs, along with all the odd permutations with an odd number of plus signs, where ξ is the real solution to
- ξ3+ξ2+ξ=1,
which can be written
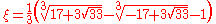
or approximately 0.543689. ξ is the reciprocal of the tribonacci constant
Generalizations of Fibonacci numbers
In mathematics, the Fibonacci numbers form a sequence defined recursively by:The Fibonacci sequence has been studied extensively and generalized in many ways, for example, by starting with other numbers than 0 and 1, by adding more than two numbers to generate the next number, or by adding objects...
. Taking the even permutations with an odd number of plus signs, and the odd permutations with an even number of plus signs, gives a different snub cube, the mirror image.
This snub cube has edges of length α, a number which satisfies the equation
- α6−4α4+16α2−32=0,
and can be written as
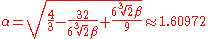
For a snub cube with unit edge length, use the following coordinates instead:
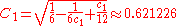
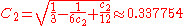
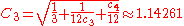--This formula is wrong, but the value correct.Geometric relations
The snub cube can be generated by taking the six faces of the cube, pulling them outwardExpansion (geometry)
In geometry, expansion is a polytope operation where facets are separated and moved radially apart, and new facets are formed at separated elements...
so they no longer touch, then giving them each a small rotation on their centers (all clockwise or all counter-clockwise) until the spaces between can be filled with equilateral triangles.
 Cube |
 Rhombicuboctahedron (Expanded cube) |
It can also be constructed as an alternation of a nonuniform omnitruncated cube
Truncated cuboctahedron
In geometry, the truncated cuboctahedron is an Archimedean solid. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices and 72 edges...
, deleting every other vertex and creating new triangles at the deleted vertices. A properly proportioned (nonuniform
Uniform polyhedron
A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
) great rhombicuboctahedron will create equilateral triangles at the deleted vertices. Depending on which set of vertices are alternated, the resulting snub cube can have a clockwise or counterclockwise twist.
A "improved" snub cube, with a slightly smaller square face and slightly larger triangular faces compared to Archimedes' uniform snub cube, is useful as a spherical design
Spherical design
A spherical design, part of combinatorial design theory in mathematics, is a finite set of N points on the d-dimensional unit hypersphere Sd such that the average value of any polynomial f of degree t or less on the set equals the average value of f on the whole sphere...
.
Related polyhedra and tilings
This semiregular polyhedron is part of sequence of snubbedSnub (geometry)
In geometry, an alternation is an operation on a polyhedron or tiling that removes alternate vertices. Only even-sided polyhedra can be alternated, for example the zonohedra. Every 2n-sided face becomes n-sided...
polyhedra and tilings with vertex figure (3.3.3.3.p) and Coxeter-Dynkin diagram
Coxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
, which can be constructed as alternations of the omnitruncation sequence .
| 232 | 332 | 432 | 532 | 632 | 732 | 832 |
|---|---|---|---|---|---|---|
 (4.6.4) Hexagonal prism In geometry, the hexagonal prism is a prism with hexagonal base. The shape has 8 faces, 18 edges, and 12 vertices.Since it has eight faces, it is an octahedron. However, the term octahedron is primarily used to refer to the regular octahedron, which has eight triangular faces... |
 (4.6.6) Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron.... |
 (4.6.8) Truncated cuboctahedron In geometry, the truncated cuboctahedron is an Archimedean solid. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices and 72 edges... |
 (4.6.10) Snub dodecahedron In geometry, the snub dodecahedron, or snub icosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces.... |
 4.6.12 |
 4.6.14 |
 4.6.16 |
 (3.3.3.3.2) |
 (3.3.3.3.3) Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... |
 (3.3.3.3.4) Snub cube In geometry, the snub cube, or snub cuboctahedron, is an Archimedean solid.The snub cube has 38 faces, 6 of which are squares and the other 32 are equilateral triangles. It has 60 edges and 24 vertices. It is a chiral polyhedron, that is, it has two distinct forms, which are mirror images of each... |
 (3.3.3.3.5) Snub dodecahedron In geometry, the snub dodecahedron, or snub icosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces.... |
 3.3.3.3.6 Snub hexagonal tiling In geometry, the Snub hexagonal tiling is a semiregular tiling of the Euclidean plane. There are four triangles and one hexagon on each vertex... |
 3.3.3.3.7 |
 3.3.3.3.8 |
External links
- The Uniform Polyhedra
- Virtual Reality Polyhedra The Encyclopedia of Polyhedra
- Editable printable net of a Snub Cube with interactive 3D view