
Truncated square tiling
Encyclopedia
In geometry
, the truncated square tiling is a semiregular tiling of the Euclidean plane. There is one square and two octagons on each vertex
. This is the only edge-to-edge tiling by regular convex polygons which contains an octagon. It has Schläfli symbol of t0,1{4,4}.
Conway
calls it a truncated quadrille, constructed as a truncation
operation applied to a square tiling (quadrille).
Other names used for this pattern include Mediterranean tiling and octagonal tiling.
There are 3 regular and 8 semiregular tilings in the plane.
s of a truncated square tiling. (Naming the colors by indices around a vertex (4.8.8): 122, 123.)
related to the polyhedron truncated octahedron
, 4.6.6.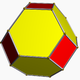
The Pythagorean tiling
alternates large and small squares, and may be seen as topologically identical to the truncated square tiling. The squares are rotated 45 degrees and octagons are distorted into squares with mid-edge vertices.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the truncated square tiling is a semiregular tiling of the Euclidean plane. There is one square and two octagons on each vertex
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
. This is the only edge-to-edge tiling by regular convex polygons which contains an octagon. It has Schläfli symbol of t0,1{4,4}.
Conway
John Horton Conway
John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...
calls it a truncated quadrille, constructed as a truncation
Truncation (geometry)
In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :...
operation applied to a square tiling (quadrille).
Other names used for this pattern include Mediterranean tiling and octagonal tiling.
There are 3 regular and 8 semiregular tilings in the plane.
Uniform colorings
There are two distinct uniform coloringUniform coloring
In geometry, a uniform coloring is a property of a uniform figure that is colored to be vertex-transitive...
s of a truncated square tiling. (Naming the colors by indices around a vertex (4.8.8): 122, 123.)
 2 colors: 122 |
 3 colors: 123 |
Related polyhedra and tilings
It is topologicallyTopology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
related to the polyhedron truncated octahedron
Truncated octahedron
In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron....
, 4.6.6.

The Pythagorean tiling
Pythagorean tiling
In geometry, the Pythagorean tiling or two squares tessellation is a tessellation of the plane by squares of two different sizes, in which each square touches four squares of the other size on its four sides. A tiling of this type may be formed by squares of any two different sizes...
alternates large and small squares, and may be seen as topologically identical to the truncated square tiling. The squares are rotated 45 degrees and octagons are distorted into squares with mid-edge vertices.
 |
 |
 |
| This tiling (with two chiral Chirality (mathematics) In geometry, a figure is chiral if it is not identical to its mirror image, or, more precisely, if it cannot be mapped to its mirror image by rotations and translations alone. For example, a right shoe is different from a left shoe, and clockwise is different from counterclockwise.A chiral object... forms and two uniform coloring Uniform coloring In geometry, a uniform coloring is a property of a uniform figure that is colored to be vertex-transitive... s) sometimes is called the Pythagorean tiling because its geometry may be used in a proof for the Pythagorean theorem Pythagorean theorem In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle... . |
This weaving Weaving Weaving is a method of fabric production in which two distinct sets of yarns or threads are interlaced at right angles to form a fabric or cloth. The other methods are knitting, lace making and felting. The longitudinal threads are called the warp and the lateral threads are the weft or filling... pattern has the same topology as well, with octagons flattened into 3 by 1 rectangle Rectangle In Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle... s |
|

