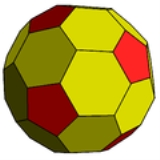
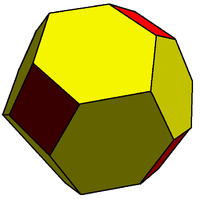
Truncated rhombic triacontahedron
Encyclopedia
| Truncated rhombic triacontahedron | |
|---|---|
 |
|
| Type | Conway polyhedron Conway polyhedron notation Conway polyhedron notation is used to describe polyhedra based on a seed polyhedron modified by various operations.The seed polyhedra are the Platonic solids, represented by their first letter of their name ; the prisms , antiprisms and pyramids... |
| Faces | 12 pentagon Pentagon In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and... s 30 hexagons |
| Edges | 120 (2 types) |
| Vertices | 80 (2 types) |
| Vertex configuration Vertex configuration In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron... |
(60) 5.6.6 (20) 6.6.6 |
| Symmetry group Symmetry group The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation... |
Icosahedral Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation... (Ih) |
| Dual polyhedron Dual polyhedron In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another... |
Pentakis icosidodecahedron Pentakis icosidodecahedron The pentakis icosidodecahedron is a convex polyhedron with 80 triangular faces, 120 edges, and 42 vertices. It a dual of the truncated rhombic triacontahedron.... |
| Properties | convex Convex set In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object... , equilateral Equilateral In geometry, an equilateral polygon is a polygon which has all sides of the same length.For instance, an equilateral triangle is a triangle of equal edge lengths... -faced |
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
polyhedron
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
constructed as a truncation
Truncation (geometry)
In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :...
of the rhombic triacontahedron
Rhombic triacontahedron
In geometry, the rhombic triacontahedron is a convex polyhedron with 30 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. It is the polyhedral dual of the icosidodecahedron, and it is a zonohedron....
. It can more accurately be called a pentatruncated rhombic triacontahedron because only the order-5 vertices are truncated.
These 12 order-5 vertices can be truncated such that all edges are equal length. The original 30 rhombic
Rhombus
In Euclidean geometry, a rhombus or rhomb is a convex quadrilateral whose four sides all have the same length. The rhombus is often called a diamond, after the diamonds suit in playing cards, or a lozenge, though the latter sometimes refers specifically to a rhombus with a 45° angle.Every...
faces become non-regular hexagons, and the truncated vertices become regular pentagons.
The hexagon faces can be equilateral
Equilateral
In geometry, an equilateral polygon is a polygon which has all sides of the same length.For instance, an equilateral triangle is a triangle of equal edge lengths...
but not regular
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
with D2 symmetry. The angles at the two vertices with vertex configuration
Vertex configuration
In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron...
6.6.6 are arccos(-1/sqrt(5)) = 116.565 degrees, and at the remaining four vertices with 5.6.6, they are 121.717 degrees each.
Full truncation
If all 32 vertices of a rhombic triacontahedron are truncated, the resulting solid has 12 regular pentagons, 20 equilateral triangles and 30 irregular octagons, with 180 edges in all, and 120 vertices. Its dual is a triangular hecatonicosahedron known as the tripentakis icosidodecahedron, a solid formed by adding a low pyramid to each face of a uniform icosidodecahedronIcosidodecahedron
In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon...
. This figure is to the dodecahedron as the truncated cube
Truncated cube
In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices....
is to the tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
.
Related polyhedra and polytopes
This polyhedron looks very similar to the uniform truncated icosahedronTruncated icosahedron
In geometry, the truncated icosahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids whose faces are two or more types of regular polygons.It has 12 regular pentagonal faces, 20 regular hexagonal faces, 60 vertices and 90 edges....
which has 12 pentagons, but only 20 hexagons.
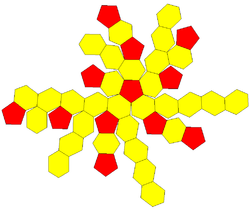
It also represents the exterior envelope of a cell-centered orthogonal projection of the 120-cell, one of six (convex regular 4-polytopes).
This polyhedron is also a part of a sequence of truncated rhombic polyhedra and tilings with [n,3] Coxeter group
Coxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
symmetry. The cube can be seen as a rhombic hexahedron where the rhombi are squares. The truncated forms have regular n-gons at the truncated vertices, and nonregular hexagonal faces. The sequence has two vertex figures (n.6.6) and (6,6,6).
| Polyhedra | Euclidean tiling | Hyperbolic tiling | |||
|---|---|---|---|---|---|
| [3,3] | [4,3] | [5,3] | [6,3] | [7,3] | [8,3] |
 Cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
 Rhombic dodecahedron Rhombic dodecahedron In geometry, the rhombic dodecahedron is a convex polyhedron with 12 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. Its dual is the cuboctahedron.-Properties:... |
 Rhombic triacontahedron Rhombic triacontahedron In geometry, the rhombic triacontahedron is a convex polyhedron with 30 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. It is the polyhedral dual of the icosidodecahedron, and it is a zonohedron.... |
Rhombille |
 |
|
 Alternate truncated cube |
 Truncated rhombic dodecahedron Truncated rhombic dodecahedron The truncated rhombic dodecahedron is a convex polyhedron constructed from the rhombic dodecahedron by truncating the 6 vertices.The 6 vertices are truncated such that all edges are equal length. The original 12 rhombic faces become flattened hexagons, and the truncated vertices become squares.The... |
 Truncated rhombic triacontahedron Truncated rhombic triacontahedron The truncated rhombic triacontahedron is a convex polyhedron constructed as a truncation of the rhombic triacontahedron. It can more accurately be called a pentatruncated rhombic triacontahedron because only the order-5 vertices are truncated.... |
Hexagonal tiling |
Chemistry
This is the shape of the fullereneFullerene
A fullerene is any molecule composed entirely of carbon, in the form of a hollow sphere, ellipsoid, or tube. Spherical fullerenes are also called buckyballs, and they resemble the balls used in association football. Cylindrical ones are called carbon nanotubes or buckytubes...
C80; sometimes this shape is denoted C80(Ih) to describe its icosahedral symmetry and distinguish it from other less-symmetric 80-vertex fullerenes. It is one of only four fullerenes found by to have a skeleton that can be isometrically embeddable into an L1 space
Taxicab geometry
Taxicab geometry, considered by Hermann Minkowski in the 19th century, is a form of geometry in which the usual distance function or metric of Euclidean geometry is replaced by a new metric in which the distance between two points is the sum of the absolute differences of their coordinates...
.
External links
- VTML polyhedral generator Try "t5daD" (Conway polyhedron notationConway polyhedron notationConway polyhedron notation is used to describe polyhedra based on a seed polyhedron modified by various operations.The seed polyhedra are the Platonic solids, represented by their first letter of their name ; the prisms , antiprisms and pyramids...
) - Zometool model
- Fullerene C80

