Rectification (geometry)
Encyclopedia

Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
, rectification is the process of truncating a polytope
Polytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
by marking the midpoints of all its edges, and cutting off its vertices at those points. The resulting polytope will be bounded by the vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
s and the rectified facets of the original polytope.
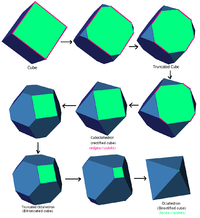
Example of rectification as a final truncation to an edge
Rectification is the final point of a truncation process. For example on a cube this sequence shows four steps of a continuum of truncations between the regular and rectified form:
Higher-order rectifications
Higher-order rectification can be performed on higher-dimensional regular polytopes. The highest order of rectification creates the dual polytope. A rectification truncates edges to points. A birectification truncates faces to points. A trirectification truncates cells to points. ... The final rectification is the dual polytope.Example of birectification as a final truncation to a face
This sequence shows a birectified cube as the final sequence from a cube to the dual where the original faces are truncated down to a single point:In polyhedra and plane tilings
Each platonic solidPlatonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
and its dual
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
have the same rectified polyhedron. (This is not true of polytopes in higher dimensions.)
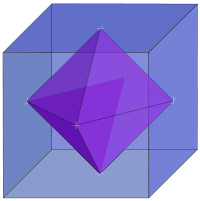
The rectified polyhedron turns out to be expressible as the intersection of the original platonic solid with an appropriated scaled concentric version of its dual. For this reason, its name is a combination of the names of the original and the dual:
- The rectified tetrahedronTetrahedronIn geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
, whose dual is the tetrahedron, is the tetratetrahedron, better known as the octahedronOctahedronIn geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
. - The rectified octahedronOctahedronIn geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
, whose dual is the cubeCubeIn geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
, is the cuboctahedronCuboctahedronIn geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...
. - The rectified icosahedronIcosahedronIn geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
, whose dual is the dodecahedron, is the icosidodecahedronIcosidodecahedronIn geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon...
. - A rectified square tiling is a square tiling.
- A rectified triangular tiling or hexagonal tiling is a trihexagonal tilingTrihexagonal tilingIn geometry, the trihexagonal tiling is a semiregular tiling of the Euclidean plane. There are two triangles and two hexagons alternating on each vertex...
.
Examples
| Family | Parent | Rectification | Dual |
|---|---|---|---|
| [3,3] |  Tetrahedron Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
 Tetratetrahedron Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
 Tetrahedron Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
| [4,3] |  Cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
 Cuboctahedron Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... |
 Octahedron Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
| [5,3] |  Dodecahedron |
 Icosidodecahedron Icosidodecahedron In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon... |
 Icosahedron Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... |
| [6,3] |  Hexagonal tiling |
 Trihexagonal tiling Trihexagonal tiling In geometry, the trihexagonal tiling is a semiregular tiling of the Euclidean plane. There are two triangles and two hexagons alternating on each vertex... |
 Triangular tiling |
| [7,3] |  Order-3 heptagonal tiling |
 Triheptagonal tiling Triheptagonal tiling In geometry, the triheptagonal tiling is a semiregular tiling of the hyperbolic plane, representing a rectified Order-3 heptagonal tiling. There are two triangles and two heptagons alternating on each vertex... |
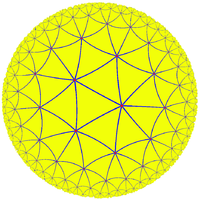 Order-7 triangular tiling |
| [4,4] |  Square tiling |
 Square tiling |
 Square tiling |
| [5,4] |  Order-4 pentagonal tiling |
 tetrapentagonal tiling |
 Order-5 square tiling |
In nonregular polyhedra
If a polyhedron is not regular, the edge midpoints surrounding a vertex may not be coplanar. However, a form of rectification is still possible in this case: every polyhedron has a polyhedral graphPolyhedral graph
In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the 3-vertex-connected planar graphs...
as its 1-skeleton
N-skeleton
In mathematics, particularly in algebraic topology, the n-skeleton of a topological space X presented as a simplicial complex refers to the subspace Xn that is the union of the simplices of X of dimensions m ≤ n...
, and from that graph one may form the medial graph by placing a vertex at each edge midpoint of the original graph, and connecting two of these new vertices by an edge whenever they belong to consecutive edges along a common face. The resulting medial graph remains polyhedral, so by Steinitz's theorem
Steinitz's theorem
In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the 3-vertex-connected planar graphs...
it can be represented as a polyhedron.
In polychora and 3d honeycomb tessellations
Each convex regular polychoronConvex regular 4-polytope
In mathematics, a convex regular 4-polytope is a 4-dimensional polytope that is both regular and convex. These are the four-dimensional analogs of the Platonic solids and the regular polygons ....
has a rectified form as a uniform polychoron
Uniform polychoron
In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
.
A regular polychoron {p,q,r} has cells {p,q}. Its rectification will have two cell types, a rectified {p,q} polyhedron left from the original cells and {q,r} polyhedron as new cells formed by each truncated vertex.
A rectified {p,q,r} is not the same as a rectified {r,q,p}, however. A further truncation, called bitruncation, is symmetric between a polychoron and its dual. See Uniform polychoron#Geometric derivations.
Examples
| Family | Parent | Rectification | Birectification (Dual rectification) |
Trirectification (Dual) |
|---|---|---|---|---|
| [3,3,3] |  5-cell |
 rectified 5-cell Rectified 5-cell In four dimensional geometry, the rectified 5-cell is a uniform polychoron composed of 5 regular tetrahedral and 5 regular octahedral cells. Each edge has one tetrahedron and two octahedra. Each vertex has two tetrahedra and three octahedra. In total it has 30 triangle faces, 30 edges, and 10... |
 rectified 5-cell Rectified 5-cell In four dimensional geometry, the rectified 5-cell is a uniform polychoron composed of 5 regular tetrahedral and 5 regular octahedral cells. Each edge has one tetrahedron and two octahedra. Each vertex has two tetrahedra and three octahedra. In total it has 30 triangle faces, 30 edges, and 10... |
 5-cell |
| [4,3,3] | 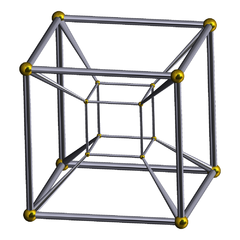 tesseract Tesseract In geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8... |
 rectified tesseract Rectified tesseract In geometry, the rectified tesseract, or rectified 8-cell is a uniform polychoron bounded by 24 cells: 8 cuboctahedra, and 16 tetrahedra.... |
 Rectified 16-cell (24-cell) |
 16-cell 16-cell In four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century.... |
| [3,4,3] | 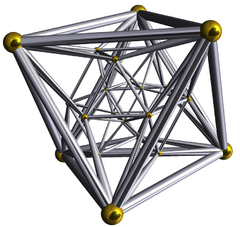 24-cell |
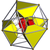 rectified 24-cell Rectified 24-cell In geometry, the rectified 24-cell is a uniform 4-dimensional polytope , which is bounded by 48 cells: 24 cubes, and 24 cuboctahedra. It can be obtained by reducing the icositetrachoron's cells to cubes or cuboctahedra.... |
 rectified 24-cell Rectified 24-cell In geometry, the rectified 24-cell is a uniform 4-dimensional polytope , which is bounded by 48 cells: 24 cubes, and 24 cuboctahedra. It can be obtained by reducing the icositetrachoron's cells to cubes or cuboctahedra.... |
 24-cell |
| [5,3,3] | 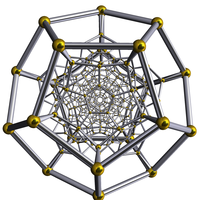 120-cell |
rectified 120-cell Rectified 120-cell In geometry, a rectified 120-cell is a uniform polychoron formed as the rectification of the regular 120-cell.There are four rectifications of the 120-cell, including the zeroth, the 120-cell itself... |
rectified 600-cell Rectified 600-cell In geometry, a rectified 600-cell is a uniform polychoron formed as the rectification of the regular 600-cell.There are four rectifications of the 600-cell, including the zeroth, the 600-cell itself... |
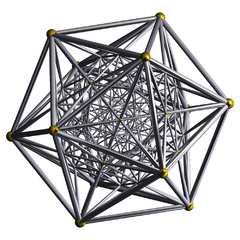 600-cell |
| [4,3,4] |  Cubic honeycomb Cubic honeycomb The cubic honeycomb is the only regular space-filling tessellation in Euclidean 3-space, made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron.... |
 Rectified cubic honeycomb Rectified cubic honeycomb The rectified cubic honeycomb is a uniform space-filling tessellation in Euclidean 3-space. It is composed of octahedra and cuboctahedra in a ratio of 1:1.- Symmetry :... |
 Rectified cubic honeycomb Rectified cubic honeycomb The rectified cubic honeycomb is a uniform space-filling tessellation in Euclidean 3-space. It is composed of octahedra and cuboctahedra in a ratio of 1:1.- Symmetry :... |
 Cubic honeycomb Cubic honeycomb The cubic honeycomb is the only regular space-filling tessellation in Euclidean 3-space, made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron.... |
| [5,3,4] |  Order-4 dodecahedral |
(No image) Rectified order-4 dodecahedral |
(No image) Rectified order-5 cubic |
 Order-5 cubic |
Orders of rectification
A first order rectification truncates edges down to points. If a polytope is regularRegular polytope
In mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of...
, this form is represented by an extended Schläfli symbol notation t1{p,q,...}.
A second order rectification, or birectification, truncates faces
Face (geometry)
In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...
down to points. If regular it has notation t2{p,q,...}. For polyhedra
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
, a birectification creates a dual polyhedron
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
.
Higher order rectifications can be constructed for higher order polytopes. In general an n-rectification truncates n-faces to points.
If an n-polytope is (n-1)-rectified, its facets
Facet (mathematics)
A facet of a simplicial complex is a maximal simplex.In the general theory of polyhedra and polytopes, two conflicting meanings are currently jostling for acceptability:...
are reduced to points and the polytope becomes its dual.
Notations and facets
There are different equivalent notations for each order of rectification. These tables show the names by dimension and the two type of facetFacet (mathematics)
A facet of a simplicial complex is a maximal simplex.In the general theory of polyhedra and polytopes, two conflicting meanings are currently jostling for acceptability:...
s for each.
Regular polygonPolygonIn geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
s
FacetFacet (mathematics)
A facet of a simplicial complex is a maximal simplex.In the general theory of polyhedra and polytopes, two conflicting meanings are currently jostling for acceptability:...
s are edges, represented as {2}.
| name {p} |
Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
t-notation Schläfli symbol |
Vertical Schläfli symbol | ||
|---|---|---|---|---|---|
| Name | Facet-1 | Facet-2 | |||
| Parent | t0{p} |  |
 |
||
| Rectified | t1{p} |  |
 |
Regular polyhedraUniform polyhedronA uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
and tilings
FacetFacet (mathematics)
A facet of a simplicial complex is a maximal simplex.In the general theory of polyhedra and polytopes, two conflicting meanings are currently jostling for acceptability:...
s are regular polygons.
| name {p,q} |
Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
t-notation Schläfli symbol |
Vertical Schläfli symbol | ||
|---|---|---|---|---|---|
| Name | Facet-1 | Facet-2 | |||
| Parent | t0{p,q} |  |
 |
||
| Rectified | t1{p,q} |  |
 |
 |
|
| Birectified | t2{p,q} |  |
 |
Regular polychoraUniform polychoronIn geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
and honeycombHoneycombA honeycomb is a mass of hexagonal waxcells built by honey bees in their nests to contain their larvae and stores of honey and pollen.Beekeepers may remove the entire honeycomb to harvest honey...
s
FacetFacet (mathematics)
A facet of a simplicial complex is a maximal simplex.In the general theory of polyhedra and polytopes, two conflicting meanings are currently jostling for acceptability:...
s are regular or rectified polyhedra.
| name {p,q,r} |
Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
t-notation Schläfli symbol |
Vertical Schläfli symbol | ||
|---|---|---|---|---|---|
| Name | Facet-1 | Facet-2 | |||
| Parent | t0{p,q,r} |  |
 |
||
| Rectified | t1{p,q,r} |  |
 |
 |
|
| Birectified | t2{p,q,r} |  |
 |
 |
|
| Trirectified | t3{p,q,r} |  |
 |
Regular polyterons and 4-space honeycombsHoneycomb (geometry)In geometry, a honeycomb is a space filling or close packing of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions....
FacetFacet (mathematics)
A facet of a simplicial complex is a maximal simplex.In the general theory of polyhedra and polytopes, two conflicting meanings are currently jostling for acceptability:...
s are regular or rectified polychora.
| name {p,q,r,s} |
Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
t-notation Schläfli symbol |
Vertical Schläfli symbol | ||
|---|---|---|---|---|---|
| Name | Facet-1 | Facet-2 | |||
| Parent | t0{p,q,r,s} |  |
 |
||
| Rectified | t1{p,q,r,s} |  |
 |
 |
|
| Birectified | t2{p,q,r,s} |  |
 |
 |
|
| Trirectified | t3{p,q,r,s} |  |
 |
 |
|
| Quadrirectified | t4{p,q,r,s} |  |
 |
See also
- Dual polytope
- Quasiregular polyhedronQuasiregular polyhedronIn geometry, a quasiregular polyhedron is a semiregular polyhedron that has exactly two kinds of regular faces, which alternate around each vertex. They are edge-transitive and hence step closer to regularity than the semiregular which are merely vertex-transitive.There are only two convex...
- List of regular polytopes
- Truncation (geometry)Truncation (geometry)In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :...
- Conway polyhedron notationConway polyhedron notationConway polyhedron notation is used to describe polyhedra based on a seed polyhedron modified by various operations.The seed polyhedra are the Platonic solids, represented by their first letter of their name ; the prisms , antiprisms and pyramids...