
Rydberg atom
Encyclopedia
A Rydberg atom is an excited atom
with one or more electron
s that have a very high principal quantum number
. These atom
s have a number of peculiar properties including an exaggerated response to electric
and magnetic field
s, long decay periods and electron
wavefunction
s that approximate, under some conditions, classical
orbits of electrons about the nuclei
. The core electrons shield the outer electron
from the electric field of the nucleus such that, from a distance, the electric potential
looks identical to that experienced by the electron in a hydrogen atom
.
In spite of its shortcomings, the Bohr model
of the atom is useful in explaining these properties. Classically an electron in a circular orbit of radius r, about a nucleus
of charge +e
, obeys Newton's second law
:

where k = 1/(4πε0).
Orbital momentum is quantized
in units of ħ:
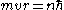 .
.
Combining these two equations leads to Bohr
's expression for the orbital radius in terms of the principal quantum number
, n:
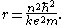
It is now apparent why Rydberg atoms have such peculiar properties: the radius of the orbit scales as n2 (the n = 137 state of hydrogen has an atomic radius ~1 µm) and the geometric cross-section as n4. Thus Rydberg atoms are extremely large with loosely bound valence electrons, easily perturbed or ionized
by collisions or external fields.
Because the binding energy
of a Rydberg electron is proportional to 1/r and hence falls off like 1/n2, the energy level spacing falls off like 1/n3 leading to ever more closely spaced levels converging on the first ionization energy
. These closely spaced Rydberg states form what is commonly referred to as the Rydberg series. Figure 1 shows some of the energy levels of the lowest three values of orbital angular momentum
in lithium
.
s of light associated with transitions in atomic hydrogen
. Three years later the Swedish physicist Johannes Rydberg
presented a generalized and more intuitive version of Balmer's formula that came to be known as the Rydberg formula
. This formula indicated the existence of an infinite series of ever more closely spaced discrete energy level
s converging on a finite limit.
This series was qualitatively explained in 1913 by Niels Bohr
with his semiclassical model
of the hydrogen atom in which quantized
values of angular momentum lead to the observed discrete energy levels. A full quantitative derivation of the observed spectrum was derived by Wolfgang Pauli
in 1926 following development of quantum mechanics
by Werner Heisenberg
and others.
processes can use the electron kinetic energy
to increase the atoms' internal energy exciting to a broad range of different states including many high-lying Rydberg states,
 .
.
Because the electron can retain any arbitrary amount of its initial kinetic energy this process always results in a population with a broad spread of different energies.
s and a population of neutral atoms of another species resulting in the formation of a beam of highly excited atoms,
 .
.
Again, because the kinetic energy of the interaction can contribute to the final internal energies of the constituents this technique populates a broad range of energy levels.
s in the 1970s allowed a much greater level of control over populations of excited atoms. In optical excitation the incident photon
is absorbed by the target atom, absolutely specifying the final state energy. The problem of producing single state, mono-energetic populations of Rydberg atoms thus becomes the somewhat simpler problem of precisely controlling the frequency of the laser output,
 .
.
This form of direct optical excitation is generally limited to experiments with the alkali metal
s because the ground state binding energy
in other species is generally too high to be accessible with most laser systems.
For atoms with a large valence electron
binding energy
(equivalent to a large first ionization energy
) the excited states of the Rydberg series are inaccessible with conventional laser systems. Initial collisional excitation can make up the energy shortfall allowing optical excitation to be used to select the final state. Although the initial step excites to a broad range of intermediate states, the precision inherent in the optical excitation process means that the laser light only interacts with a specific subset of atoms in a particular state, exciting to the chosen final state.
 An atom in a Rydberg state
An atom in a Rydberg state
has a valence electron in a large orbit far from the ion core; in such an orbit the outermost electron feels an almost hydrogenic
, Coulomb potential
, UC from a compact ion core consisting of a nucleus
with Z
proton
s and the lower electron shells filled with Z-1 electrons. An electron in the spherically symmetric Coulomb potential has potential energy:
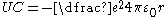 .
.
The similarity of the effective potential ‘seen’ by the outer electron to the hydrogen potential is a defining characteristic of Rydberg states
and explains why the electron wavefunctions approximate to classical orbits in the limit of the correspondence principle
. In other words, the electron's orbit resembles the orbit of planets inside a solar system, much like the obsolete but visually useful Bohr
and Rutherford
models of the atom used to show.
There are three notable exceptions that can be characterized by the additional term added to the potential energy:
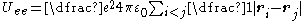 .
.
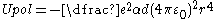 ,
,
 Quantum mechanically a state with abnormally high n refers to an atom in which the valence electron(s) have been excited into a formerly unpopulated electron orbital
Quantum mechanically a state with abnormally high n refers to an atom in which the valence electron(s) have been excited into a formerly unpopulated electron orbital
with higher energy and lower binding energy
. In hydrogen the binding energy is given by:
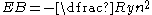 ,
,
where Ry = 13.6 eV is the Rydberg constant
. The low binding energy at high values of n explains why Rydberg states are susceptible to ionization.
Additional terms in the potential energy expression for a Rydberg state, on top of the hydrogenic Coulomb potential energy require the introduction of a quantum defect
, δl, into the expression for the binding energy:
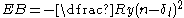 .
.
The three exceptions to the definition of a Rydberg atom as an atom with a hydrogenic potential, have an alternative, quantum mechanical description that can be characterized by the additional term(s) in the atomic Hamiltonian
:
, d. There is an energy associated with the presence of an electric dipole in an electric field
, F, known in atomic physics as a Stark shift
,

Depending on the sign of the projection of the dipole moment onto the local electric field vector a state may have energy that increases or decreases with field strength (low-field and high-field seeking states respectively). The narrow spacing between adjacent n-levels in the Rydberg series means that states can approach degeneracy
even for relatively modest field strengths. The theoretical field strength at which a crossing would occur assuming no coupling between the states is given by the Inglis-Teller limit
,
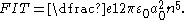
In the hydrogen atom
, the pure 1/r Coulomb potential does not couple Stark states from adjacent n-manifolds resulting in real crossings as shown in figure 4. The presence of additional terms in the potential energy can lead to coupling resulting in avoided crossings as shown for lithium
in figure 5.
, Χ. As diamagnetic effects scale with the area of the orbit and the area is proportional to the radius squared (A ∝ n4), effects impossible to detect in ground state atoms become obvious in Rydberg atoms, which demonstrate very large diamagnetic shifts.
s due to the recombination of electrons and positive ions; low energy recombination results in fairly stable Rydberg atoms, while recombination of electrons and positive ions with high kinetic energy
often form autoionising
Rydberg states. Rydberg atoms’ large sizes and susceptibility to perturbation and ionisation by electric and magnetic fields, are an important factor determining the properties of plasmas.
Condensation of Rydberg atoms forms Rydberg matter
most often observed in form of long-lived clusters. The de-excitation is significantly impeded in Rydberg matter by exchange-correlation effects in the non-uniform electron liquid formed on condensation by the collective valence electrons, which causes extended lifetime of clusters.
experiments and the arrival of tunable lasers, interest in Rydberg atoms was kept alive by the realisation that they are common in interstellar space, and as such are an important radiation source for astronomers.
The density within interstellar gas clouds is typically many orders of magnitude lower than the best laboratory vacuums attainable on Earth, allowing Rydberg atoms to persist for long periods of time without being ionised by collisions or electric and magnetic fields. As a result of this longevity and the abundance of hydrogen it is particularly common for astronomers to observe radiation from the heavens at a frequency of 2.4 GHz, now known to correspond to the hydrogen n = 109 to n = 108 transition. Such a highly excited hydrogen atom on Earth would be ionised almost immediately as the binding energy
would be significantly below thermal energies
.
s. Calculations using perturbation theory
show that this results in strong interactions between two close Rydberg atoms. Coherent control of these interactions combined with the their relatively long lifetime makes them a suitable candidate to realize a quantum computer
. , a two-qubit
gate
has not been achieved experimentally; however, observations of collective excitations or conditional dynamics have been reported, both between two individual atoms and in mesoscopic samples. Strongly interacting Rydberg atoms also feature quantum critical
behavior, which makes them interesting to study on their own.

 A simple 1/r potential results in a closed Keplerian elliptical orbit
A simple 1/r potential results in a closed Keplerian elliptical orbit
. In the presence of an external electric field
Rydberg atoms can obtain very large electric dipole moment
s making them extremely susceptible to perturbation by the field. Figure 6 shows how application of an external electric field (known in atomic physics as a Stark
field) changes the geometry of the potential, dramatically changing the behaviour of the electron. A Coulombic potential does not apply any torque
as the force is always antiparallel
to the position vector (always pointing along a line running between the electron and the nucleus):
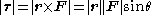 ,
,
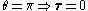 .
.
With the application of a static electric field, the electron feels a continuously changing torque. The resulting trajectory becomes progressively more distorted over time, eventually going through the full range of angular momentum from L = LMAX, to a straight line L=0, to the initial orbit in the opposite sense
L = -LMAX.
The time period of the oscillation in angular momentum (the time to complete the trajectory in figure 7), almost exactly matches the quantum mechanically predicted period for the wavefunction to return to its initial state, demonstrating the classical nature of the Rydberg atom.
Excited state
Excitation is an elevation in energy level above an arbitrary baseline energy state. In physics there is a specific technical definition for energy level which is often associated with an atom being excited to an excited state....
with one or more electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
s that have a very high principal quantum number
Principal quantum number
In atomic physics, the principal quantum symbolized as n is the firstof a set of quantum numbers of an atomic orbital. The principal quantum number can only have positive integer values...
. These atom
Atom
The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...
s have a number of peculiar properties including an exaggerated response to electric
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
and magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
s, long decay periods and electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
wavefunction
Wavefunction
Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
s that approximate, under some conditions, classical
Classical physics
What "classical physics" refers to depends on the context. When discussing special relativity, it refers to the Newtonian physics which preceded relativity, i.e. the branches of physics based on principles developed before the rise of relativity and quantum mechanics...
orbits of electrons about the nuclei
Atomic nucleus
The nucleus is the very dense region consisting of protons and neutrons at the center of an atom. It was discovered in 1911, as a result of Ernest Rutherford's interpretation of the famous 1909 Rutherford experiment performed by Hans Geiger and Ernest Marsden, under the direction of Rutherford. The...
. The core electrons shield the outer electron
Valence electron
In chemistry, valence electrons are the electrons of an atom that can participate in the formation of chemical bonds with other atoms. Valence electrons are the "own" electrons, present in the free neutral atom, that combine with valence electrons of other atoms to form chemical bonds. In a single...
from the electric field of the nucleus such that, from a distance, the electric potential
Electric potential
In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
looks identical to that experienced by the electron in a hydrogen atom
Hydrogen atom
A hydrogen atom is an atom of the chemical element hydrogen. The electrically neutral atom contains a single positively-charged proton and a single negatively-charged electron bound to the nucleus by the Coulomb force...
.
In spite of its shortcomings, the Bohr model
Bohr model
In atomic physics, the Bohr model, introduced by Niels Bohr in 1913, depicts the atom as a small, positively charged nucleus surrounded by electrons that travel in circular orbits around the nucleus—similar in structure to the solar system, but with electrostatic forces providing attraction,...
of the atom is useful in explaining these properties. Classically an electron in a circular orbit of radius r, about a nucleus
Atomic nucleus
The nucleus is the very dense region consisting of protons and neutrons at the center of an atom. It was discovered in 1911, as a result of Ernest Rutherford's interpretation of the famous 1909 Rutherford experiment performed by Hans Geiger and Ernest Marsden, under the direction of Rutherford. The...
of charge +e
Elementary charge
The elementary charge, usually denoted as e, is the electric charge carried by a single proton, or equivalently, the absolute value of the electric charge carried by a single electron. This elementary charge is a fundamental physical constant. To avoid confusion over its sign, e is sometimes called...
, obeys Newton's second law
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
:

where k = 1/(4πε0).
Orbital momentum is quantized
Quantization (physics)
In physics, quantization is the process of explaining a classical understanding of physical phenomena in terms of a newer understanding known as "quantum mechanics". It is a procedure for constructing a quantum field theory starting from a classical field theory. This is a generalization of the...
in units of ħ:
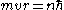 .
.Combining these two equations leads to Bohr
Niels Bohr
Niels Henrik David Bohr was a Danish physicist who made foundational contributions to understanding atomic structure and quantum mechanics, for which he received the Nobel Prize in Physics in 1922. Bohr mentored and collaborated with many of the top physicists of the century at his institute in...
's expression for the orbital radius in terms of the principal quantum number
Principal quantum number
In atomic physics, the principal quantum symbolized as n is the firstof a set of quantum numbers of an atomic orbital. The principal quantum number can only have positive integer values...
, n:
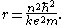
It is now apparent why Rydberg atoms have such peculiar properties: the radius of the orbit scales as n2 (the n = 137 state of hydrogen has an atomic radius ~1 µm) and the geometric cross-section as n4. Thus Rydberg atoms are extremely large with loosely bound valence electrons, easily perturbed or ionized
Ionization potential
The ionization energy of a chemical species, i.e. an atom or molecule, is the energy required to remove an electron from the species to a practically infinite distance. Large atoms or molecules have a low ionization energy, while small molecules tend to have higher ionization energies.The property...
by collisions or external fields.
Because the binding energy
Binding energy
Binding energy is the mechanical energy required to disassemble a whole into separate parts. A bound system typically has a lower potential energy than its constituent parts; this is what keeps the system together—often this means that energy is released upon the creation of a bound state...
of a Rydberg electron is proportional to 1/r and hence falls off like 1/n2, the energy level spacing falls off like 1/n3 leading to ever more closely spaced levels converging on the first ionization energy
Ionization energy
The ionization energy of a chemical species, i.e. an atom or molecule, is the energy required to remove an electron from the species to a practically infinite distance. Large atoms or molecules have a low ionization energy, while small molecules tend to have higher ionization energies.The property...
. These closely spaced Rydberg states form what is commonly referred to as the Rydberg series. Figure 1 shows some of the energy levels of the lowest three values of orbital angular momentum
Azimuthal quantum number
The azimuthal quantum number is a quantum number for an atomic orbital that determines its orbital angular momentum and describes the shape of the orbital...
in lithium
Lithium
Lithium is a soft, silver-white metal that belongs to the alkali metal group of chemical elements. It is represented by the symbol Li, and it has the atomic number 3. Under standard conditions it is the lightest metal and the least dense solid element. Like all alkali metals, lithium is highly...
.
History
The existence of the Rydberg series was first demonstrated in 1885 when Johann Balmer discovered a simple empirical formula for the wavelengthWavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
s of light associated with transitions in atomic hydrogen
Hydrogen
Hydrogen is the chemical element with atomic number 1. It is represented by the symbol H. With an average atomic weight of , hydrogen is the lightest and most abundant chemical element, constituting roughly 75% of the Universe's chemical elemental mass. Stars in the main sequence are mainly...
. Three years later the Swedish physicist Johannes Rydberg
Johannes Rydberg
Johannes Robert Rydberg, , , was a Swedish physicist mainly known for devising the Rydberg formula, in 1888, which is used to predict the wavelengths of photons emitted by changes in the energy level of an electron in a hydrogen atom.The physical constant known as the...
presented a generalized and more intuitive version of Balmer's formula that came to be known as the Rydberg formula
Rydberg formula
The Rydberg formula is used in atomic physics to describe the wavelengths of spectral lines of many chemical elements. It was formulated by the Swedish physicist Johannes Rydberg, and presented on November 5, 1888.-History:...
. This formula indicated the existence of an infinite series of ever more closely spaced discrete energy level
Energy level
A quantum mechanical system or particle that is bound -- that is, confined spatially—can only take on certain discrete values of energy. This contrasts with classical particles, which can have any energy. These discrete values are called energy levels...
s converging on a finite limit.
This series was qualitatively explained in 1913 by Niels Bohr
Niels Bohr
Niels Henrik David Bohr was a Danish physicist who made foundational contributions to understanding atomic structure and quantum mechanics, for which he received the Nobel Prize in Physics in 1922. Bohr mentored and collaborated with many of the top physicists of the century at his institute in...
with his semiclassical model
Bohr model
In atomic physics, the Bohr model, introduced by Niels Bohr in 1913, depicts the atom as a small, positively charged nucleus surrounded by electrons that travel in circular orbits around the nucleus—similar in structure to the solar system, but with electrostatic forces providing attraction,...
of the hydrogen atom in which quantized
Quantization (physics)
In physics, quantization is the process of explaining a classical understanding of physical phenomena in terms of a newer understanding known as "quantum mechanics". It is a procedure for constructing a quantum field theory starting from a classical field theory. This is a generalization of the...
values of angular momentum lead to the observed discrete energy levels. A full quantitative derivation of the observed spectrum was derived by Wolfgang Pauli
Wolfgang Pauli
Wolfgang Ernst Pauli was an Austrian theoretical physicist and one of the pioneers of quantum physics. In 1945, after being nominated by Albert Einstein, he received the Nobel Prize in Physics for his "decisive contribution through his discovery of a new law of Nature, the exclusion principle or...
in 1926 following development of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
by Werner Heisenberg
Werner Heisenberg
Werner Karl Heisenberg was a German theoretical physicist who made foundational contributions to quantum mechanics and is best known for asserting the uncertainty principle of quantum theory...
and others.
Methods of production
The only truly stable state of an atom is the ground state with n = 1. The study of Rydberg states requires a reliable technique for exciting ground state atoms to states with a large value of n.Electron impact excitation
Much early experimental work on Rydberg atoms relied on the use of collimated beams of fast electrons incident on ground-state atoms. Inelastic scatteringInelastic scattering
In particle physics and chemistry, inelastic scattering is a fundamental scattering process in which the kinetic energy of an incident particle is not conserved . In an inelastic scattering process, some of the energy of the incident particle is lost or gained...
processes can use the electron kinetic energy
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
to increase the atoms' internal energy exciting to a broad range of different states including many high-lying Rydberg states,
 .
.Because the electron can retain any arbitrary amount of its initial kinetic energy this process always results in a population with a broad spread of different energies.
Charge exchange excitation
Another mainstay of early Rydberg atom experiments relied in charge exchange between a beam of ionIon
An ion is an atom or molecule in which the total number of electrons is not equal to the total number of protons, giving it a net positive or negative electrical charge. The name was given by physicist Michael Faraday for the substances that allow a current to pass between electrodes in a...
s and a population of neutral atoms of another species resulting in the formation of a beam of highly excited atoms,
 .
.Again, because the kinetic energy of the interaction can contribute to the final internal energies of the constituents this technique populates a broad range of energy levels.
Optical excitation
The arrival of tunable dye laserDye laser
A dye laser is a laser which uses an organic dye as the lasing medium, usually as a liquid solution. Compared to gases and most solid state lasing media, a dye can usually be used for a much wider range of wavelengths. The wide bandwidth makes them particularly suitable for tunable lasers and...
s in the 1970s allowed a much greater level of control over populations of excited atoms. In optical excitation the incident photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
is absorbed by the target atom, absolutely specifying the final state energy. The problem of producing single state, mono-energetic populations of Rydberg atoms thus becomes the somewhat simpler problem of precisely controlling the frequency of the laser output,
 .
.This form of direct optical excitation is generally limited to experiments with the alkali metal
Alkali metal
The alkali metals are a series of chemical elements in the periodic table. In the modern IUPAC nomenclature, the alkali metals comprise the group 1 elements, along with hydrogen. The alkali metals are lithium , sodium , potassium , rubidium , caesium , and francium...
s because the ground state binding energy
Binding energy
Binding energy is the mechanical energy required to disassemble a whole into separate parts. A bound system typically has a lower potential energy than its constituent parts; this is what keeps the system together—often this means that energy is released upon the creation of a bound state...
in other species is generally too high to be accessible with most laser systems.
For atoms with a large valence electron
Valence electron
In chemistry, valence electrons are the electrons of an atom that can participate in the formation of chemical bonds with other atoms. Valence electrons are the "own" electrons, present in the free neutral atom, that combine with valence electrons of other atoms to form chemical bonds. In a single...
binding energy
Binding energy
Binding energy is the mechanical energy required to disassemble a whole into separate parts. A bound system typically has a lower potential energy than its constituent parts; this is what keeps the system together—often this means that energy is released upon the creation of a bound state...
(equivalent to a large first ionization energy
Ionization energy
The ionization energy of a chemical species, i.e. an atom or molecule, is the energy required to remove an electron from the species to a practically infinite distance. Large atoms or molecules have a low ionization energy, while small molecules tend to have higher ionization energies.The property...
) the excited states of the Rydberg series are inaccessible with conventional laser systems. Initial collisional excitation can make up the energy shortfall allowing optical excitation to be used to select the final state. Although the initial step excites to a broad range of intermediate states, the precision inherent in the optical excitation process means that the laser light only interacts with a specific subset of atoms in a particular state, exciting to the chosen final state.
Hydrogenic potential

Rydberg states
The Rydberg states of an atom are electronically excited states with energies that follow the Rydberg formula as they converge on an ionic state with an ionization energy. Although the Rydberg formula was developed to describe atomic energy levels, it has been used to describe many other systems...
has a valence electron in a large orbit far from the ion core; in such an orbit the outermost electron feels an almost hydrogenic
Hydrogen-like atom
A hydrogen-like ion is any atomic nucleus with one electron and thus is isoelectronic with hydrogen. Except for the hydrogen atom itself , these ions carry the positive charge e, where Z is the atomic number of the atom. Examples of hydrogen-like ions are He+, Li2+, Be3+ and B4+...
, Coulomb potential
Potential well
A potential well is the region surrounding a local minimum of potential energy. Energy captured in a potential well is unable to convert to another type of energy because it is captured in the local minimum of a potential well...
, UC from a compact ion core consisting of a nucleus
Atomic nucleus
The nucleus is the very dense region consisting of protons and neutrons at the center of an atom. It was discovered in 1911, as a result of Ernest Rutherford's interpretation of the famous 1909 Rutherford experiment performed by Hans Geiger and Ernest Marsden, under the direction of Rutherford. The...
with Z
Atomic number
In chemistry and physics, the atomic number is the number of protons found in the nucleus of an atom and therefore identical to the charge number of the nucleus. It is conventionally represented by the symbol Z. The atomic number uniquely identifies a chemical element...
proton
Proton
The proton is a subatomic particle with the symbol or and a positive electric charge of 1 elementary charge. One or more protons are present in the nucleus of each atom, along with neutrons. The number of protons in each atom is its atomic number....
s and the lower electron shells filled with Z-1 electrons. An electron in the spherically symmetric Coulomb potential has potential energy:
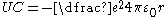 .
.The similarity of the effective potential ‘seen’ by the outer electron to the hydrogen potential is a defining characteristic of Rydberg states
Rydberg states
The Rydberg states of an atom are electronically excited states with energies that follow the Rydberg formula as they converge on an ionic state with an ionization energy. Although the Rydberg formula was developed to describe atomic energy levels, it has been used to describe many other systems...
and explains why the electron wavefunctions approximate to classical orbits in the limit of the correspondence principle
Correspondence principle
In physics, the correspondence principle states that the behavior of systems described by the theory of quantum mechanics reproduces classical physics in the limit of large quantum numbers....
. In other words, the electron's orbit resembles the orbit of planets inside a solar system, much like the obsolete but visually useful Bohr
Bohr model
In atomic physics, the Bohr model, introduced by Niels Bohr in 1913, depicts the atom as a small, positively charged nucleus surrounded by electrons that travel in circular orbits around the nucleus—similar in structure to the solar system, but with electrostatic forces providing attraction,...
and Rutherford
Rutherford model
The Rutherford model or planetary model is a model of the atom devised by Ernest Rutherford. Rutherford directed the famous Geiger-Marsden experiment in 1909, which suggested on Rutherford's 1911 analysis that the so-called "plum pudding model" of J. J. Thomson of the atom was incorrect...
models of the atom used to show.
There are three notable exceptions that can be characterized by the additional term added to the potential energy:
- An atom may have two (or more) electrons in highly excited states with comparable orbital radii. In this case the electron-electron interaction gives rise to a significant deviation from the hydrogen potential. For an atom in a multiple Rydberg state, the additional term, Uee, includes a summation of each pair of highly excited electrons:
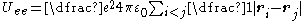 .
.- If the valence electron has very low angular momentum (interpreted classically as an extremely eccentricEccentricity (mathematics)In mathematics, the eccentricity, denoted e or \varepsilon, is a parameter associated with every conic section. It can be thought of as a measure of how much the conic section deviates from being circular.In particular,...
elliptical orbit) then it may pass close enough to polarise the ion core, giving rise to a 1/r4 core polarization term in the potential. The interaction between an inducedPolarizabilityPolarizability is the measure of the change in a molecule's electron distribution in response to an applied electric field, which can also be induced by electric interactions with solvents or ionic reagents. It is a property of matter...
dipoleElectric dipole momentIn physics, the electric dipole moment is a measure of the separation of positive and negative electrical charges in a system of charges, that is, a measure of the charge system's overall polarity with SI units of Coulomb-meter...
and the charge that produces it is always attractive so this contribution is always negative,
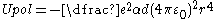 ,
,- where αd is the dipole polarizabilityPolarizabilityPolarizability is the measure of the change in a molecule's electron distribution in response to an applied electric field, which can also be induced by electric interactions with solvents or ionic reagents. It is a property of matter...
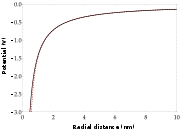
. Figure 2 shows how the polarization term modifies the potential close to the nucleus.
- If the outer electron penetrates the inner electron shells, it will 'see' more of the charge of the nucleus and hence experience a greater force. In general the modification to the potential energy is not simple to calculate and must be based on knowledge of the geometry of the ion core.
Quantum-mechanical details

Atomic orbital
An atomic orbital is a mathematical function that describes the wave-like behavior of either one electron or a pair of electrons in an atom. This function can be used to calculate the probability of finding any electron of an atom in any specific region around the atom's nucleus...
with higher energy and lower binding energy
Binding energy
Binding energy is the mechanical energy required to disassemble a whole into separate parts. A bound system typically has a lower potential energy than its constituent parts; this is what keeps the system together—often this means that energy is released upon the creation of a bound state...
. In hydrogen the binding energy is given by:
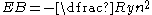 ,
,where Ry = 13.6 eV is the Rydberg constant
Rydberg constant
The Rydberg constant, symbol R∞, named after the Swedish physicist Johannes Rydberg, is a physical constant relating to atomic spectra in the science of spectroscopy. Rydberg initially determined its value empirically from spectroscopy, but Niels Bohr later showed that its value could be calculated...
. The low binding energy at high values of n explains why Rydberg states are susceptible to ionization.
Additional terms in the potential energy expression for a Rydberg state, on top of the hydrogenic Coulomb potential energy require the introduction of a quantum defect
Quantum defect
The term quantum defect is ambiguous. Various meanings are discussed below. Characteristic is that the defect deals with the loss on the smallest energy scale of light: that of the quantum.-Quantum defect in laser science:...
, δl, into the expression for the binding energy:
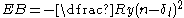 .
.Electron wavefunctions
The long lifetimes of Rydberg states with high orbital angular momentum can be explained in terms of the overlapping of wavefunctions. The wavefunction of an electron in a high l state (high angular momentum, 'circular orbit') has very little overlap with the wavefunctions of the inner electrons and hence remains relatively unperturbed.The three exceptions to the definition of a Rydberg atom as an atom with a hydrogenic potential, have an alternative, quantum mechanical description that can be characterized by the additional term(s) in the atomic Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
:
- If a second electron is excited into a state ni, energetically close to the state of the outer electron no, then its wavefunction become almost as large as the first (a double Rydberg state). This occurs as ni approaches no and leads to a condition where the size of the two electron’s orbits are related; a condition sometimes referred to as radial correlation. An electron-electron repulsion term must be included in the atomic Hamiltonian.
- Polarization of the ion core produces an anisotropicAnisotropyAnisotropy is the property of being directionally dependent, as opposed to isotropy, which implies identical properties in all directions. It can be defined as a difference, when measured along different axes, in a material's physical or mechanical properties An example of anisotropy is the light...
potential that causes an angular correlation between the motions of the two outermost electrons. This can be thought of as a tidal lockingTidal lockingTidal locking occurs when the gravitational gradient makes one side of an astronomical body always face another; for example, the same side of the Earth's Moon always faces the Earth. A tidally locked body takes just as long to rotate around its own axis as it does to revolve around its partner...
effect due to a non-spherically symmetric potential. A core polarization term must be included in the atomic Hamiltonian. - The wavefunction of the outer electron in states with low orbital angular momentum l, is periodically localised within the shells of inner electrons and interacts with the full charge of the nucleus. Figure 3 shows a semi-classicalOld quantum theoryThe old quantum theory was a collection of results from the years 1900–1925 which predate modern quantum mechanics. The theory was never complete or self-consistent, but was a collection of heuristic prescriptions which are now understood to be the first quantum corrections to classical mechanics...
interpretation of angular momentum states in an electron orbital, illustrating that low-l states pass closer to the nucleus potentially penetrating the ion core. A core penetration term must be added to the atomic Hamiltonian.
Rydberg atoms in external fields
The large separation between the electron and ion-core in a Rydberg atom makes possible an extremely large electric dipole momentElectric dipole moment
In physics, the electric dipole moment is a measure of the separation of positive and negative electrical charges in a system of charges, that is, a measure of the charge system's overall polarity with SI units of Coulomb-meter...
, d. There is an energy associated with the presence of an electric dipole in an electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
, F, known in atomic physics as a Stark shift
Stark effect
The Stark effect is the shifting and splitting of spectral lines of atoms and molecules due to presence of an external static electric field. The amount of splitting and or shifting is called the Stark splitting or Stark shift. In general one distinguishes first- and second-order Stark effects...
,

Depending on the sign of the projection of the dipole moment onto the local electric field vector a state may have energy that increases or decreases with field strength (low-field and high-field seeking states respectively). The narrow spacing between adjacent n-levels in the Rydberg series means that states can approach degeneracy
Degenerate energy level
In physics, two or more different quantum states are said to be degenerate if they are all at the same energy level. Statistically this means that they are all equally probable of being filled, and in Quantum Mechanics it is represented mathematically by the Hamiltonian for the system having more...
even for relatively modest field strengths. The theoretical field strength at which a crossing would occur assuming no coupling between the states is given by the Inglis-Teller limit
Inglis-Teller equation
The Inglis–Teller equation represents an approximate relationship between an energy level and the electron number density. This equation is related to the Stark effect in which spectral lines are split explicitly due to the presence of an electric field. The equation was derived by David R...
,
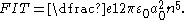
In the hydrogen atom
Hydrogen atom
A hydrogen atom is an atom of the chemical element hydrogen. The electrically neutral atom contains a single positively-charged proton and a single negatively-charged electron bound to the nucleus by the Coulomb force...
, the pure 1/r Coulomb potential does not couple Stark states from adjacent n-manifolds resulting in real crossings as shown in figure 4. The presence of additional terms in the potential energy can lead to coupling resulting in avoided crossings as shown for lithium
Lithium
Lithium is a soft, silver-white metal that belongs to the alkali metal group of chemical elements. It is represented by the symbol Li, and it has the atomic number 3. Under standard conditions it is the lightest metal and the least dense solid element. Like all alkali metals, lithium is highly...
in figure 5.
Investigating diamagnetic effects
The large sizes and low binding energies of Rydberg atoms lead to a high magnetic susceptibilityMagnetic susceptibility
In electromagnetism, the magnetic susceptibility \chi_m is a dimensionless proportionality constant that indicates the degree of magnetization of a material in response to an applied magnetic field...
, Χ. As diamagnetic effects scale with the area of the orbit and the area is proportional to the radius squared (A ∝ n4), effects impossible to detect in ground state atoms become obvious in Rydberg atoms, which demonstrate very large diamagnetic shifts.
Rydberg atoms in plasmas
Rydberg atoms form commonly in plasmaPlasma (physics)
In physics and chemistry, plasma is a state of matter similar to gas in which a certain portion of the particles are ionized. Heating a gas may ionize its molecules or atoms , thus turning it into a plasma, which contains charged particles: positive ions and negative electrons or ions...
s due to the recombination of electrons and positive ions; low energy recombination results in fairly stable Rydberg atoms, while recombination of electrons and positive ions with high kinetic energy
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
often form autoionising
Ionization potential
The ionization energy of a chemical species, i.e. an atom or molecule, is the energy required to remove an electron from the species to a practically infinite distance. Large atoms or molecules have a low ionization energy, while small molecules tend to have higher ionization energies.The property...
Rydberg states. Rydberg atoms’ large sizes and susceptibility to perturbation and ionisation by electric and magnetic fields, are an important factor determining the properties of plasmas.
Condensation of Rydberg atoms forms Rydberg matter
Rydberg matter
Rydberg matter is a phase of matter formed by Rydberg atoms; it was predicted around 1980 by É. A. Manykin, M. I. Ozhovan and P. P. Poluéktov. It has been formed from various elements like caesium, potassium, hydrogen and nitrogen; studies have been conducted on theoretical possibilities like...
most often observed in form of long-lived clusters. The de-excitation is significantly impeded in Rydberg matter by exchange-correlation effects in the non-uniform electron liquid formed on condensation by the collective valence electrons, which causes extended lifetime of clusters.
Rydberg atoms in astrophysics
In the time between the early absorption spectroscopyAbsorption spectroscopy
Absorption spectroscopy refers to spectroscopic techniques that measure the absorption of radiation, as a function of frequency or wavelength, due to its interaction with a sample. The sample absorbs energy, i.e., photons, from the radiating field. The intensity of the absorption varies as a...
experiments and the arrival of tunable lasers, interest in Rydberg atoms was kept alive by the realisation that they are common in interstellar space, and as such are an important radiation source for astronomers.
The density within interstellar gas clouds is typically many orders of magnitude lower than the best laboratory vacuums attainable on Earth, allowing Rydberg atoms to persist for long periods of time without being ionised by collisions or electric and magnetic fields. As a result of this longevity and the abundance of hydrogen it is particularly common for astronomers to observe radiation from the heavens at a frequency of 2.4 GHz, now known to correspond to the hydrogen n = 109 to n = 108 transition. Such a highly excited hydrogen atom on Earth would be ionised almost immediately as the binding energy
Binding energy
Binding energy is the mechanical energy required to disassemble a whole into separate parts. A bound system typically has a lower potential energy than its constituent parts; this is what keeps the system together—often this means that energy is released upon the creation of a bound state...
would be significantly below thermal energies
Thermal energy
Thermal energy is the part of the total internal energy of a thermodynamic system or sample of matter that results in the system's temperature....
.
Strongly interacting systems
Due to their large size, Rydberg atoms can exhibit very large electric dipole momentElectric dipole moment
In physics, the electric dipole moment is a measure of the separation of positive and negative electrical charges in a system of charges, that is, a measure of the charge system's overall polarity with SI units of Coulomb-meter...
s. Calculations using perturbation theory
Perturbation theory (quantum mechanics)
In quantum mechanics, perturbation theory is a set of approximation schemes directly related to mathematical perturbation for describing a complicated quantum system in terms of a simpler one. The idea is to start with a simple system for which a mathematical solution is known, and add an...
show that this results in strong interactions between two close Rydberg atoms. Coherent control of these interactions combined with the their relatively long lifetime makes them a suitable candidate to realize a quantum computer
Quantum computer
A quantum computer is a device for computation that makes direct use of quantum mechanical phenomena, such as superposition and entanglement, to perform operations on data. Quantum computers are different from traditional computers based on transistors...
. , a two-qubit
Qubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
gate
Quantum gate
In quantum computing and specifically the quantum circuit model of computation, a quantum gate is a basic quantum circuit operating on a small number of qubits. They are the building blocks of quantum circuits, like classical logic gates are for conventional digital circuits.Unlike many classical...
has not been achieved experimentally; however, observations of collective excitations or conditional dynamics have been reported, both between two individual atoms and in mesoscopic samples. Strongly interacting Rydberg atoms also feature quantum critical
Quantum Critical Point
A quantum critical point is a special class of continuous phase transition that takes place at the absolute zero of temperature, typically in a material where the phase transition temperature has been driven to zero by the application of a pressure, field or through doping.Conventional phase...
behavior, which makes them interesting to study on their own.
Classical simulation


Planetary orbit
In physics, an orbit is the gravitationally curved path of an object around a point in space, for example the orbit of a planet around the center of a star system, such as the Solar System...
. In the presence of an external electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
Rydberg atoms can obtain very large electric dipole moment
Electric dipole moment
In physics, the electric dipole moment is a measure of the separation of positive and negative electrical charges in a system of charges, that is, a measure of the charge system's overall polarity with SI units of Coulomb-meter...
s making them extremely susceptible to perturbation by the field. Figure 6 shows how application of an external electric field (known in atomic physics as a Stark
Stark effect
The Stark effect is the shifting and splitting of spectral lines of atoms and molecules due to presence of an external static electric field. The amount of splitting and or shifting is called the Stark splitting or Stark shift. In general one distinguishes first- and second-order Stark effects...
field) changes the geometry of the potential, dramatically changing the behaviour of the electron. A Coulombic potential does not apply any torque
Torque
Torque, moment or moment of force , is the tendency of a force to rotate an object about an axis, fulcrum, or pivot. Just as a force is a push or a pull, a torque can be thought of as a twist....
as the force is always antiparallel
Antiparallel (mathematics)
-Definitions:Given two lines m_1 \, and m_2 \,, lines l_1 \, and l_2 \, are anti-parallel with respect to m_1 \, and m_2 \, if \angle 1 = \angle 2 \,....
to the position vector (always pointing along a line running between the electron and the nucleus):
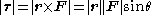 ,
,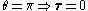 .
.With the application of a static electric field, the electron feels a continuously changing torque. The resulting trajectory becomes progressively more distorted over time, eventually going through the full range of angular momentum from L = LMAX, to a straight line L=0, to the initial orbit in the opposite sense
L = -LMAX.
The time period of the oscillation in angular momentum (the time to complete the trajectory in figure 7), almost exactly matches the quantum mechanically predicted period for the wavefunction to return to its initial state, demonstrating the classical nature of the Rydberg atom.
See also
- Rydberg molecule
- Heavy Rydberg systemHeavy Rydberg systemA heavy Rydberg system consists of a weakly bound positive and negative ion orbiting their common centre of mass. Such systems share many properties with the conventional Rydberg atom and consequently are sometimes referred to as heavy Rydberg atoms...
- Rydberg matterRydberg matterRydberg matter is a phase of matter formed by Rydberg atoms; it was predicted around 1980 by É. A. Manykin, M. I. Ozhovan and P. P. Poluéktov. It has been formed from various elements like caesium, potassium, hydrogen and nitrogen; studies have been conducted on theoretical possibilities like...
- Quantum chaosQuantum chaosQuantum chaos is a branch of physics which studies how chaotic classical dynamical systems can be described in terms of quantum theory. The primary question that quantum chaos seeks to answer is, "What is the relationship between quantum mechanics and classical chaos?" The correspondence principle...

