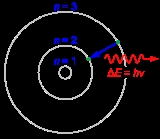
Bohr model
Overview
In atomic physics
Atomic physics
Atomic physics is the field of physics that studies atoms as an isolated system of electrons and an atomic nucleus. It is primarily concerned with the arrangement of electrons around the nucleus and...
, the Bohr model, introduced by Niels Bohr
Niels Bohr
Niels Henrik David Bohr was a Danish physicist who made foundational contributions to understanding atomic structure and quantum mechanics, for which he received the Nobel Prize in Physics in 1922. Bohr mentored and collaborated with many of the top physicists of the century at his institute in...
in 1913, depicts the atom
Atom
The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...
as a small, positively charged nucleus
Atomic nucleus
The nucleus is the very dense region consisting of protons and neutrons at the center of an atom. It was discovered in 1911, as a result of Ernest Rutherford's interpretation of the famous 1909 Rutherford experiment performed by Hans Geiger and Ernest Marsden, under the direction of Rutherford. The...
surrounded by electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
s that travel in circular orbits around the nucleus—similar in structure to the solar system
Solar System
The Solar System consists of the Sun and the astronomical objects gravitationally bound in orbit around it, all of which formed from the collapse of a giant molecular cloud approximately 4.6 billion years ago. The vast majority of the system's mass is in the Sun...
, but with electrostatic forces providing attraction, rather than gravity. This was an improvement on the earlier cubic model (1902), the plum-pudding model (1904), the Saturnian model (1904), and the Rutherford model
Rutherford model
The Rutherford model or planetary model is a model of the atom devised by Ernest Rutherford. Rutherford directed the famous Geiger-Marsden experiment in 1909, which suggested on Rutherford's 1911 analysis that the so-called "plum pudding model" of J. J. Thomson of the atom was incorrect...
(1911).
Unanswered Questions

