
Correspondence principle
Encyclopedia
In physics
, the correspondence principle states that the behavior of systems described by the theory of quantum mechanics
(or by the old quantum theory
) reproduces classical physics
in the limit of large quantum numbers.
The principle was formulated by Niels Bohr
in 1920, though he had previously made use of it as early as 1913 in developing his model of the atom.
The term is also used more generally, to represent the idea that a new theory should reproduce the results of older well-established theories in those domains where the old theories work.
s and elementary particles
. But macroscopic systems like spring
s and capacitor
s are accurately described by classical theories like classical mechanics
and classical electrodynamics
. If quantum mechanics should be applicable to macroscopic objects there must be some limit in which quantum mechanics reduces to classical mechanics. Bohr's correspondence principle demands that classical physics and quantum physics give the same answer when the systems become large.
The conditions under which quantum and classical physics agree are referred to as the correspondence limit, or the classical limit
. Bohr provided a rough prescription for the correspondence limit: it occurs when the quantum numbers describing the system are large. A more elaborated analysis of quantum-classical correspondence (QCC) in wavepacket spreading leads to the distinction between robust "restricted QCC" and fragile "detailed QCC". See and references therein. "Restricted QCC" refers to the first two moments of the probability distribution and is true even when the wave packets diffract, while "detailed QCC" requires smooth potentials which vary over scales much larger than the wavelength, which is what Bohr considered.
The post-1925 new quantum theory came in two different formulations. In matrix mechanics
, the correspondence principle was built in and was used to construct the theory. In the Schrödinger approach
classical behavior is not clear because the waves spread out as they move. Once the Schrödinger equation was given a probabilistic interpretation, Ehrenfest showed that Newton's laws hold on average: the quantum statistical expectation value of the position and momentum obey Newton's laws.
The correspondence principle is one of the tools available to physicists for selecting quantum theories corresponding to reality
. The principles of quantum mechanics
are broad: states of a physical system form a complex vector space
and physical observables are identified with Hermitian operators that act on this Hilbert space. The correspondence principle limits the choices to those that reproduce classical mechanics in the correspondence limit.
Because quantum mechanics only reproduces classical mechanics in a statistical interpretation, and because the statistical interpretation only gives the probabilities of different classical outcomes, Bohr
has argued that classical physics does not emerge from quantum physics in the same way that classical mechanics emerges as an approximation of special relativity
at small velocities
. He argued that classical physics exists independently of quantum theory and cannot be derived from it. His position is that it is inappropriate to understand the experiences of observers using purely quantum mechanical notions such as wavefunctions because the different states of experience of an observer are defined classically, and do not have a quantum mechanical analog.
The relative state interpretation of quantum mechanics is an attempt to understand the experience of observers using only quantum mechanical notions. Niels Bohr was an early opponent of such interpretations.
For example, Einstein's special relativity
satisfies the correspondence principle, because it reduces to classical mechanics in the limit of velocities small compared to the speed of light
(example below). General relativity
reduces to Newtonian gravity in the limit of weak gravitational fields. Laplace's theory of celestial mechanics
reduces to Kepler's when interplanetary interactions are ignored, and Kepler's reproduces Ptolemy's equant
in a coordinate system where the Earth is stationary. Statistical mechanics reproduces thermodynamics when the number of particles is large. In biology, chromosome inheritance theory reproduces Mendel's laws of inheritance, in the domain that the inherited factors are protein coding genes
.
In order for there to be a correspondence, the earlier theory has to have a domain of validity—it must work under some conditions. Not all theories have a domain of validity. For example, there is no limit where Newton's mechanics reduces to Aristotle's mechanics because Aristotle's mechanics, although academically viable for many centuries, do not have any domain of validity.
In quantum mechanics, this emission must be of quanta of light. The frequency of the quanta emitted should be integer multiples of 1/T so that classical mechanics is an approximate description at large quantum numbers. This means that the energy level corresponding to a classical orbit of period 1/T must have nearby energy levels which differ in energy by h/T, and they should be equally spaced near that level:
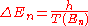
Bohr worried whether the energy spacing 1/T should be best calculated with the period of the energy state or
or 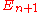 or some average. In hindsight, there is no need to quibble, since this theory is only the leading semiclassical approximation.
or some average. In hindsight, there is no need to quibble, since this theory is only the leading semiclassical approximation.
Bohr considered circular orbits. These orbits must classically decay to smaller circles when they emit photons. The level spacing between circular orbits can be calculated with the correspondence formula. For a hydrogen atom, the classical orbits have a period T which is determined by Kepler's third law to scale as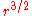 . The energy scales as 1/r, so the level spacing formula says that:
. The energy scales as 1/r, so the level spacing formula says that:
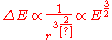
It is possible to determine the energy levels by recursively stepping down orbit by orbit, but there is a shortcut. The angular momentum L of the circular orbit scales as . The energy in terms of the angular momentum is then
. The energy in terms of the angular momentum is then
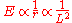
Assuming that quantized values of L are equally spaced, the spacing between neighboring energies is
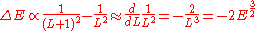
Which is what we want for equally spaced angular momentum. If you keep track of the constants, the spacing is , so the angular momentum should be an integer multiple of
, so the angular momentum should be an integer multiple of 
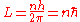
This is how Bohr arrived at his model
. Since only the level spacing is determined by the correspondence principle, you could always add a small fixed offset to the quantum number--- L could just as well have been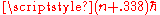 . Bohr used his physical intuition to decide which quantities were best to quantize. It is a testimony to his skill that he was able to get so much from what is only the leading order approximation.
. Bohr used his physical intuition to decide which quantities were best to quantize. It is a testimony to his skill that he was able to get so much from what is only the leading order approximation.
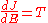
This is the analog of the angular momentum in the case of the circular orbits. The orbits selected by the correspondence principle are the ones that obey J=nh for n integer, since
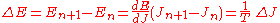
This quantity J is canonically conjugate to a variable θ which, by the Hamilton equations of motion
changes with time as the gradient of energy with J. Since this is equal to the inverse period at all times, the variable θ increases steadily from 0 to 1 over one period.
The angle variable comes back to itself after 1 unit of increase, so the geometry of phase space in J,θ coordinates is that of a half-cylinder, capped off at J = 0, which is the motionless orbit at the lowest value of the energy. These coordinates are just as canonical as x,p, but the orbits are now lines of constant J instead of nested ovoids in x-p space. The area enclosed by an orbit is invariant
under canonical transformations, so it is the same in x-p space as in J-θ. But in the J-θ coordinates this area is the area of a cylinder of unit circumference between 0 and J, or just J. So J is equal to the area enclosed by the orbit in x-p coordinates too:
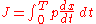
The quantization rule is that the action variable J is an integer multiple of h.
. But both pointed to the same quantity, the action.
Bohr was reluctant to generalize the rule to systems with many degrees of freedom. This step was taken by Sommerfeld, who proposed the general quantization rule for an integrable system:
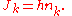
Each action variable is a separate integer, a separate quantum number.
This condition reproduces the circular orbit condition for two dimensional motion: let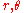 be polar coordinates for a central potential. Then
be polar coordinates for a central potential. Then 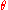 is already an angle variable, and the canonical momentum conjugate is L, the angular momentum. So the quantum condition for L reproduces Bohr's rule:
is already an angle variable, and the canonical momentum conjugate is L, the angular momentum. So the quantum condition for L reproduces Bohr's rule: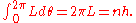
This allowed Sommerfeld to generalize Bohr's theory of circular orbits to elliptical orbits, showing that the energy levels are the same. He also found some general properties of quantum angular momentum which seemed paradoxical at the time. One of these results was the that the z-component of the angular momentum, the classical inclination of an orbit relative to the z-axis, could only take on discrete values, a result which seemed to contradict rotational invariance. This was called space quantization for a while, but this term fell out of favor with the new quantum mechanics since no quantization of space is involved.
In modern quantum mechanics, the principle of superposition makes it clear that rotational invariance is not lost. It is possible to rotate objects with discrete orientations to produce superpositions of other discrete orientations, and this resolves the intuitive paradoxes of the Sommerfeld model.
. Quantum mechanics tells us that the total (kinetic and potential) energy
of the oscillator, E, has a set of discrete values:

where is the angular frequency
is the angular frequency
of the oscillator. However, in a classical harmonic oscillator
such as a lead ball attached to the end of a spring, we do not perceive any discreteness. Instead, the energy of such a macroscopic system appears to vary over a continuum of values.
We can verify that our idea of "macroscopic" systems fall within the correspondence limit. The energy of the classical harmonic oscillator with amplitude
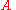 is
is

Thus, the quantum number has the value
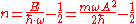
If we apply typical "human-scale" values m = 1kg
, = 1 rad
= 1 rad
/s
, and A = 1m, then n ≈ 4.74×1033. This is a very large number, so the system is indeed in the correspondence limit.
It is simple to see why we perceive a continuum of energy in said limit. With = 1 rad/s, the difference between each energy level is
= 1 rad/s, the difference between each energy level is  J
J
, well below what we can detect.
from special relativity
becomes arbitrarily close to the classical expression for speeds that are much slower than the speed of light
.
Einstein's famous mass-energy equation
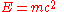
represents the total energy of a body with relativistic mass
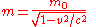
When the velocity is zero, the energy expressed above is not zero and represents the rest energy:
is zero, the energy expressed above is not zero and represents the rest energy:
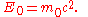
When the body is in motion relative to the observer, the total energy exceeds the rest energy by an amount that is, by definition, the kinetic energy:
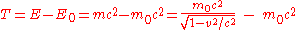
Using the approximation
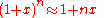
we get when speeds are much slower than that of light or
which is the Newtonian
expression for kinetic energy
.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the correspondence principle states that the behavior of systems described by the theory of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
(or by the old quantum theory
Old quantum theory
The old quantum theory was a collection of results from the years 1900–1925 which predate modern quantum mechanics. The theory was never complete or self-consistent, but was a collection of heuristic prescriptions which are now understood to be the first quantum corrections to classical mechanics...
) reproduces classical physics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
in the limit of large quantum numbers.
The principle was formulated by Niels Bohr
Niels Bohr
Niels Henrik David Bohr was a Danish physicist who made foundational contributions to understanding atomic structure and quantum mechanics, for which he received the Nobel Prize in Physics in 1922. Bohr mentored and collaborated with many of the top physicists of the century at his institute in...
in 1920, though he had previously made use of it as early as 1913 in developing his model of the atom.
The term is also used more generally, to represent the idea that a new theory should reproduce the results of older well-established theories in those domains where the old theories work.
Quantum mechanics
The rules of quantum mechanics are highly successful in describing microscopic objects, atomAtom
The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...
s and elementary particles
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
. But macroscopic systems like spring
Spring (device)
A spring is an elastic object used to store mechanical energy. Springs are usually made out of spring steel. Small springs can be wound from pre-hardened stock, while larger ones are made from annealed steel and hardened after fabrication...
s and capacitor
Capacitor
A capacitor is a passive two-terminal electrical component used to store energy in an electric field. The forms of practical capacitors vary widely, but all contain at least two electrical conductors separated by a dielectric ; for example, one common construction consists of metal foils separated...
s are accurately described by classical theories like classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
and classical electrodynamics
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
. If quantum mechanics should be applicable to macroscopic objects there must be some limit in which quantum mechanics reduces to classical mechanics. Bohr's correspondence principle demands that classical physics and quantum physics give the same answer when the systems become large.
The conditions under which quantum and classical physics agree are referred to as the correspondence limit, or the classical limit
Classical limit
The classical limit or correspondence limit is the ability of a physical theory to approximate or "recover" classical mechanics when considered over special values of its parameters. The classical limit is used with physical theories that predict non-classical behavior...
. Bohr provided a rough prescription for the correspondence limit: it occurs when the quantum numbers describing the system are large. A more elaborated analysis of quantum-classical correspondence (QCC) in wavepacket spreading leads to the distinction between robust "restricted QCC" and fragile "detailed QCC". See and references therein. "Restricted QCC" refers to the first two moments of the probability distribution and is true even when the wave packets diffract, while "detailed QCC" requires smooth potentials which vary over scales much larger than the wavelength, which is what Bohr considered.
The post-1925 new quantum theory came in two different formulations. In matrix mechanics
Matrix mechanics
Matrix mechanics is a formulation of quantum mechanics created by Werner Heisenberg, Max Born, and Pascual Jordan in 1925.Matrix mechanics was the first conceptually autonomous and logically consistent formulation of quantum mechanics. It extended the Bohr Model by describing how the quantum jumps...
, the correspondence principle was built in and was used to construct the theory. In the Schrödinger approach
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
classical behavior is not clear because the waves spread out as they move. Once the Schrödinger equation was given a probabilistic interpretation, Ehrenfest showed that Newton's laws hold on average: the quantum statistical expectation value of the position and momentum obey Newton's laws.
The correspondence principle is one of the tools available to physicists for selecting quantum theories corresponding to reality
Reality
In philosophy, reality is the state of things as they actually exist, rather than as they may appear or might be imagined. In a wider definition, reality includes everything that is and has been, whether or not it is observable or comprehensible...
. The principles of quantum mechanics
Mathematical formulation of quantum mechanics
The mathematical formulations of quantum mechanics are those mathematical formalisms that permit a rigorous description of quantum mechanics. Such are distinguished from mathematical formalisms for theories developed prior to the early 1900s by the use of abstract mathematical structures, such as...
are broad: states of a physical system form a complex vector space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
and physical observables are identified with Hermitian operators that act on this Hilbert space. The correspondence principle limits the choices to those that reproduce classical mechanics in the correspondence limit.
Because quantum mechanics only reproduces classical mechanics in a statistical interpretation, and because the statistical interpretation only gives the probabilities of different classical outcomes, Bohr
Niels Bohr
Niels Henrik David Bohr was a Danish physicist who made foundational contributions to understanding atomic structure and quantum mechanics, for which he received the Nobel Prize in Physics in 1922. Bohr mentored and collaborated with many of the top physicists of the century at his institute in...
has argued that classical physics does not emerge from quantum physics in the same way that classical mechanics emerges as an approximation of special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
at small velocities
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
. He argued that classical physics exists independently of quantum theory and cannot be derived from it. His position is that it is inappropriate to understand the experiences of observers using purely quantum mechanical notions such as wavefunctions because the different states of experience of an observer are defined classically, and do not have a quantum mechanical analog.
The relative state interpretation of quantum mechanics is an attempt to understand the experience of observers using only quantum mechanical notions. Niels Bohr was an early opponent of such interpretations.
Other scientific theories
The term "correspondence principle" is used in a more general sense to mean the reduction of a new scientific theory to an earlier scientific theory in appropriate circumstances. This requires that the new theory explain all the phenomena under circumstances for which the preceding theory was known to be valid, the "correspondence limit".For example, Einstein's special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
satisfies the correspondence principle, because it reduces to classical mechanics in the limit of velocities small compared to the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
(example below). General relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
reduces to Newtonian gravity in the limit of weak gravitational fields. Laplace's theory of celestial mechanics
Celestial mechanics
Celestial mechanics is the branch of astronomy that deals with the motions of celestial objects. The field applies principles of physics, historically classical mechanics, to astronomical objects such as stars and planets to produce ephemeris data. Orbital mechanics is a subfield which focuses on...
reduces to Kepler's when interplanetary interactions are ignored, and Kepler's reproduces Ptolemy's equant
Equant
Equant is a mathematical concept developed by Claudius Ptolemy in the 2nd century AD to account for the observed motion of heavenly bodies....
in a coordinate system where the Earth is stationary. Statistical mechanics reproduces thermodynamics when the number of particles is large. In biology, chromosome inheritance theory reproduces Mendel's laws of inheritance, in the domain that the inherited factors are protein coding genes
Gênes
Gênes is the name of a département of the First French Empire in present Italy, named after the city of Genoa. It was formed in 1805, when Napoleon Bonaparte occupied the Republic of Genoa. Its capital was Genoa, and it was divided in the arrondissements of Genoa, Bobbio, Novi Ligure, Tortona and...
.
In order for there to be a correspondence, the earlier theory has to have a domain of validity—it must work under some conditions. Not all theories have a domain of validity. For example, there is no limit where Newton's mechanics reduces to Aristotle's mechanics because Aristotle's mechanics, although academically viable for many centuries, do not have any domain of validity.
Bohr model
If an electron in an atom is moving on an orbit with period T, the electromagnetic radiation will classically repeat itself every orbital period. If the coupling to the electromagnetic field is weak, so that the orbit doesn't decay very much in one cycle, the radiation will be emitted in a pattern which repeats every period, so that the fourier transform will have frequencies which are only multiples of 1/T. This is the classical radiation law: the frequencies emitted are integer multiples of 1/T.In quantum mechanics, this emission must be of quanta of light. The frequency of the quanta emitted should be integer multiples of 1/T so that classical mechanics is an approximate description at large quantum numbers. This means that the energy level corresponding to a classical orbit of period 1/T must have nearby energy levels which differ in energy by h/T, and they should be equally spaced near that level:
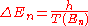
Bohr worried whether the energy spacing 1/T should be best calculated with the period of the energy state
 or
or 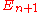 or some average. In hindsight, there is no need to quibble, since this theory is only the leading semiclassical approximation.
or some average. In hindsight, there is no need to quibble, since this theory is only the leading semiclassical approximation.Bohr considered circular orbits. These orbits must classically decay to smaller circles when they emit photons. The level spacing between circular orbits can be calculated with the correspondence formula. For a hydrogen atom, the classical orbits have a period T which is determined by Kepler's third law to scale as
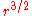 . The energy scales as 1/r, so the level spacing formula says that:
. The energy scales as 1/r, so the level spacing formula says that: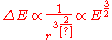
It is possible to determine the energy levels by recursively stepping down orbit by orbit, but there is a shortcut. The angular momentum L of the circular orbit scales as
 . The energy in terms of the angular momentum is then
. The energy in terms of the angular momentum is then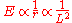
Assuming that quantized values of L are equally spaced, the spacing between neighboring energies is
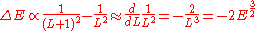
Which is what we want for equally spaced angular momentum. If you keep track of the constants, the spacing is
 , so the angular momentum should be an integer multiple of
, so the angular momentum should be an integer multiple of 
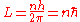
This is how Bohr arrived at his model
Bohr model
In atomic physics, the Bohr model, introduced by Niels Bohr in 1913, depicts the atom as a small, positively charged nucleus surrounded by electrons that travel in circular orbits around the nucleus—similar in structure to the solar system, but with electrostatic forces providing attraction,...
. Since only the level spacing is determined by the correspondence principle, you could always add a small fixed offset to the quantum number--- L could just as well have been
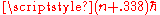 . Bohr used his physical intuition to decide which quantities were best to quantize. It is a testimony to his skill that he was able to get so much from what is only the leading order approximation.
. Bohr used his physical intuition to decide which quantities were best to quantize. It is a testimony to his skill that he was able to get so much from what is only the leading order approximation.One-dimensional potential
Bohr's correspondence condition can be solved for the level energies in a general one-dimensional potential. Define a quantity J(E) which is a function only of the energy, and has the property that: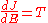
This is the analog of the angular momentum in the case of the circular orbits. The orbits selected by the correspondence principle are the ones that obey J=nh for n integer, since
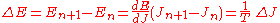
This quantity J is canonically conjugate to a variable θ which, by the Hamilton equations of motion
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
changes with time as the gradient of energy with J. Since this is equal to the inverse period at all times, the variable θ increases steadily from 0 to 1 over one period.
The angle variable comes back to itself after 1 unit of increase, so the geometry of phase space in J,θ coordinates is that of a half-cylinder, capped off at J = 0, which is the motionless orbit at the lowest value of the energy. These coordinates are just as canonical as x,p, but the orbits are now lines of constant J instead of nested ovoids in x-p space. The area enclosed by an orbit is invariant
Liouville's theorem
Liouville's theorem has various meanings, all mathematical results named after Joseph Liouville:*In complex analysis, see Liouville's theorem ; there is also a related theorem on harmonic functions....
under canonical transformations, so it is the same in x-p space as in J-θ. But in the J-θ coordinates this area is the area of a cylinder of unit circumference between 0 and J, or just J. So J is equal to the area enclosed by the orbit in x-p coordinates too:
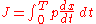
The quantization rule is that the action variable J is an integer multiple of h.
Multiperiodic motion—Bohr–Sommerfeld quantization
Bohr's correspondence principle provided a way to find the semiclassical quantization rule for a one degree of freedom system. It was an argument for the old quantum condition mostly independent from the one developed by Wien and Einstein, which focused on adiabatic invarianceAdiabatic invariant
An adiabatic invariant is a property of a physical system that stays constant when changes occur slowly.In thermodynamics, an adiabatic process is a change that occurs without heat flow, and slowly compared to the time to reach equilibrium. In an adiabatic process, the system is in equilibrium at...
. But both pointed to the same quantity, the action.
Bohr was reluctant to generalize the rule to systems with many degrees of freedom. This step was taken by Sommerfeld, who proposed the general quantization rule for an integrable system:
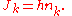
Each action variable is a separate integer, a separate quantum number.
This condition reproduces the circular orbit condition for two dimensional motion: let
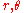 be polar coordinates for a central potential. Then
be polar coordinates for a central potential. Then 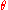 is already an angle variable, and the canonical momentum conjugate is L, the angular momentum. So the quantum condition for L reproduces Bohr's rule:
is already an angle variable, and the canonical momentum conjugate is L, the angular momentum. So the quantum condition for L reproduces Bohr's rule: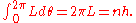
This allowed Sommerfeld to generalize Bohr's theory of circular orbits to elliptical orbits, showing that the energy levels are the same. He also found some general properties of quantum angular momentum which seemed paradoxical at the time. One of these results was the that the z-component of the angular momentum, the classical inclination of an orbit relative to the z-axis, could only take on discrete values, a result which seemed to contradict rotational invariance. This was called space quantization for a while, but this term fell out of favor with the new quantum mechanics since no quantization of space is involved.
In modern quantum mechanics, the principle of superposition makes it clear that rotational invariance is not lost. It is possible to rotate objects with discrete orientations to produce superpositions of other discrete orientations, and this resolves the intuitive paradoxes of the Sommerfeld model.
The quantum harmonic oscillator
We provide a demonstration of how large quantum numbers can give rise to classical (continuous) behavior. Consider the one-dimensional quantum harmonic oscillatorQuantum harmonic oscillator
The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary potential can be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics...
. Quantum mechanics tells us that the total (kinetic and potential) energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
of the oscillator, E, has a set of discrete values:

where
 is the angular frequency
is the angular frequencyAngular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
of the oscillator. However, in a classical harmonic oscillator
Harmonic oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force, F, proportional to the displacement, x: \vec F = -k \vec x \, where k is a positive constant....
such as a lead ball attached to the end of a spring, we do not perceive any discreteness. Instead, the energy of such a macroscopic system appears to vary over a continuum of values.
We can verify that our idea of "macroscopic" systems fall within the correspondence limit. The energy of the classical harmonic oscillator with amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
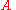 is
is
Thus, the quantum number has the value
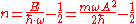
If we apply typical "human-scale" values m = 1kg
Kilogram
The kilogram or kilogramme , also known as the kilo, is the base unit of mass in the International System of Units and is defined as being equal to the mass of the International Prototype Kilogram , which is almost exactly equal to the mass of one liter of water...
,
 = 1 rad
= 1 radRadian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
/s
Second
The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock....
, and A = 1m, then n ≈ 4.74×1033. This is a very large number, so the system is indeed in the correspondence limit.
It is simple to see why we perceive a continuum of energy in said limit. With
 = 1 rad/s, the difference between each energy level is
= 1 rad/s, the difference between each energy level is  J
JJoule
The joule ; symbol J) is a derived unit of energy or work in the International System of Units. It is equal to the energy expended in applying a force of one newton through a distance of one metre , or in passing an electric current of one ampere through a resistance of one ohm for one second...
, well below what we can detect.
Relativistic kinetic energy
Here we show that the expression of kinetic energyKinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
from special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
becomes arbitrarily close to the classical expression for speeds that are much slower than the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
.
Einstein's famous mass-energy equation
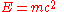
represents the total energy of a body with relativistic mass
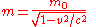
- where the velocity,
 is the velocity of the body relative to the observer,
is the velocity of the body relative to the observer,  is the rest mass (the observed mass of the body at zero velocity relative to the observer), and
is the rest mass (the observed mass of the body at zero velocity relative to the observer), and  is the speed of lightSpeed of lightThe speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
is the speed of lightSpeed of lightThe speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
.
When the velocity
 is zero, the energy expressed above is not zero and represents the rest energy:
is zero, the energy expressed above is not zero and represents the rest energy: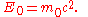
When the body is in motion relative to the observer, the total energy exceeds the rest energy by an amount that is, by definition, the kinetic energy:
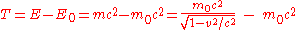
Using the approximation
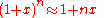
-
-
- for

- for
-
we get when speeds are much slower than that of light or

 |
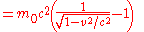 |
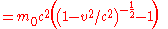 |
|
 |
|
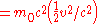 |
|
 |
which is the Newtonian
Classical physics
What "classical physics" refers to depends on the context. When discussing special relativity, it refers to the Newtonian physics which preceded relativity, i.e. the branches of physics based on principles developed before the rise of relativity and quantum mechanics...
expression for kinetic energy
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
.

