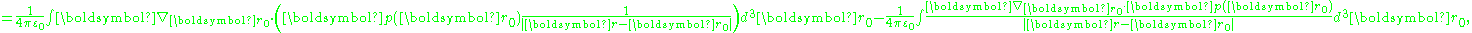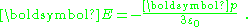Electric dipole moment
Encyclopedia

Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the electric dipole moment is a measure of the separation of positive and negative electrical charges in a system of charges, that is, a measure of the charge system's overall polarity
Chemical polarity
In chemistry, polarity refers to a separation of electric charge leading to a molecule or its chemical groups having an electric dipole or multipole moment. Polar molecules interact through dipole–dipole intermolecular forces and hydrogen bonds. Molecular polarity is dependent on the difference in...
with SI units of Coulomb-meter (C m). This article is limited to static phenomena, and does not describe time-dependent or dynamic polarization.
In the simple case of two point charges, one with charge +q and one with charge −q, the electric dipole moment p is:
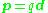
where d is the displacement vector
Displacement (vector)
A displacement is the shortest distance from the initial to the final position of a point P. Thus, it is the length of an imaginary straight path, typically distinct from the path actually travelled by P...
pointing from the negative charge to the positive charge. Thus, the electric dipole moment vector p points from the negative charge to the positive charge. There is no inconsistency here, because the electric dipole moment has to do with orientation of the dipole, that is, the positions of the charges, and does not indicate the direction of the field originating in these charges.
An idealization of this two-charge system is the electrical point dipole consisting of two (infinite) charges only infinitesimally separated, but with a finite p = qd.
An object with an electric dipole moment is subject to a torque
Torque
Torque, moment or moment of force , is the tendency of a force to rotate an object about an axis, fulcrum, or pivot. Just as a force is a push or a pull, a torque can be thought of as a twist....
τ when placed in an external electric field. The torque tends to align the dipole with the field, and makes alignment an orientation of lower potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
than misalignment. For a spatially uniform electric field E, the torque is given by:
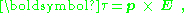
where p is the dipole moment, and the symbol "×" refers to the vector cross product. The field vector and the dipole vector define a plane, and the torque is directed normal to that plane with the direction given by the right-hand rule
Right-hand rule
In mathematics and physics, the right-hand rule is a common mnemonic for understanding notation conventions for vectors in 3 dimensions. It was invented for use in electromagnetism by British physicist John Ambrose Fleming in the late 19th century....
.
General case
More generally, for a continuous distribution of charge confined to a volume V, the corresponding expression for the dipole moment is: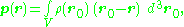
where r locates the point of observation and d3r0 denotes an elementary volume in V. For an array of point charges, the charge density becomes a sum of Dirac delta function
Dirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
s:
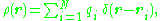
where each ri is a vector from some reference point to the charge qi. Substitution into the above integration formula provides:
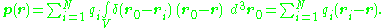
This expression is equivalent to the previous expression in the case of charge neutrality and
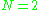 . For two opposite charges, denoting the location of the positive charge of the pair as r+ and the location of the negative charge as r−:
. For two opposite charges, denoting the location of the positive charge of the pair as r+ and the location of the negative charge as r−: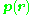

showing that the dipole moment vector is directed from the negative charge to the positive charge because the position vector of a point is directed outward from the origin to that point.
The dipole moment is most easily understood when the system has an overall neutral charge; for example, a pair of opposite charges, or a neutral conductor in a uniform electric field. For a system of charges with no net charge, visualized as an array of paired opposite charges, the relation for electric dipole moment is:

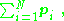
which is the vector sum of the individual dipole moments of the neutral charge pairs. (Because of overall charge neutrality, the dipole moment is independent of the observer's position r.) Thus, the value of p is independent of the choice of reference point, provided the overall charge of the system is zero.
When discussing the dipole moment of a non-neutral system, such as the dipole moment of the proton
Proton
The proton is a subatomic particle with the symbol or and a positive electric charge of 1 elementary charge. One or more protons are present in the nucleus of each atom, along with neutrons. The number of protons in each atom is its atomic number....
, a dependence on the choice of reference point arises. In such cases it is conventional to choose the reference point to be the center of mass
Center of mass
In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body...
of the system, not some arbitrary origin.
It might seem that the center of charge is more reasonable reference point than the center of mass, but it is clear that this results in a zero dipole moment. This convention ensures that the dipole moment is an intrinsic property of the system.
Potential and field of an electric dipole
An ideal dipole consists of two opposite charges with infinitesimal separation. The potential and field of such an ideal dipole are found next as a limiting case of an example of two opposite charges at non-zero separation.Two closely spaced opposite charges have a potential of the form:
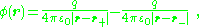
with charge separation, d, defined as

The radius to the center of charge, R, and the unit vector in the direction of R are given by:
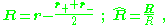
Taylor expansion in d/r (see multipole expansion
Multipole expansion
A multipole expansion is a mathematical series representing a function that depends on angles — usually the two angles on a sphere. These series are useful because they can often be truncated, meaning that only the first few terms need to be retained for a good approximation to the original...
and quadrupole) allows this potential to be expressed as a series.
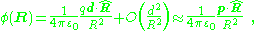
where higher order terms in the series are vanishing at large distances, R, compared to d. Here, the electric dipole moment p is, as above:

The result for the dipole potential also can be expressed as:
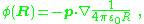
which relates the dipole potential to that of a point charge. A key point is that the potential of the dipole falls off faster with distance R than that of the point charge.
The electric field of the dipole is the negative gradient of the potential, leading to:
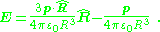
Thus, although two closely spaced opposite charges are not an ideal electric dipole (because their potential at close approach is not that of a dipole), at distances much larger than their separation, their dipole moment p appears directly in their potential and field.
As the two charges are brought closer together (d is made smaller), the dipole term in the multipole expansion based on the ratio d/R becomes the only significant term at ever closer distances R, and in the limit of infinitesimal separation the dipole term in this expansion is all that matters. As d is made infinitesimal, however, the dipole charge must be made to increase to hold p constant. This limiting process results in a "point dipole".
Dipole moment density and polarization density
The dipole moment of an array of charge,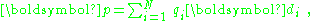
determines the degree of polarity of the array, but for a neutral array it is simply a vector property of the array with no directions about where the array happens to be located. The dipole moment density of the array p(r) contains both the location of the array and its dipole moment. When it comes time to calculate the electric field in some region containing the array, Maxwell's equations are solved, and the information about the charge array is contained in the polarization density P(r) of Maxwell's equations. Depending upon how fine-grained an assessment of the electric field is required, more or less information about the charge array will have to be expressed by P(r). As explained below, sometimes it is sufficiently accurate to take P(r) = p(r). Sometimes a more detailed description is needed (for example, supplementing the dipole moment density with an additional quadrupole density) and sometimes even more elaborate versions of P(r) are necessary.
It now is explored just in what way the polarization density P(r) that enters Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
is related to the dipole moment p of an overall neutral array of charges, and also to the dipole moment density p(r) (which describes not only the dipole moment, but also the array location). Only static situations are considered in what follows, so P has no time dependence, and there is no displacement current
Displacement current
In electromagnetism, displacement current is a quantity that is defined in terms of the rate of change of electric displacement field. Displacement current has the units of electric current density, and it has an associated magnetic field just as actual currents do. However it is not an electric...
. First is some discussion of the polarization density P(r). That discussion is followed with several particular examples.
A formulation of Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
based upon division of charges and currents into "free" and "bound" charges and currents leads to introduction of the D- and P-fields:

where P is called the polarization density
Polarization density
In classical electromagnetism, polarization density is the vector field that expresses the density of permanent or induced electric dipole moments in a dielectric material. When a dielectric is placed in an external electric field, its molecules gain electric dipole moment and the dielectric is...
. In this formulation, the divergence of this equation yields:
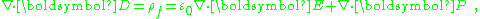
and as the divergence term in E is the total charge, and ρf is "free charge", we are left with the relation:

with ρb as the bound charge, by which is meant the difference between the total and the free charge densities.
As an aside, in the absence of magnetic effects, Maxwell's equations specify that curl E = 0, which implies curl (D − P) = 0. Applying Helmholtz decomposition
Helmholtz decomposition
In physics and mathematics, in the area of vector calculus, Helmholtz's theorem, also known as the fundamental theorem of vector calculus, states that any sufficiently smooth, rapidly decaying vector field in three dimensions can be resolved into the sum of an irrotational vector field and a...
:
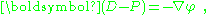
for some scalar potential φ, and:

Suppose the charges are divided into free and bound, and the potential is divided into φ = φf + φb. Satisfaction of the boundary conditions upon φ may be divided arbitrarily between φf and φb because only the sum φ must satisfy these conditions. It follows that P is simply proportional to the electric field due to the charges selected as bound, with boundary conditions that prove convenient. In particular, when no free charge is present, one possible choice is P = ε0 E.
Next is discussed how several different dipole-moment descriptions of a medium relate to the polarization entering Maxwell's equations.
Medium with charge and dipole densities
As described next, a model for polarization moment density p(r) results in a polarization P(r) = p(r) restricted to the same model. For a smoothly varying dipole moment distribution p(r), the corresponding bound charge density is simply ∇·p(r) = −ρb. However, in the case of a p(r) that exhibits an abrupt step in dipole moment at a boundary between two regions, ∇·p(r) exhibits a surface charge component of bound charge. This surface charge can be treated through a surface integral, or by using discontinuity conditions at the boundary, as illustrated in the various examples below.As a first example relating dipole moment to polarization, consider a medium made up of a continuous charge density ρ(r) and a continuous dipole moment distribution p(r). The potential at a position r is:
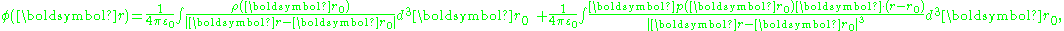
where ρ(r) is the unpaired charge density, and p(r) is the dipole moment density. Using an identity:

the polarization integral can be transformed:
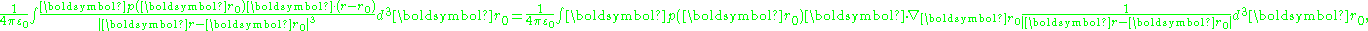
The first term can be transformed to an integral over the surface bounding the volume of integration, and contributes a surface charge density, discussed later. Putting this result back into the potential, and ignoring the surface charge for now:
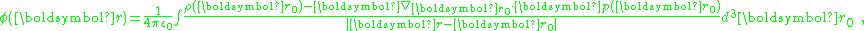
where the volume integration extends only up to the bounding surface, and does not include this surface.
The potential is determined by the total charge, which the above shows consists of:
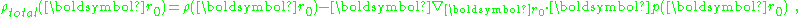
showing that:
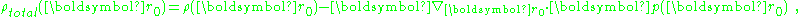
In short, the dipole moment density p(r) plays the role of the polarization density P for this medium. Notice, p(r) has a non-zero divergence equal to the bound charge density (as modeled in this approximation).
It may be noted that this approach can be extended to include all the multipoles: dipole, quadrupole, etc. Using the relation:
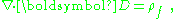
the polarization density is found to be:

where the added terms are meant to indicate contributions from higher multipoles. Evidently, inclusion of higher multipoles signifies that the polarization density P no longer is determined by a dipole moment density p. For example, in considering scattering from a charge array, different multipoles scatter an electromagnetic wave differently and independently, requiring a representation of the charges that goes beyond the dipole approximation.
Surface charge
Above, discussion was deferred for the leading divergence term in the expression for the potential due to the dipoles. This term results in a surface charge.The figure at the right provides an intuitive idea of why a surface charge arises. The figure shows a uniform array of identical dipoles between two surfaces. Internally, the heads and tails of dipoles are adjacent and cancel. At the bounding surfaces, however, no cancellation occurs. Instead, on one surface the dipole heads create a positive surface charge, while at the opposite surface the dipole tails create a negative surface charge. These two opposite surface charges create a net electric field in a direction opposite to the direction of the dipoles.
This idea is given mathematical form using the potential expression above. The potential is:
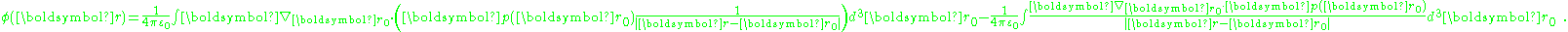
Using the divergence theorem
Divergence theorem
In vector calculus, the divergence theorem, also known as Gauss' theorem , Ostrogradsky's theorem , or Gauss–Ostrogradsky theorem is a result that relates the flow of a vector field through a surface to the behavior of the vector field inside the surface.More precisely, the divergence theorem...
, the divergence term transforms into the surface integral:
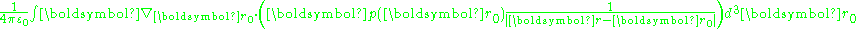
with dAo an element of surface area of the volume. In the event that p(r) is a constant, only the surface term survives:

with dAo an elementary area of the surface bounding the charges. In words, the potential due to a constant p inside the surface is equivalent to that of a surface charge σ = p·dA, which is positive for surface elements with a component in the direction of p and negative for surface elements pointed oppositely. (Usually the direction of a surface element is taken to be that of the outward normal to the surface at the location of the element.)
If the bounding surface is a sphere, and the point of observation is at the center of this sphere, the integration over the surface of the sphere is zero: the positive and negative surface charge contributions to the potential cancel. If the point of observation is off-center, however, a net potential can result (depending upon the situation) because the positive and negative charges are at different distances from the point of observation. The field due to the surface charge is:
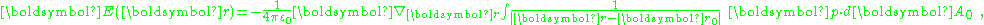
which, at the center of a spherical bounding surface is not zero (the fields of negative and positive charges on opposite sides of the center add because both fields point the same way) but is instead :
If we suppose the polarization of the dipoles was induced by an external field, the polarization field opposes the applied field and sometimes is called a depolarization field. In the case when the polarization is outside a spherical cavity, the field in the cavity due to the surrounding dipoles is in the same direction as the polarization.
In particular, if the electric susceptibility
Electric susceptibility
In electromagnetism, the electric susceptibility \chi_e is a dimensionless proportionality constant that indicates the degree of polarization of a dielectric material in response to an applied electric field...
is introduced through the approximation:
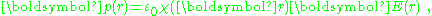
then:

Whenever χ (r) is used to model a step discontinuity at the boundary between two regions, the step produces a surface charge layer. For example, integrating along a normal to the bounding surface from a point just interior to one surface to another point just exterior:
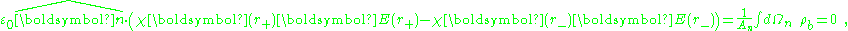
where An, Ωn indicate the area and volume of an elementary region straddling the boundary between the regions, and
 a unit normal to the surface. The right side vanishes as the volume shrinks, inasmuch as ρb is finite, indicating a discontinuity in E, and therefore a surface charge. That is, where the modeled medium includes a step in permittivity, the polarization density corresponding to the dipole moment density p(r) = χ(r)E(r) necessarily includes the contribution of a surface charge.
a unit normal to the surface. The right side vanishes as the volume shrinks, inasmuch as ρb is finite, indicating a discontinuity in E, and therefore a surface charge. That is, where the modeled medium includes a step in permittivity, the polarization density corresponding to the dipole moment density p(r) = χ(r)E(r) necessarily includes the contribution of a surface charge.It may be noted that a physically more realistic modeling of p(r) would cause the dipole moment density to taper off continuously to zero at the boundary of the confining region, rather than making a sudden step to zero density. Then the surface charge becomes zero at the boundary, and the surface charge is replaced by the divergence of a continuously varying dipole-moment density.
Dielectric sphere in uniform external electric field
The above general remarks about surface charge are made more concrete by considering the example of a dielectric sphere in a uniform electric field. The sphere is found to adopt a surface charge related to the dipole moment of its interior.A uniform external electric field is supposed to point in the z-direction, and spherical-polar coordinates are introduced so the potential created by this field is:
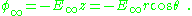
The sphere is assumed to be described by a dielectric constant κ, that is, D = κε0E, and inside the sphere the potential satisfies Laplace's equation. Skipping a few details, the solution inside the sphere is:
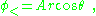
while outside the sphere:

At large distances, φ> → φ∞ so B = -E∞ . Continuity of potential and of the radial component of displacement D = κε0E determine the other two constants. Supposing the radius of the sphere is R,

As a consequence, the potential is:
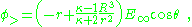
which is the potential due to applied field and, in addition, a dipole in the direction of the applied field (the z-direction) of dipole moment:
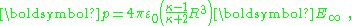
or, per unit volume:
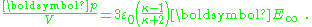
The factor (κ-1)/(κ+2) is called the Clausius-Mossotti factor and shows that the induced polarization flips sign if κ < 1. Of course, this cannot happen in this example, but in an example with two different dielectrics κ is replaced by the ratio of the inner to outer region dielectric constants, which can be greater or smaller than one. The potential inside the sphere is:
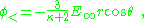
leading to the field inside the sphere:

showing the depolarizing effect of the dipole. Notice that the field inside the sphere is uniform and parallel to the applied field. The dipole moment is uniform throughout the interior of the sphere. The surface charge density on the sphere is the difference between the radial field components:

This linear dielectric example shows that the dielectric constant treatment is equivalent to the uniform dipole-moment model and leads to zero charge everywhere except for the surface charge at the boundary of the sphere.
General media
If observation is confined to regions sufficiently remote from a system of charges, a multipole expansion of the exact polarization density can be made. By truncating this expansion (for example, retaining only the dipole terms, or only the dipole and quadrupole terms, or etc.), the results of the previous section are regained. In particular, truncating the expansion at the dipole term, the result is indistinguishable from the polarization density generated by a uniform dipole moment confined to the charge region. To the accuracy of this dipole approximation, as shown in the previous section, the dipole moment density p(r) (which includes not only p but the location of p) serves as P(r).At locations inside the charge array, to connect an array of paired charges to an approximation involving only a dipole moment density p(r) requires additional considerations. The simplest approximation is to replace the charge array with a model of ideal (infinitesimally spaced) dipoles. In particular, as in the example above that uses a constant dipole moment density confined to a finite region, a surface charge and depolarization field results. A more general version of this model (which allows the polarization to vary with position) is the customary approach using a electric susceptibility
Electric susceptibility
In electromagnetism, the electric susceptibility \chi_e is a dimensionless proportionality constant that indicates the degree of polarization of a dielectric material in response to an applied electric field...
or electrical permittivity.
A more complex model of the point charge array introduces an effective medium
Effective Medium Approximations
Effective medium approximations or effective medium theory are physical models that describe the macroscopic properties of a medium based on the properties and the relative fractions of its components...
by averaging the microscopic charges; for example, the averaging can arrange that only dipole fields play a role. A related approach is to divide the charges into those nearby the point of observation, and those far enough away to allow a multipole expansion. The nearby charges then give rise to local field effects. In a common model of this type, the distant charges are treated as a homogeneous medium using a dielectric constant, and the nearby charges are treated only in a dipole approximation. The approximation of a medium or an array of charges by only dipoles and their associated dipole moment density is sometimes called the point dipole approximation, the discrete dipole approximation
Discrete dipole approximation
The discrete dipole approximation is a method for computing scattering of radiation by particles of arbitrary shape and by periodic structures. Given a target of arbitrary geometry, one seeks to calculate its scattering and absorption properties...
, or simply the dipole approximation.
Dipole moments of fundamental particles
Much experimental work is continuing on measuring the electric dipole moments (EDM) of fundamental and composite particles, namely those of the neutronNeutron
The neutron is a subatomic hadron particle which has the symbol or , no net electric charge and a mass slightly larger than that of a proton. With the exception of hydrogen, nuclei of atoms consist of protons and neutrons, which are therefore collectively referred to as nucleons. The number of...
and electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
. As EDMs violate both the Parity
Parity (physics)
In physics, a parity transformation is the flip in the sign of one spatial coordinate. In three dimensions, it is also commonly described by the simultaneous flip in the sign of all three spatial coordinates:...
(P) and Time (T) symmetries, their values yield a mostly model-independent measure (assuming CPT symmetry
CPT symmetry
CPT symmetry is a fundamental symmetry of physical laws under transformations that involve the inversions of charge, parity, and time simultaneously.-History:...
is valid) of CP-violation in nature. Therefore, values for these EDMs place strong constraints upon the scale of CP-violation that extensions to the standard model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
of particle physics
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
may allow.
Indeed, many theories are inconsistent with the current limits and have effectively been ruled out, and established theory permits a much larger value than these limits, leading to the strong CP problem and prompting searches for new particles such as the axion
Axion
The axion is a hypothetical elementary particle postulated by the Peccei-Quinn theory in 1977 to resolve the strong CP problem in quantum chromodynamics...
.
Current generations of experiments are designed to be sensitive to the supersymmetry
Supersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
range of EDMs, providing complementary experiments to those done at the LHC
LHC
LHC may refer to:* Large Hadron Collider, a particle accelerator and collider located on the Franco-Swiss border near Geneva, SwitzerlandLHC also may refer to:* La hora Chanante, a Spanish comedy television show...
.
Dipole moments of Molecules
Dipole moments in molecules are responsible for the behavior of a substance in the presence ofexternal fields. The dipoles tend to be aligned to the external field which can be constant or
time-dependent. This effect forms the basis of a modern experimental technique called
Dielectric spectroscopy
Dielectric spectroscopy
Dielectric spectroscopy , and also known as electrochemical impedance spectroscopy, measures the dielectric properties of a medium as a function of frequency...
.
Dipole moments can be found in common molecules such as water and also in biomolecules such as
proteins.
By means of the total dipole moment of some material one can compute the dielectric constant which
is related to the more intuitive concept of conductivity.
If
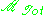 is the total dipole moment of the sample, then the dielectric
is the total dipole moment of the sample, then the dielectricconstant is given by,
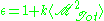
where
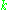 is a constant and
is a constant and 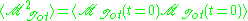 is the time correlation function of the total dipole moment. In general the total dipole moment have contributions coming
is the time correlation function of the total dipole moment. In general the total dipole moment have contributions comingfrom translations and rotations of the molecules in the sample,
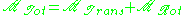
Therefore, the dielectric constant (and the conductivity) has contributions from both terms.
This approach can be generalized to compute the frequency dependent dielectric function.
Further reading
See also
- DipoleDipoleIn physics, there are several kinds of dipoles:*An electric dipole is a separation of positive and negative charges. The simplest example of this is a pair of electric charges of equal magnitude but opposite sign, separated by some distance. A permanent electric dipole is called an electret.*A...
- QuadrupoleQuadrupoleA quadrupole or quadrapole is one of a sequence of configurations of—for example—electric charge or current, or gravitational mass that can exist in ideal form, but it is usually just part of a multipole expansion of a more complex structure reflecting various orders of complexity.-Mathematical...
- Discrete dipole approximationDiscrete dipole approximationThe discrete dipole approximation is a method for computing scattering of radiation by particles of arbitrary shape and by periodic structures. Given a target of arbitrary geometry, one seeks to calculate its scattering and absorption properties...
- Magnetic dipole moment
- Bond dipole momentBond dipole momentThe bond dipole moment uses the idea of electric dipole moment to measure the polarity of a chemical bond within a molecule. The bond dipole μ is given by:\mu = \delta \, d....
- Neutron electric dipole momentNeutron electric dipole momentThe neutron electric dipole moment is a measure for the distribution of positive and negative charge inside the neutron. A finite electric dipole moment can only exist if the centers of the negative and positive charge distribution inside the particle do not coincide. So far, no neutron EDM has...
- Electron electric dipole momentElectron electric dipole momentThe electron electric dipole moment de is an intrinsic property of an electron such that the potential energy is linearly related to the strength of the electric field: U=de·E. Within the standard model of elementary particle physics, such a dipole is predicted to be non-zero but very small, at...
- Multipole expansionMultipole expansionA multipole expansion is a mathematical series representing a function that depends on angles — usually the two angles on a sphere. These series are useful because they can often be truncated, meaning that only the first few terms need to be retained for a good approximation to the original...
- Multipole momentsMultipole momentsIn mathematics, especially as applied to physics, multipole moments are the coefficients of a series expansion of a potential due to continuous or discrete sources . A multipole moment usually involves powers of the distance to the origin, as well as some angular dependence...
- Solid harmonics
- Axial multipole momentsAxial multipole momentsAxial multipole moments are a series expansionof the electric potential of acharge distribution localized close tothe origin along oneCartesian axis,denoted here as the z-axis...
- Cylindrical multipole momentsCylindrical multipole momentsCylindrical multipole moments are the coefficients in a series expansion of a potential that varies logarithmically with the distance to a source, i.e., as \ln \ R...
- Spherical multipole momentsSpherical multipole momentsSpherical multipole moments are the coefficients in a series expansionof a potential that varies inversely with the distance R to a source, i.e., as 1/R...
- Laplace expansionLaplace expansion (potential)In physics, the Laplace expansion of a 1/r - type potential is applied to expand Newton's gravitational potential or Coulomb's electrostatic potential. In quantum mechanical calculations on atoms the expansion is used in the evaluation of integrals of the interelectronic repulsion.The Laplace...
- Legendre polynomials