Renormalization
Encyclopedia
In quantum field theory
, the statistical mechanics
of fields, and the theory of self-similar
geometric structures, renormalization is any of a collection of techniques used to treat infinities
arising in calculated quantities.
When describing space and time as a continuum, certain statistical and quantum mechanical constructions are ill defined. To define them, the continuum limit has to be taken carefully.
Renormalization establishes a relationship between parameters in the theory, when the parameters describing large distance scales differ from the parameters describing small distances. Renormalization was first developed in quantum electrodynamics
(QED) to make sense of infinite
integrals in perturbation theory
. Initially viewed as a suspicious provisional procedure by some of its originators, renormalization eventually was embraced as an important and self-consistent tool in several fields of physics
and mathematics
.
The problem of infinities first arose in the classical electrodynamics of point particle
s in the 19th and early 20th century.
The mass of a charged particle should include the mass-energy in its electrostatic field (Electromagnetic mass
). Assume that the particle is a charged spherical shell of radius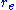
. The mass-energy in the field is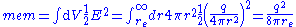
and it is infinite in the limit as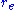
approaches zero, which implies that the point particle would have infinite inertia
, making it unable to be accelerated. Incidentally, the value of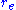
that makes 
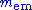equal to the electron mass is called the classical electron radius
, which (restoring factors of c and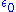
) turns out to be 
times smaller than the Compton wavelength
of the electron:
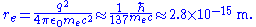
The total effective mass of a spherical charged particle includes the actual bare mass of the spherical shell (in addition to the aforementioned mass associated with its electric field). If the shell's bare mass is allowed to be negative, it might be possible to take a consistent point limit. This was called renormalization, and Lorentz
and Abraham
attempted to develop a classical theory of the electron this way. This early work was the inspiration for later attempts at regularization
and renormalization in quantum field theory.
When calculating the electromagnetic
interactions of charged
particles, it is tempting to ignore the back-reaction
of a particle's own field on itself. But this back reaction is necessary to explain the friction on charged particles when they emit radiation. If the electron is assumed to be a point, the value of the back-reaction diverges, for the same reason that the mass diverges, because the field is inverse-square
.
The Abraham–Lorentz theory had a noncausal "pre-acceleration". Sometimes an electron would start moving before the force is applied. This is a sign that the point limit is inconsistent. An extended body will start moving when a force is applied within one radius of the center of mass.
The trouble was worse in classical field theory than in quantum field theory, because in quantum field theory a charged particle experiences Zitterbewegung
due to interference with virtual particle-antiparticle pairs, thus effectively smearing out the charge over a region comparable to the Compton wavelength. In quantum electrodynamics at small coupling the electromagnetic mass only diverges as the log of the radius of the particle.
When developing quantum electrodynamics in the 1930s, Max Born
, Werner Heisenberg
, Pascual Jordan
, and Paul Dirac
discovered that in perturbative calculations many integrals were divergent.
One way of describing the divergences was discovered in the 1930s by Ernst Stueckelberg
, in the 1940s by Julian Schwinger
, Richard Feynman
, and Shin'ichiro Tomonaga, and systematized by Freeman Dyson
. The divergences appear in calculations involving Feynman diagram
s with closed loops of virtual particle
s in them.
While virtual particles obey conservation of energy
and momentum
, they can have any energy and momentum, even one that is not allowed by the relativistic energy-momentum relation for the observed mass of that particle. (That is,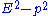
is not necessarily the mass of the particle in that process (e.g. for a photon it could be nonzero).) Such a particle is called off-shell. When there is a loop, the momentum of the particles involved in the loop is not uniquely determined by the energies and momenta of incoming and outgoing particles. A variation in the energy of one particle in the loop must be balanced by an equal and opposite variation in the energy of another particle in the loop. So to find the amplitude for the loop process one must integrate
over all possible combinations of energy and momentum that could travel around the loop.
These integrals are often divergent, that is, they give infinite answers. The divergences which are significant are the "ultraviolet
" (UV) ones. An ultraviolet divergence can be described as one which comes from
So these divergences are short-distance, short-time phenomena.
There are exactly three one-loop divergent loop diagrams in quantum electrodynamics.
The three divergences correspond to the three parameters in the theory:
A second class of divergence, called an infrared divergence
, is due to massless particles, like the photon. Every process involving charged particles emits infinitely many coherent photons of infinite wavelength, and the amplitude for emitting any finite number of photons is zero. For photons, these divergences are well understood. For example, at the 1-loop order, the vertex function has both ultraviolet and infrared divergences. In contrast to the ultraviolet divergence, the infrared divergence does not require the renormalization of a parameter in the theory. The infrared divergence of the vertex diagram is removed by including a diagram similar to the vertex diagram with the following important difference: the photon connecting the two legs of the electron is cut and replaced by two on shell (i.e. real) photons whose wavelengths tend to infinity; this diagram is equivalent to the bremsstrahlung
process. This additional diagram must be included because there is no physical way to distinguish a zero-energy photon flowing through a loop as in the vertex diagram and zero-energy photons emitted through bremsstrahlung
. From a mathematical point of view the IR divergences can be regularized by assuming fractional differentiation with respect to a parameter, for example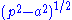
is well defined at p = a but is UV divergent, if we take the 3/2-th fractional derivative with respect to 
we obtain the IR divergence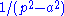 
so we can cure IR divergences by turning them into UV divergencies
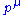and ends up with four-momentum 
. It emits a virtual photon carrying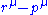 
to transfer energy and momentum to the other electron. But in this diagram, before that happens, it emits another virtual photon carrying four-momentum 
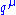, and it reabsorbs this one after emitting the other virtual photon. Energy and momentum conservation do not determine the four-momentum 
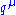uniquely, so all possibilities contribute equally and we must integrate.
This diagram's amplitude ends up with, among other things, a factor from the loop of
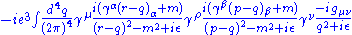
The various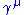
factors in this expression are gamma matrices as in the covariant formulation of the Dirac equation
; they have to do with the spin of the electron. The factors of
are the electric coupling constant, while the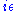 
provide a heuristic definition of the contour of integration around the poles in the space of momenta. The important part for our purposes is the dependency on 
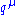of the three big factors in the integrand, which are from the propagator
s of the two electron lines and the photon line in the loop.
This has a piece with two powers of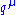
on top that dominates at large values of 
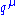(Pokorski 1987, p. 122):
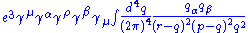
This integral is divergent, and infinite unless we cut it off at finite energy and momentum in some way.
Similar loop divergences occur in other quantum field theories.
), representing such things as the electron's electric charge
and mass
, as well as the normalizations of the quantum fields themselves, did not actually correspond to the physical constants measured in the laboratory. As written, they were bare quantities that did not take into account the contribution of virtual-particle loop effects to the physical constants themselves. Among other things, these effects would include the quantum counterpart of the electromagnetic back-reaction that so vexed classical theorists of electromagnetism. In general, these effects would be just as divergent as the amplitudes under study in the first place; so finite measured quantities would in general imply divergent bare quantities.
In order to make contact with reality, then, the formulae would have to be rewritten in terms of measurable, renormalized quantities. The charge of the electron, say, would be defined in terms of a quantity measured at a specific kinematic
renormalization point or subtraction point (which will generally have a characteristic energy, called the renormalization scale or simply the energy scale). The parts of the Lagrangian left over, involving the remaining portions of the bare quantities, could then be reinterpreted as counterterms, involved in divergent diagrams exactly canceling out the troublesome divergences for other diagrams.
For example, in the Lagrangian of QED
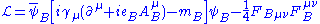
the fields and coupling constant are really bare quantities, hence the subscript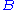
above. Conventionally the bare quantities are written so that the corresponding Lagrangian terms are multiples of the renormalized ones:
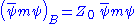
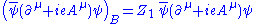
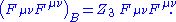
(Gauge invariance, via a Ward–Takahashi identity
, turns out to imply that we can renormalize the two terms of the covariant derivative
piece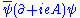
together (Pokorski 1987, p. 115), which is what happened to 
; it is the same as 
.)
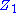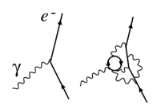
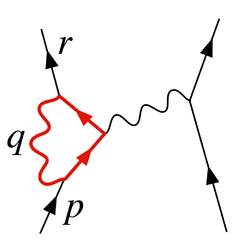
A term in this Lagrangian, for example, the electron-photon interaction pictured in Figure 1, can then be written
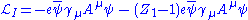
The physical constant
, the electron's charge, can then be defined in terms of some specific experiment; we set the renormalization scale equal to the energy characteristic of this experiment, and the first term gives the interaction we see in the laboratory (up to small, finite corrections from loop diagrams, providing such exotica as the high-order corrections to the magnetic moment
). The rest is the counterterm. If we are lucky, the divergent parts of loop diagrams can all be decomposed into pieces with three or fewer legs, with an algebraic form that can be canceled out by the second term (or by the similar counterterms that come from
and 
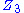). In QED, we are lucky: the theory is renormalizable (see below for more on this).
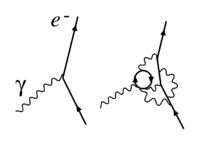
The diagram with the
counterterm's interaction vertex placed as in Figure 3 cancels out the divergence from the loop in Figure 2.
The splitting of the "bare terms" into the original terms and counterterms came before the renormalization group
insights due to Kenneth Wilson. According to the renormalization group
insights, this splitting is unnatural and unphysical.
with changes in scale. This variation is encoded by beta-function
s, and the general theory of this kind of scale-dependence is known as the renormalization group
.
Colloquially, particle physicists often speak of certain physical constants as varying with the energy of an interaction, though in fact it is the renormalization scale that is the independent quantity. This running does, however, provide a convenient means of describing changes in the behavior of a field theory under changes in the energies involved in an interaction. For example, since the coupling constant in quantum chromodynamics
becomes small at large energy scales, the theory behaves more like a free theory as the energy exchanged in an interaction becomes large, a phenomenon known as asymptotic freedom
. Choosing an increasing energy scale and using the renormalization group makes this clear from simple Feynman diagrams; were this not done, the prediction would be the same, but would arise from complicated high-order cancellations.
Take an example: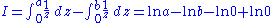
is ill defined.
To eliminate divergence, simply change lower limit of integral into
and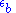 
:
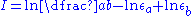
Make sure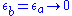
, then 
.
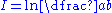is ill-defined, in order to make this notion of canceling divergences precise, the divergences first have to be tamed mathematically using the theory of limits
, in a process known as regularization
.
An essentially arbitrary modification to the loop integrands, or regulator, can make them drop off faster at high energies and momenta, in such a manner that the integrals converge. A regulator has a characteristic energy scale known as the cutoff
; taking this cutoff to infinity (or, equivalently, the corresponding length/time scale to zero) recovers the original integrals.
With the regulator in place, and a finite value for the cutoff, divergent terms in the integrals then turn into finite but cutoff-dependent terms. After canceling out these terms with the contributions from cutoff-dependent counterterms, the cutoff is taken to infinity and finite physical results recovered. If physics on scales we can measure is independent of what happens at the very shortest distance and time scales, then it should be possible to get cutoff-independent results for calculations.
Many different types of regulator are used in quantum field theory calculations, each with its advantages and disadvantages. One of the most popular in modern use is dimensional regularization
, invented by Gerardus 't Hooft
and Martinus J. G. Veltman
, which tames the integrals by carrying them into a space with a fictitious fractional number of dimensions. Another is Pauli–Villars regularization, which adds fictitious particles to the theory with very large masses, such that loop integrands involving the massive particles cancel out the existing loops at large momenta.
Yet another regularization scheme is the Lattice regularization, introduced by Kenneth Wilson, which pretends that our space-time is constructed by hyper-cubical lattice with fixed grid size. This size is a natural cutoff for the maximal momentum that a particle could possess when propagating on the lattice. And after doing calculation on several lattices with different grid size, the physical result is extrapolated to grid size 0, or our natural universe. This presupposes the existence of a scaling limit
.
A rigorous mathematical approach to renormalization theory is the so-called causal perturbation theory
, where ultraviolet divergences are avoided from the start in calculations by performing well-defined mathematical operations only within the framework of distribution
theory. The disadvantage of the method is the fact that the approach is quite technical and requires a high level of mathematical knowledge.
discovered a relationship between zeta function regularization
and renormalization, using the asymptotic relation:
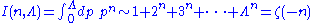
as the regulator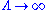
. Based on this, he considered using the values of 
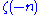to get finite results. Although he reached inconsistent results, an improved formula studied by Hartle
, J. Garcia, and E. Elizalde includes the technique of the zeta regularization algorithm
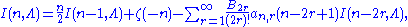
where the Bs are the Bernoulli number
s and
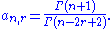
So every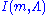
can be written as a linear combination of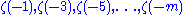 
Or simply using Abel–Plana formula we have for every divergent integral:
valid when m > 0, Here the zeta function is Hurwitz zeta function and Beta is a positive real number.
The "geometric" analogy is given by, (if we use rectangle method
) to evaluate the integral so:
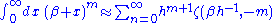
Using Hurwitz zeta regularization plus rectangle method with step h (not to be confused with Planck's constant)
For multi-loop integrals that will depend on several variables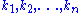
we can make a change of variables to polar coordinates and then replace the integral over the angles 
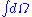by a sum so we have only a divergent integral , that will depend on the modulus 
and then we can apply the zeta regularization algorithm, the main idea for multi-loop integrals is to replace the factor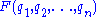 
after a change to hyperspherical coordinates 
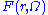so the UV overlapping divergences are encoded in variable r. In order toregularize these integrals one needs a regulator, for the case of multi-loop integrals, these regulator can be taken as 
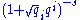so the multi-loop integral will converge for big enough 's' using the Zeta regularization we can analytic continue the variable 's' to the physical limit where s=0 and then regularize any UV integral.
Dirac
's criticism was the most persistent. As late as 1975, he was saying:
Another important critic was Feynman
. Despite his crucial role in the development of quantum electrodynamics, he wrote the following in 1985:
While Dirac's criticism was based on the procedure of renormalization itself, Feynman's criticism was very different. Feynman was concerned that all field theories known in the 1960s had the property that the interactions become infinitely strong at short enough distance scales. This property, called a Landau pole
, made it plausible that quantum field theories were all inconsistent. In 1974, Gross
, Politzer and Wilczek
showed that another quantum field theory, quantum chromodynamics
, does not have a Landau pole. Feynman, along with most others, accepted that QCD was a fully consistent theory.
The general unease was almost universal in texts up to the 1970s and 1980s. Beginning in the 1970s, however, inspired by work on the renormalization group
and effective field theory
, and despite the fact that Dirac and various others—all of whom belonged to the older generation—never withdrew their criticisms, attitudes began to change, especially among younger theorists. Kenneth G. Wilson
and others demonstrated that the renormalization group is useful in statistical
field theory applied to condensed matter physics
, where it provides important insights into the behavior of phase transition
s. In condensed matter physics, a real short-distance regulator exists: matter
ceases to be continuous on the scale of atom
s. Short-distance divergences in condensed matter physics do not present a philosophical problem, since the field theory is only an effective, smoothed-out representation of the behavior of matter anyway; there are no infinities since the cutoff is actually always finite, and it makes perfect sense that the bare quantities are cutoff-dependent.
If QFT
holds all the way down past the Planck length (where it might yield to string theory
, causal set theory or something different), then there may be no real problem with short-distance divergences in particle physics
either; all field theories could simply be effective field theories. In a sense, this approach echoes the older attitude that the divergences in QFT speak of human ignorance about the workings of nature, but also acknowledges that this ignorance can be quantified and that the resulting effective theories remain useful.
In QFT, the value of a physical constant, in general, depends on the scale that one chooses as the renormalization point, and it becomes very interesting to examine the renormalization group running of physical constants under changes in the energy scale. The coupling constants in the Standard Model
of particle physics vary in different ways with increasing energy scale: the coupling of quantum chromodynamics
and the weak isospin coupling of the electroweak force tend to decrease, and the weak hypercharge coupling of the electroweak force tends to increase. At the colossal energy scale of 1015 GeV
(far beyond the reach of our current particle accelerator
s), they all become approximately the same size (Grotz and Klapdor 1990, p. 254), a major motivation for speculations about grand unified theory. Instead of being only a worrisome problem, renormalization has become an important theoretical tool for studying the behavior of field theories in different regimes.
If a theory featuring renormalization (e.g. QED) can only be sensibly interpreted as an effective field theory, i.e. as an approximation reflecting human ignorance about the workings of nature, then the problem remains of discovering a more accurate theory that does not have these renormalization problems. As Lewis Ryder has put it, "In the Quantum Theory, these [classical] divergences do not disappear; on the contrary, they appear to get worse. And despite the comparative success of renormalisation theory the feeling remains that there ought to be a more satisfactory way of doing things."
in energy units, the counterterms required to cancel all divergences proliferate to infinite number, and, at first glance, the theory would seem to gain an infinite number of free parameters and therefore lose all predictive power, becoming scientifically worthless. Such theories are called nonrenormalizable.
The Standard Model
of particle physics contains only renormalizable operators, but the interactions of general relativity
become nonrenormalizable operators if one attempts to construct a field theory of quantum gravity
in the most straightforward manner, suggesting that perturbation theory
is useless in application to quantum gravity.
However, in an effective field theory
, "renormalizability" is, strictly speaking, a misnomer
. In a nonrenormalizable effective field theory, terms in the Lagrangian do multiply to infinity, but have coefficients suppressed by ever-more-extreme inverse powers of the energy cutoff. If the cutoff is a real, physical quantity—if, that is, the theory is only an effective description of physics up to some maximum energy or minimum distance scale—then these extra terms could represent real physical interactions. Assuming that the dimensionless constants in the theory do not get too large, one can group calculations by inverse powers of the cutoff, and extract approximate predictions to finite order in the cutoff that still have a finite number of free parameters. It can even be useful to renormalize these "nonrenormalizable" interactions.
Nonrenormalizable interactions in effective field theories rapidly become weaker as the energy scale becomes much smaller than the cutoff. The classic example is the Fermi theory
of the weak nuclear force, a nonrenormalizable effective theory whose cutoff is comparable to the mass of the W particle. This fact may also provide a possible explanation for why almost all of the particle interactions we see are describable by renormalizable theories. It may be that any others that may exist at the GUT or Planck scale simply become too weak to detect in the realm we can observe, with one exception: gravity, whose exceedingly weak interaction is magnified by the presence of the enormous masses of star
s and planet
s.
, namely to the problems of the critical behaviour near second-order phase transitions, in particular at fictitious spatial dimensions just below the number of 4, where the above-mentioned methods could even be sharpened (i.e., instead of "renormalizability" one gets "super-renormalizability"), which allowed extrapolation to the real spatial dimensionality for phase transitions, 3. Details can be found in the book of Zinn-Justin, mentioned below.
For the discovery of these unexpected applications, and working out the details, in 1982 the physics Nobel prize was awarded to Kenneth G. Wilson
.
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, the statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
of fields, and the theory of self-similar
Self-similarity
In mathematics, a self-similar object is exactly or approximately similar to a part of itself . Many objects in the real world, such as coastlines, are statistically self-similar: parts of them show the same statistical properties at many scales...
geometric structures, renormalization is any of a collection of techniques used to treat infinities
Infinity
Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
arising in calculated quantities.
When describing space and time as a continuum, certain statistical and quantum mechanical constructions are ill defined. To define them, the continuum limit has to be taken carefully.
Renormalization establishes a relationship between parameters in the theory, when the parameters describing large distance scales differ from the parameters describing small distances. Renormalization was first developed in quantum electrodynamics
Quantum electrodynamics
Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
(QED) to make sense of infinite
Infinity
Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
integrals in perturbation theory
Perturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
. Initially viewed as a suspicious provisional procedure by some of its originators, renormalization eventually was embraced as an important and self-consistent tool in several fields of physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
.
Self-interactions in classical physics
Elementary particle
In particle physics, an elementary particle or fundamental particle is a particle not known to have substructure; that is, it is not known to be made up of smaller particles. If an elementary particle truly has no substructure, then it is one of the basic building blocks of the universe from which...
s in the 19th and early 20th century.
The mass of a charged particle should include the mass-energy in its electrostatic field (Electromagnetic mass
Electromagnetic mass
Electromagnetic mass was initially a concept of classical mechanics, denoting as to how much the electromagnetic field, or the self-energy, is contributing to the mass of charged particles. It was first derived by J. J. Thomson in 1881 and was for some time also considered as a dynamical...
). Assume that the particle is a charged spherical shell of radius
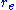. The mass-energy in the field is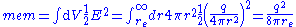and it is infinite in the limit as
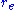approaches zero, which implies that the point particle would have infinite inertiaInertia
Inertia is the resistance of any physical object to a change in its state of motion or rest, or the tendency of an object to resist any change in its motion. It is proportional to an object's mass. The principle of inertia is one of the fundamental principles of classical physics which are used to...
, making it unable to be accelerated. Incidentally, the value of
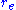that makes 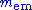equal to the electron mass is called the classical electron radiusClassical electron radius
The classical electron radius, also known as the Lorentz radius or the Thomson scattering length, is based on a classical relativistic model of the electron...
, which (restoring factors of c and
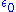) turns out to be times smaller than the Compton wavelengthCompton wavelength
The Compton wavelength is a quantum mechanical property of a particle. It was introduced by Arthur Compton in his explanation of the scattering of photons by electrons...
of the electron:
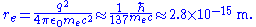
The total effective mass of a spherical charged particle includes the actual bare mass of the spherical shell (in addition to the aforementioned mass associated with its electric field). If the shell's bare mass is allowed to be negative, it might be possible to take a consistent point limit. This was called renormalization, and Lorentz
Lorentz
Lorentz is a name derived from the Roman surname, Laurentius, which mean "from Laurentum". It is the German form of Laurence.Lorentz may refer to:- Literature :* Friedrich Lorentz, author of works on the Pomeranian language...
and Abraham
Max Abraham
Max Abraham was a German physicist.Abraham was born in Danzig, Imperial Germany to a family of Jewish merchants. His father was Moritz Abraham and his mother was Selma Moritzsohn. Attending the University of Berlin, he studied under Max Planck. He graduated in 1897...
attempted to develop a classical theory of the electron this way. This early work was the inspiration for later attempts at regularization
Regularization (physics)
-Introduction:In physics, especially quantum field theory, regularization is a method of dealing with infinite, divergent, and non-sensical expressions by introducing an auxiliary concept of a regulator...
and renormalization in quantum field theory.
When calculating the electromagnetic
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
interactions of charged
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
particles, it is tempting to ignore the back-reaction
Back-reaction
In theoretical physics, Back-reaction is often necessary to calculate the behavior of a particle or an object in an external field.When the particle is considered to be infinitely light or have an infinitesimal charge, it is said that we deal with a probe and the back-reaction is neglected...
of a particle's own field on itself. But this back reaction is necessary to explain the friction on charged particles when they emit radiation. If the electron is assumed to be a point, the value of the back-reaction diverges, for the same reason that the mass diverges, because the field is inverse-square
Inverse-square law
In physics, an inverse-square law is any physical law stating that a specified physical quantity or strength is inversely proportional to the square of the distance from the source of that physical quantity....
.
The Abraham–Lorentz theory had a noncausal "pre-acceleration". Sometimes an electron would start moving before the force is applied. This is a sign that the point limit is inconsistent. An extended body will start moving when a force is applied within one radius of the center of mass.
The trouble was worse in classical field theory than in quantum field theory, because in quantum field theory a charged particle experiences Zitterbewegung
Zitterbewegung
Zitterbewegung is a theoretical rapid motion of elementary particles, in particular electrons, that obey the Dirac equation...
due to interference with virtual particle-antiparticle pairs, thus effectively smearing out the charge over a region comparable to the Compton wavelength. In quantum electrodynamics at small coupling the electromagnetic mass only diverges as the log of the radius of the particle.
Divergences in quantum electrodynamics
Max Born
Max Born was a German-born physicist and mathematician who was instrumental in the development of quantum mechanics. He also made contributions to solid-state physics and optics and supervised the work of a number of notable physicists in the 1920s and 30s...
, Werner Heisenberg
Werner Heisenberg
Werner Karl Heisenberg was a German theoretical physicist who made foundational contributions to quantum mechanics and is best known for asserting the uncertainty principle of quantum theory...
, Pascual Jordan
Pascual Jordan
-Further reading:...
, and Paul Dirac
Paul Dirac
Paul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
discovered that in perturbative calculations many integrals were divergent.
One way of describing the divergences was discovered in the 1930s by Ernst Stueckelberg
Ernst Stueckelberg
Ernst Carl Gerlach Stueckelberg was a Swiss mathematician and physicist.- Career :In 1927 Stueckelberg got his Ph. D. at the University of Basel under August Hagenbach...
, in the 1940s by Julian Schwinger
Julian Schwinger
Julian Seymour Schwinger was an American theoretical physicist. He is best known for his work on the theory of quantum electrodynamics, in particular for developing a relativistically invariant perturbation theory, and for renormalizing QED to one loop order.Schwinger is recognized as one of the...
, Richard Feynman
Richard Feynman
Richard Phillips Feynman was an American physicist known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics and the physics of the superfluidity of supercooled liquid helium, as well as in particle physics...
, and Shin'ichiro Tomonaga, and systematized by Freeman Dyson
Freeman Dyson
Freeman John Dyson FRS is a British-born American theoretical physicist and mathematician, famous for his work in quantum field theory, solid-state physics, astronomy and nuclear engineering. Dyson is a member of the Board of Sponsors of the Bulletin of the Atomic Scientists...
. The divergences appear in calculations involving Feynman diagram
Feynman diagram
Feynman diagrams are a pictorial representation scheme for the mathematical expressions governing the behavior of subatomic particles, first developed by the Nobel Prize-winning American physicist Richard Feynman, and first introduced in 1948...
s with closed loops of virtual particle
Virtual particle
In physics, a virtual particle is a particle that exists for a limited time and space. The energy and momentum of a virtual particle are uncertain according to the uncertainty principle...
s in them.
While virtual particles obey conservation of energy
Conservation of energy
The nineteenth century law of conservation of energy is a law of physics. It states that the total amount of energy in an isolated system remains constant over time. The total energy is said to be conserved over time...
and momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
, they can have any energy and momentum, even one that is not allowed by the relativistic energy-momentum relation for the observed mass of that particle. (That is,
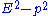is not necessarily the mass of the particle in that process (e.g. for a photon it could be nonzero).) Such a particle is called off-shell. When there is a loop, the momentum of the particles involved in the loop is not uniquely determined by the energies and momenta of incoming and outgoing particles. A variation in the energy of one particle in the loop must be balanced by an equal and opposite variation in the energy of another particle in the loop. So to find the amplitude for the loop process one must integrateIntegral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
over all possible combinations of energy and momentum that could travel around the loop.
These integrals are often divergent, that is, they give infinite answers. The divergences which are significant are the "ultraviolet
Ultraviolet divergence
In physics, an ultraviolet divergence is a situation in which an integral, for example a Feynman diagram, diverges because of contributions of objects with very high energy , or, equivalently, because of physical phenomena at very short distances. An infinite answer to a question that should have a...
" (UV) ones. An ultraviolet divergence can be described as one which comes from
- the region in the integral where all particles in the loop have large energies and momenta.
- very short wavelengthWavelengthIn physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
s and high frequenciesFrequencyFrequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
fluctuations of the fields, in the path integralPath integral formulationThe path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics...
for the field. - Very short proper-time between particle emission and absorption, if the loop is thought of as a sum over particle paths.
So these divergences are short-distance, short-time phenomena.
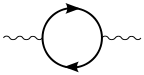
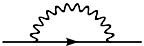
There are exactly three one-loop divergent loop diagrams in quantum electrodynamics.
- a photon creates a virtual electron-positronPositronThe positron or antielectron is the antiparticle or the antimatter counterpart of the electron. The positron has an electric charge of +1e, a spin of ½, and has the same mass as an electron...
pair which then annihilate, this is a vacuum polarization diagram. - an electron which quickly emits and reabsorbs a virtual photon, called a self-energy.
- An electron emits a photon, emits a second photon, and reabsorbs the first. This process is shown in figure 2, and it is called a vertex renormalization. The Feynman diagram for this is also called a penguin diagramPenguin diagramIn quantum field theory, penguin diagrams are a class of Feynman diagrams which are important for understanding CP violating processes in the standard model. They refer to one-loop processes in which a quark temporarily changes flavor , and the flavor-changed quark engages in some tree interaction,...
due to its shape remotely resembling a penguin (with the initial and final state electrons as the arms and legs, the second photon as the body and the first looping photon as the head).
The three divergences correspond to the three parameters in the theory:
- the field normalization Z.
- the mass of the electron.
- the charge of the electron.
A second class of divergence, called an infrared divergence
Infrared divergence
In physics, an infrared divergence or infrared catastrophe is a situation in which an integral, for example a Feynman diagram, diverges because of contributions of objects with very small energy approaching zero, or, equivalently, because of physical phenomena at very long distances.The infrared ...
, is due to massless particles, like the photon. Every process involving charged particles emits infinitely many coherent photons of infinite wavelength, and the amplitude for emitting any finite number of photons is zero. For photons, these divergences are well understood. For example, at the 1-loop order, the vertex function has both ultraviolet and infrared divergences. In contrast to the ultraviolet divergence, the infrared divergence does not require the renormalization of a parameter in the theory. The infrared divergence of the vertex diagram is removed by including a diagram similar to the vertex diagram with the following important difference: the photon connecting the two legs of the electron is cut and replaced by two on shell (i.e. real) photons whose wavelengths tend to infinity; this diagram is equivalent to the bremsstrahlung
Bremsstrahlung
Bremsstrahlung is electromagnetic radiation produced by the deceleration of a charged particle when deflected by another charged particle, typically an electron by an atomic nucleus. The moving particle loses kinetic energy, which is converted into a photon because energy is conserved. The term is...
process. This additional diagram must be included because there is no physical way to distinguish a zero-energy photon flowing through a loop as in the vertex diagram and zero-energy photons emitted through bremsstrahlung
Bremsstrahlung
Bremsstrahlung is electromagnetic radiation produced by the deceleration of a charged particle when deflected by another charged particle, typically an electron by an atomic nucleus. The moving particle loses kinetic energy, which is converted into a photon because energy is conserved. The term is...
. From a mathematical point of view the IR divergences can be regularized by assuming fractional differentiation with respect to a parameter, for example
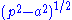is well defined at p = a but is UV divergent, if we take the 3/2-th fractional derivative with respect to we obtain the IR divergence 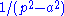so we can cure IR divergences by turning them into UV divergenciesA loop divergence
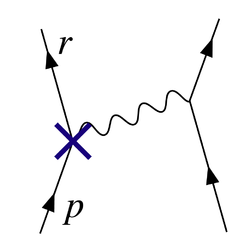
The diagram in Figure 2 shows one of the several one-loop contributions to electron-electron scattering in QED. The electron on the left side of the diagram, represented by the solid line, starts out with four-momentum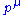 and ends up with four-momentum . It emits a virtual photon carrying 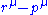to transfer energy and momentum to the other electron. But in this diagram, before that happens, it emits another virtual photon carrying four-momentum 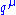, and it reabsorbs this one after emitting the other virtual photon. Energy and momentum conservation do not determine the four-momentum 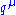uniquely, so all possibilities contribute equally and we must integrate.This diagram's amplitude ends up with, among other things, a factor from the loop of
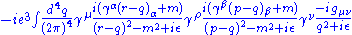
The various
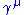factors in this expression are gamma matrices as in the covariant formulation of the Dirac equationDirac equation
The Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and...
; they have to do with the spin of the electron. The factors of
are the electric coupling constant, while the 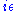provide a heuristic definition of the contour of integration around the poles in the space of momenta. The important part for our purposes is the dependency on 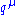of the three big factors in the integrand, which are from the propagatorPropagator
In quantum mechanics and quantum field theory, the propagator gives the probability amplitude for a particle to travel from one place to another in a given time, or to travel with a certain energy and momentum. Propagators are used to represent the contribution of virtual particles on the internal...
s of the two electron lines and the photon line in the loop.
This has a piece with two powers of
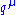on top that dominates at large values of 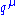(Pokorski 1987, p. 122):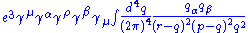This integral is divergent, and infinite unless we cut it off at finite energy and momentum in some way.
Similar loop divergences occur in other quantum field theories.
Renormalized and bare quantities
The solution was to realize that the quantities initially appearing in the theory's formulae (such as the formula for the LagrangianLagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
), representing such things as the electron's electric charge
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
and mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
, as well as the normalizations of the quantum fields themselves, did not actually correspond to the physical constants measured in the laboratory. As written, they were bare quantities that did not take into account the contribution of virtual-particle loop effects to the physical constants themselves. Among other things, these effects would include the quantum counterpart of the electromagnetic back-reaction that so vexed classical theorists of electromagnetism. In general, these effects would be just as divergent as the amplitudes under study in the first place; so finite measured quantities would in general imply divergent bare quantities.
In order to make contact with reality, then, the formulae would have to be rewritten in terms of measurable, renormalized quantities. The charge of the electron, say, would be defined in terms of a quantity measured at a specific kinematic
Kinematics
Kinematics is the branch of classical mechanics that describes the motion of bodies and systems without consideration of the forces that cause the motion....
renormalization point or subtraction point (which will generally have a characteristic energy, called the renormalization scale or simply the energy scale). The parts of the Lagrangian left over, involving the remaining portions of the bare quantities, could then be reinterpreted as counterterms, involved in divergent diagrams exactly canceling out the troublesome divergences for other diagrams.
Renormalization in QED
Quantum electrodynamics
Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
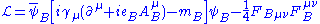
the fields and coupling constant are really bare quantities, hence the subscript
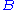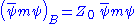
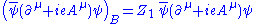
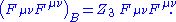
above. Conventionally the bare quantities are written so that the corresponding Lagrangian terms are multiples of the renormalized ones:(Gauge invariance, via a Ward–Takahashi identity
Ward–Takahashi identity
In quantum field theory, a Ward-Takahashi identity is an identity between correlation functions that follows from the global or gauged symmetries of the theory, and which remains valid after renormalization....
, turns out to imply that we can renormalize the two terms of the covariant derivative
Covariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
piece
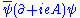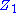together (Pokorski 1987, p. 115), which is what happened to ; it is the same as .)A term in this Lagrangian, for example, the electron-photon interaction pictured in Figure 1, can then be written
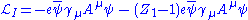
The physical constant
, the electron's charge, can then be defined in terms of some specific experiment; we set the renormalization scale equal to the energy characteristic of this experiment, and the first term gives the interaction we see in the laboratory (up to small, finite corrections from loop diagrams, providing such exotica as the high-order corrections to the magnetic momentMagnetic moment
The magnetic moment of a magnet is a quantity that determines the force that the magnet can exert on electric currents and the torque that a magnetic field will exert on it...
). The rest is the counterterm. If we are lucky, the divergent parts of loop diagrams can all be decomposed into pieces with three or fewer legs, with an algebraic form that can be canceled out by the second term (or by the similar counterterms that come from
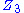and ). In QED, we are lucky: the theory is renormalizable (see below for more on this).The diagram with the
counterterm's interaction vertex placed as in Figure 3 cancels out the divergence from the loop in Figure 2.The splitting of the "bare terms" into the original terms and counterterms came before the renormalization group
Renormalization group
In theoretical physics, the renormalization group refers to a mathematical apparatus that allows systematic investigation of the changes of a physical system as viewed at different distance scales...
insights due to Kenneth Wilson. According to the renormalization group
Renormalization group
In theoretical physics, the renormalization group refers to a mathematical apparatus that allows systematic investigation of the changes of a physical system as viewed at different distance scales...
insights, this splitting is unnatural and unphysical.
Running constants
To minimize the contribution of loop diagrams to a given calculation (and therefore make it easier to extract results), one chooses a renormalization point close to the energies and momenta actually exchanged in the interaction. However, the renormalization point is not itself a physical quantity: the physical predictions of the theory, calculated to all orders, should in principle be independent of the choice of renormalization point, as long as it is within the domain of application of the theory. Changes in renormalization scale will simply affect how much of a result comes from Feynman diagrams without loops, and how much comes from the leftover finite parts of loop diagrams. One can exploit this fact to calculate the effective variation of physical constantsCoupling constant
In physics, a coupling constant, usually denoted g, is a number that determines the strength of an interaction. Usually the Lagrangian or the Hamiltonian of a system can be separated into a kinetic part and an interaction part...
with changes in scale. This variation is encoded by beta-function
Beta-function
In theoretical physics, specifically quantum field theory, a beta function β encodes the dependence of a coupling parameter, g, on the energy scale, \mu of a given physical process....
s, and the general theory of this kind of scale-dependence is known as the renormalization group
Renormalization group
In theoretical physics, the renormalization group refers to a mathematical apparatus that allows systematic investigation of the changes of a physical system as viewed at different distance scales...
.
Colloquially, particle physicists often speak of certain physical constants as varying with the energy of an interaction, though in fact it is the renormalization scale that is the independent quantity. This running does, however, provide a convenient means of describing changes in the behavior of a field theory under changes in the energies involved in an interaction. For example, since the coupling constant in quantum chromodynamics
Quantum chromodynamics
In theoretical physics, quantum chromodynamics is a theory of the strong interaction , a fundamental force describing the interactions of the quarks and gluons making up hadrons . It is the study of the SU Yang–Mills theory of color-charged fermions...
becomes small at large energy scales, the theory behaves more like a free theory as the energy exchanged in an interaction becomes large, a phenomenon known as asymptotic freedom
Asymptotic freedom
In physics, asymptotic freedom is a property of some gauge theories that causes interactions between particles to become arbitrarily weak at energy scales that become arbitrarily large, or, equivalently, at length scales that become arbitrarily small .Asymptotic freedom is a feature of quantum...
. Choosing an increasing energy scale and using the renormalization group makes this clear from simple Feynman diagrams; were this not done, the prediction would be the same, but would arise from complicated high-order cancellations.
Take an example:
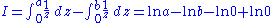is ill defined.To eliminate divergence, simply change lower limit of integral into
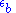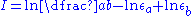
and :Make sure
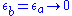, then 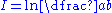.Regularization
Since the quantity is ill-defined, in order to make this notion of canceling divergences precise, the divergences first have to be tamed mathematically using the theory of limitsLimit (mathematics)
In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
, in a process known as regularization
Regularization (physics)
-Introduction:In physics, especially quantum field theory, regularization is a method of dealing with infinite, divergent, and non-sensical expressions by introducing an auxiliary concept of a regulator...
.
An essentially arbitrary modification to the loop integrands, or regulator, can make them drop off faster at high energies and momenta, in such a manner that the integrals converge. A regulator has a characteristic energy scale known as the cutoff
Cutoff
In theoretical physics, cutoff is an arbitrary maximal or minimal value of energy, momentum, or length, used in order that objects with larger or smaller values than these physical quantities are ignored in some calculation...
; taking this cutoff to infinity (or, equivalently, the corresponding length/time scale to zero) recovers the original integrals.
With the regulator in place, and a finite value for the cutoff, divergent terms in the integrals then turn into finite but cutoff-dependent terms. After canceling out these terms with the contributions from cutoff-dependent counterterms, the cutoff is taken to infinity and finite physical results recovered. If physics on scales we can measure is independent of what happens at the very shortest distance and time scales, then it should be possible to get cutoff-independent results for calculations.
Many different types of regulator are used in quantum field theory calculations, each with its advantages and disadvantages. One of the most popular in modern use is dimensional regularization
Dimensional regularization
In theoretical physics, dimensional regularization is a method introduced by Giambiagi and Bollini for regularizing integrals in the evaluation of Feynman diagrams; in other words, assigning values to them that are meromorphic functions of an auxiliary complex parameter d, called the...
, invented by Gerardus 't Hooft
Gerardus 't Hooft
Gerardus 't Hooft is a Dutch theoretical physicist and professor at Utrecht University, the Netherlands. He shared the 1999 Nobel Prize in Physics with his thesis advisor Martinus J. G...
and Martinus J. G. Veltman
Martinus J. G. Veltman
Martinus Justinus Godefriedus Veltman is a Dutch theoretical physicist. He shared the 1999 Nobel Prize in physics with his former student Gerardus 't Hooft for their work on particle theory.-Biography:...
, which tames the integrals by carrying them into a space with a fictitious fractional number of dimensions. Another is Pauli–Villars regularization, which adds fictitious particles to the theory with very large masses, such that loop integrands involving the massive particles cancel out the existing loops at large momenta.
Yet another regularization scheme is the Lattice regularization, introduced by Kenneth Wilson, which pretends that our space-time is constructed by hyper-cubical lattice with fixed grid size. This size is a natural cutoff for the maximal momentum that a particle could possess when propagating on the lattice. And after doing calculation on several lattices with different grid size, the physical result is extrapolated to grid size 0, or our natural universe. This presupposes the existence of a scaling limit
Scaling limit
In physics or mathematics, the scaling limit is a term applied to the behaviour of a lattice model in the limit of the lattice spacing going to zero. A lattice model which approximates a continuum quantum field theory in the limit as the lattice spacing goes to zero corresponds to finding a second...
.
A rigorous mathematical approach to renormalization theory is the so-called causal perturbation theory
Causal perturbation theory
Causal perturbation theory is a mathematically rigorous approach to renormalization theory, which makesit possible to put the theoretical setup of perturbative quantum field theory on a sound mathematical basis....
, where ultraviolet divergences are avoided from the start in calculations by performing well-defined mathematical operations only within the framework of distribution
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
theory. The disadvantage of the method is the fact that the approach is quite technical and requires a high level of mathematical knowledge.
Zeta function regularization
Julian SchwingerJulian Schwinger
Julian Seymour Schwinger was an American theoretical physicist. He is best known for his work on the theory of quantum electrodynamics, in particular for developing a relativistically invariant perturbation theory, and for renormalizing QED to one loop order.Schwinger is recognized as one of the...
discovered a relationship between zeta function regularization
Zeta function regularization
In mathematics and theoretical physics, zeta function regularization is a type of regularization or summability method that assigns finite values to divergent sums or products, and in particular can be used to define determinants and traces of some self-adjoint operators...
and renormalization, using the asymptotic relation:
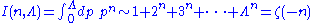
as the regulator
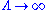. Based on this, he considered using the values of 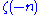to get finite results. Although he reached inconsistent results, an improved formula studied by HartleHartle
Hartle may refer to:*James Hartle, American physicist*Roy Hartle, retired soccer player...
, J. Garcia, and E. Elizalde includes the technique of the zeta regularization algorithm
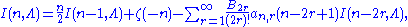
where the Bs are the Bernoulli number
Bernoulli number
In mathematics, the Bernoulli numbers Bn are a sequence of rational numbers with deep connections to number theory. They are closely related to the values of the Riemann zeta function at negative integers....
s and
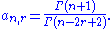
So every
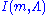can be written as a linear combination of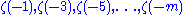 Or simply using Abel–Plana formula we have for every divergent integral:
valid when m > 0, Here the zeta function is Hurwitz zeta function and Beta is a positive real number.The "geometric" analogy is given by, (if we use rectangle method
Rectangle method
In mathematics, specifically in integral calculus, the rectangle method computes an approximation to a definite integral, made by finding the area of a collection of rectangles whose heights are determined by the values of the function.Specifically, the interval over which the function is to be...
) to evaluate the integral so:
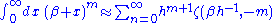
Using Hurwitz zeta regularization plus rectangle method with step h (not to be confused with Planck's constant)
For multi-loop integrals that will depend on several variables
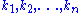we can make a change of variables to polar coordinates and then replace the integral over the angles 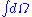by a sum so we have only a divergent integral , that will depend on the modulus and then we can apply the zeta regularization algorithm, the main idea for multi-loop integrals is to replace the factor 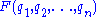after a change to hyperspherical coordinates 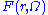so the UV overlapping divergences are encoded in variable r. In order toregularize these integrals one needs a regulator, for the case of multi-loop integrals, these regulator can be taken as 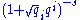so the multi-loop integral will converge for big enough 's' using the Zeta regularization we can analytic continue the variable 's' to the physical limit where s=0 and then regularize any UV integral.Attitudes and interpretation
The early formulators of QED and other quantum field theories were, as a rule, dissatisfied with this state of affairs. It seemed illegitimate to do something tantamount to subtracting infinities from infinities to get finite answers.Dirac
Paul Dirac
Paul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
's criticism was the most persistent. As late as 1975, he was saying:
- Most physicists are very satisfied with the situation. They say: 'Quantum electrodynamics is a good theory and we do not have to worry about it any more.' I must say that I am very dissatisfied with the situation, because this so-called 'good theory' does involve neglecting infinities which appear in its equations, neglecting them in an arbitrary way. This is just not sensible mathematics. Sensible mathematics involves neglecting a quantity when it is small - not neglecting it just because it is infinitely great and you do not want it!
Another important critic was Feynman
Richard Feynman
Richard Phillips Feynman was an American physicist known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics and the physics of the superfluidity of supercooled liquid helium, as well as in particle physics...
. Despite his crucial role in the development of quantum electrodynamics, he wrote the following in 1985:
- The shell game that we play ... is technically called 'renormalization'. But no matter how clever the word, it is still what I would call a dippy process! Having to resort to such hocus-pocus has prevented us from proving that the theory of quantum electrodynamics is mathematically self-consistent. It's surprising that the theory still hasn't been proved self-consistent one way or the other by now; I suspect that renormalization is not mathematically legitimate.
While Dirac's criticism was based on the procedure of renormalization itself, Feynman's criticism was very different. Feynman was concerned that all field theories known in the 1960s had the property that the interactions become infinitely strong at short enough distance scales. This property, called a Landau pole
Landau pole
In physics, the Landau pole is the momentum scale at which the coupling constant of a quantum field theory becomes infinite...
, made it plausible that quantum field theories were all inconsistent. In 1974, Gross
David Gross
David Jonathan Gross is an American particle physicist and string theorist. Along with Frank Wilczek and David Politzer, he was awarded the 2004 Nobel Prize in Physics for their discovery of asymptotic freedom. He is currently the director and holder of the Frederick W...
, Politzer and Wilczek
Frank Wilczek
Frank Anthony Wilczek is a theoretical physicist from the United States and a Nobel laureate. He is currently the Herman Feshbach Professor of Physics at the Massachusetts Institute of Technology ....
showed that another quantum field theory, quantum chromodynamics
Quantum chromodynamics
In theoretical physics, quantum chromodynamics is a theory of the strong interaction , a fundamental force describing the interactions of the quarks and gluons making up hadrons . It is the study of the SU Yang–Mills theory of color-charged fermions...
, does not have a Landau pole. Feynman, along with most others, accepted that QCD was a fully consistent theory.
The general unease was almost universal in texts up to the 1970s and 1980s. Beginning in the 1970s, however, inspired by work on the renormalization group
Renormalization group
In theoretical physics, the renormalization group refers to a mathematical apparatus that allows systematic investigation of the changes of a physical system as viewed at different distance scales...
and effective field theory
Effective field theory
In physics, an effective field theory is, as any effective theory, an approximate theory, that includes appropriate degrees of freedom to describe physical phenomena occurring at a chosen length scale, while ignoring substructure and degrees of freedom at shorter distances .-The renormalization...
, and despite the fact that Dirac and various others—all of whom belonged to the older generation—never withdrew their criticisms, attitudes began to change, especially among younger theorists. Kenneth G. Wilson
Kenneth G. Wilson
Kenneth Geddes Wilson is an American theoretical physicist and Nobel Prize winner.As an undergraduate at Harvard, he was a Putnam Fellow. He earned his PhD from Caltech in 1961, studying under Murray Gell-Mann....
and others demonstrated that the renormalization group is useful in statistical
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
field theory applied to condensed matter physics
Condensed matter physics
Condensed matter physics deals with the physical properties of condensed phases of matter. These properties appear when a number of atoms at the supramolecular and macromolecular scale interact strongly and adhere to each other or are otherwise highly concentrated in a system. The most familiar...
, where it provides important insights into the behavior of phase transition
Phase transition
A phase transition is the transformation of a thermodynamic system from one phase or state of matter to another.A phase of a thermodynamic system and the states of matter have uniform physical properties....
s. In condensed matter physics, a real short-distance regulator exists: matter
Matter
Matter is a general term for the substance of which all physical objects consist. Typically, matter includes atoms and other particles which have mass. A common way of defining matter is as anything that has mass and occupies volume...
ceases to be continuous on the scale of atom
Atom
The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...
s. Short-distance divergences in condensed matter physics do not present a philosophical problem, since the field theory is only an effective, smoothed-out representation of the behavior of matter anyway; there are no infinities since the cutoff is actually always finite, and it makes perfect sense that the bare quantities are cutoff-dependent.
If QFT
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
holds all the way down past the Planck length (where it might yield to string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
, causal set theory or something different), then there may be no real problem with short-distance divergences in particle physics
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
either; all field theories could simply be effective field theories. In a sense, this approach echoes the older attitude that the divergences in QFT speak of human ignorance about the workings of nature, but also acknowledges that this ignorance can be quantified and that the resulting effective theories remain useful.
In QFT, the value of a physical constant, in general, depends on the scale that one chooses as the renormalization point, and it becomes very interesting to examine the renormalization group running of physical constants under changes in the energy scale. The coupling constants in the Standard Model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
of particle physics vary in different ways with increasing energy scale: the coupling of quantum chromodynamics
Quantum chromodynamics
In theoretical physics, quantum chromodynamics is a theory of the strong interaction , a fundamental force describing the interactions of the quarks and gluons making up hadrons . It is the study of the SU Yang–Mills theory of color-charged fermions...
and the weak isospin coupling of the electroweak force tend to decrease, and the weak hypercharge coupling of the electroweak force tends to increase. At the colossal energy scale of 1015 GeV
GEV
GEV or GeV may stand for:*GeV or gigaelectronvolt, a unit of energy equal to billion electron volts*GEV or Grid Enabled Vehicle that is fully or partially powered by the electric grid, see plug-in electric vehicle...
(far beyond the reach of our current particle accelerator
Particle accelerator
A particle accelerator is a device that uses electromagnetic fields to propel charged particles to high speeds and to contain them in well-defined beams. An ordinary CRT television set is a simple form of accelerator. There are two basic types: electrostatic and oscillating field accelerators.In...
s), they all become approximately the same size (Grotz and Klapdor 1990, p. 254), a major motivation for speculations about grand unified theory. Instead of being only a worrisome problem, renormalization has become an important theoretical tool for studying the behavior of field theories in different regimes.
If a theory featuring renormalization (e.g. QED) can only be sensibly interpreted as an effective field theory, i.e. as an approximation reflecting human ignorance about the workings of nature, then the problem remains of discovering a more accurate theory that does not have these renormalization problems. As Lewis Ryder has put it, "In the Quantum Theory, these [classical] divergences do not disappear; on the contrary, they appear to get worse. And despite the comparative success of renormalisation theory the feeling remains that there ought to be a more satisfactory way of doing things."
Renormalizability
From this philosophical reassessment a new concept follows naturally: the notion of renormalizability. Not all theories lend themselves to renormalization in the manner described above, with a finite supply of counterterms and all quantities becoming cutoff-independent at the end of the calculation. If the Lagrangian contains combinations of field operators of high enough dimensionDimensional analysis
In physics and all science, dimensional analysis is a tool to find or check relations among physical quantities by using their dimensions. The dimension of a physical quantity is the combination of the basic physical dimensions which describe it; for example, speed has the dimension length per...
in energy units, the counterterms required to cancel all divergences proliferate to infinite number, and, at first glance, the theory would seem to gain an infinite number of free parameters and therefore lose all predictive power, becoming scientifically worthless. Such theories are called nonrenormalizable.
The Standard Model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
of particle physics contains only renormalizable operators, but the interactions of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
become nonrenormalizable operators if one attempts to construct a field theory of quantum gravity
Quantum gravity
Quantum gravity is the field of theoretical physics which attempts to develop scientific models that unify quantum mechanics with general relativity...
in the most straightforward manner, suggesting that perturbation theory
Perturbation theory (quantum mechanics)
In quantum mechanics, perturbation theory is a set of approximation schemes directly related to mathematical perturbation for describing a complicated quantum system in terms of a simpler one. The idea is to start with a simple system for which a mathematical solution is known, and add an...
is useless in application to quantum gravity.
However, in an effective field theory
Effective field theory
In physics, an effective field theory is, as any effective theory, an approximate theory, that includes appropriate degrees of freedom to describe physical phenomena occurring at a chosen length scale, while ignoring substructure and degrees of freedom at shorter distances .-The renormalization...
, "renormalizability" is, strictly speaking, a misnomer
Misnomer
A misnomer is a term which suggests an interpretation that is known to be untrue. Such incorrect terms sometimes derive their names because of the form, action, or origin of the subject becoming named popularly or widely referenced—long before their true natures were known.- Sources of misnomers...
. In a nonrenormalizable effective field theory, terms in the Lagrangian do multiply to infinity, but have coefficients suppressed by ever-more-extreme inverse powers of the energy cutoff. If the cutoff is a real, physical quantity—if, that is, the theory is only an effective description of physics up to some maximum energy or minimum distance scale—then these extra terms could represent real physical interactions. Assuming that the dimensionless constants in the theory do not get too large, one can group calculations by inverse powers of the cutoff, and extract approximate predictions to finite order in the cutoff that still have a finite number of free parameters. It can even be useful to renormalize these "nonrenormalizable" interactions.
Nonrenormalizable interactions in effective field theories rapidly become weaker as the energy scale becomes much smaller than the cutoff. The classic example is the Fermi theory
Fermi's interaction
In particle physics, Fermi's interaction also known as Fermi coupling, is an old explanation of the weak force, proposed by Enrico Fermi, in which four fermions directly interact with one another at one vertex...
of the weak nuclear force, a nonrenormalizable effective theory whose cutoff is comparable to the mass of the W particle. This fact may also provide a possible explanation for why almost all of the particle interactions we see are describable by renormalizable theories. It may be that any others that may exist at the GUT or Planck scale simply become too weak to detect in the realm we can observe, with one exception: gravity, whose exceedingly weak interaction is magnified by the presence of the enormous masses of star
Star
A star is a massive, luminous sphere of plasma held together by gravity. At the end of its lifetime, a star can also contain a proportion of degenerate matter. The nearest star to Earth is the Sun, which is the source of most of the energy on Earth...
s and planet
Planet
A planet is a celestial body orbiting a star or stellar remnant that is massive enough to be rounded by its own gravity, is not massive enough to cause thermonuclear fusion, and has cleared its neighbouring region of planetesimals.The term planet is ancient, with ties to history, science,...
s.
Renormalization schemes
In actual calculations, the counterterms introduced to cancel the divergences in Feynman diagram calculations beyond tree level must be fixed using a set of renormalization conditions. The common renormalization schemes in use include:- Minimal subtraction (MS) schemeMinimal subtraction schemeIn quantum field theory, the minimal subtraction scheme, or MS scheme is a particular renormalization scheme used to absorb the infinities that arise in perturbative calculations beyond leading order, introduced independently by and...
and the related modified minimal subtraction (MS-bar) scheme - On-shell schemeOn shell renormalization schemeIn quantum field theory, and especially in quantum electrodynamics, the interacting theory leads to infinite quantities that have to be absorbed in a renormalization procedure, in order to be able to predict measurable quantities. The renormalization scheme can depend on the type of particles that...
Application in statistical physics
As mentioned in the introduction, the methods of renormalization have been applied to Statistical PhysicsStatistical physics
Statistical physics is the branch of physics that uses methods of probability theory and statistics, and particularly the mathematical tools for dealing with large populations and approximations, in solving physical problems. It can describe a wide variety of fields with an inherently stochastic...
, namely to the problems of the critical behaviour near second-order phase transitions, in particular at fictitious spatial dimensions just below the number of 4, where the above-mentioned methods could even be sharpened (i.e., instead of "renormalizability" one gets "super-renormalizability"), which allowed extrapolation to the real spatial dimensionality for phase transitions, 3. Details can be found in the book of Zinn-Justin, mentioned below.
For the discovery of these unexpected applications, and working out the details, in 1982 the physics Nobel prize was awarded to Kenneth G. Wilson
Kenneth G. Wilson
Kenneth Geddes Wilson is an American theoretical physicist and Nobel Prize winner.As an undergraduate at Harvard, he was a Putnam Fellow. He earned his PhD from Caltech in 1961, studying under Murray Gell-Mann....
.
See also
- Effective field theoryEffective field theoryIn physics, an effective field theory is, as any effective theory, an approximate theory, that includes appropriate degrees of freedom to describe physical phenomena occurring at a chosen length scale, while ignoring substructure and degrees of freedom at shorter distances .-The renormalization...
- Landau poleLandau poleIn physics, the Landau pole is the momentum scale at which the coupling constant of a quantum field theory becomes infinite...
- Quantum field theoryQuantum field theoryQuantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
- Quantum trivialityQuantum trivialityIn a quantum field theory, charge screening can restrict the value of the observable "renormalized" charge of a classical theory. Ifthe only allowed value of the renormalized charge is zero, the theory is said to be "trivial" or noninteracting...
- RegularizationRegularization (physics)-Introduction:In physics, especially quantum field theory, regularization is a method of dealing with infinite, divergent, and non-sensical expressions by introducing an auxiliary concept of a regulator...
- Renormalization groupRenormalization groupIn theoretical physics, the renormalization group refers to a mathematical apparatus that allows systematic investigation of the changes of a physical system as viewed at different distance scales...
- Ward–Takahashi identityWard–Takahashi identityIn quantum field theory, a Ward-Takahashi identity is an identity between correlation functions that follows from the global or gauged symmetries of the theory, and which remains valid after renormalization....
- Zeta function regularizationZeta function regularizationIn mathematics and theoretical physics, zeta function regularization is a type of regularization or summability method that assigns finite values to divergent sums or products, and in particular can be used to define determinants and traces of some self-adjoint operators...
- Zeno's paradoxesZeno's paradoxesZeno's paradoxes are a set of problems generally thought to have been devised by Greek philosopher Zeno of Elea to support Parmenides's doctrine that "all is one" and that, contrary to the evidence of our senses, the belief in plurality and change is mistaken, and in particular that motion is...
General introduction
- Delamotte, Bertrand ; , American Journal of Physics 72 (2004) pp. 170–184. Beautiful elementary introduction to the ideas, no prior knowledge of field theory being necessary. Full text available at: hep-th/0212049
- Baez, John ; Renormalization Made Easy, (2005). A qualitative introduction to the subject.
- Blechman, Andrew E. ; Renormalization: Our Greatly Misunderstood Friend, (2002). Summary of a lecture; has more information about specific regularization and divergence-subtraction schemes.
- Cao, Tian Yu & Schweber, Silvian S. ; , Synthese, 97(1) (1993), 33–108.
- Shirkov, DmitryDmitry ShirkovDmitry Vasil'evich Shirkov is a Russian theoretical physicist known for his contribution to quantum field theory and to the development of the renormalization group method.-Biography:...
; Fifty Years of the Renormalization Group, C.E.R.N. Courrier 41(7) (2001). Full text available at : I.O.P Magazines. - E. Elizalde ; Zeta regularization techniques with Applications.
Mainly: quantum field theory
- N. N. Bogoliubov, D. V. ShirkovDmitry ShirkovDmitry Vasil'evich Shirkov is a Russian theoretical physicist known for his contribution to quantum field theory and to the development of the renormalization group method.-Biography:...
(1959): The Theory of Quantized Fields. New York, Interscience. The first text-book on the renormalization groupRenormalization groupIn theoretical physics, the renormalization group refers to a mathematical apparatus that allows systematic investigation of the changes of a physical system as viewed at different distance scales...
theory. - Ryder, Lewis H. ; Quantum Field Theory (Cambridge University Press, 1985), ISBN 0-521-33859-X Highly readable textbook, certainly the best introduction to relativistic Q.F.T. for particle physics.
- Zee, Anthony ; Quantum Field Theory in a Nutshell, Princeton University Press (2003) ISBN 0-691-01019-6. Another excellent textbook on Q.F.T.
- Weinberg, Steven ; The Quantum Theory of Fields (3 volumes) Cambridge University Press (1995). A monumental treatise on Q.F.T. written by a leading expert, Nobel laureate 1979.
- Pokorski, Stefan ; Gauge Field Theories, Cambridge University Press (1987) ISBN 0-521-47816-2.
- 't Hooft, Gerard ; The Glorious Days of Physics – Renormalization of Gauge theories, lecture given at Erice (August/September 1998) by the Nobel laureate 1999 . Full text available at: hep-th/9812203.
- Rivasseau, Vincent ; An introduction to renormalization, Poincaré Seminar (Paris, Oct. 12, 2002), published in : Duplantier, Bertrand; Rivasseau, Vincent (Eds.) ; Poincaré Seminar 2002, Progress in Mathematical Physics 30, Birkhäuser (2003) ISBN 3-7643-0579-7. Full text available in PostScript.
- Rivasseau, Vincent ; From perturbative to constructive renormalization, Princeton University Press (1991) ISBN 0-691-08530-7. Full text available in PostScript.
- Iagolnitzer, Daniel & Magnen, J. ; Renormalization group analysis, Encyclopaedia of Mathematics, Kluwer Academic Publisher (1996). Full text available in PostScript and pdf here.
- Scharf, Günter; Finite quantum electrodynamics: The causal approach, Springer Verlag Berlin Heidelberg New York (1995) ISBN 3-540-60142-2.
- A. S. Švarc (Albert SchwarzAlbert SchwarzAlbert S. Schwarz is a mathematician and a theoretical physicist educated in Soviet Union and now a Professor at the University of California-Davis. He is one of the pioneers of Morse theory and brought up the first example of a topological quantum field theory. Schwarz worked on some examples in...
), Математические основы квантовой теории поля, (Mathematical aspects of quantum field theory), Atomizdat, Moscow, 1975. 368 pp.
Mainly: statistical physics
- A. N. Vasil'ev The Field Theoretic Renormalization Group in Critical Behavior Theory and Stochastic Dynamics (Routledge Chapman & Hall 2004); ISBN 978-0415310024
- Nigel Goldenfeld ; Lectures on Phase Transitions and the Renormalization Group, Frontiers in Physics 85, Westview Press (June, 1992) ISBN 0-201-55409-7. Covering the elementary aspects of the physics of phases transitions and the renormalization group, this popular book emphasizes understanding and clarity rather than technical manipulations.
- Zinn-Justin, Jean ; Quantum Field Theory and Critical Phenomena, Oxford University Press (4th edition – 2002) ISBN 0-19-850923-5. A masterpiece on applications of renormalization methods to the calculation of critical exponents in statistical mechanics, following Wilson's ideas (Kenneth Wilson was Nobel laureate 1982).
- Zinn-Justin, Jean ; Phase Transitions & Renormalization Group: from Theory to Numbers, Poincaré Seminar (Paris, Oct. 12, 2002), published in : Duplantier, Bertrand; Rivasseau, Vincent (Eds.) ; Poincaré Seminar 2002, Progress in Mathematical Physics 30, Birkhäuser (2003) ISBN 3-7643-0579-7. Full text available in PostScript.
- Domb, Cyril ; The Critical Point: A Historical Introduction to the Modern Theory of Critical Phenomena, CRC Press (March, 1996) ISBN 0-7484-0435-X.
- Brown, Laurie M. (Ed.) ; Renormalization: From Lorentz to Landau (and Beyond), Springer-Verlag (New York-1993) ISBN 0-387-97933-6.
- Cardy, JohnJohn CardyJohn Lawrence Cardy FRS is a British theoretical physicist at the University of Oxford. He is best known for his work in theoretical condensed matter physics and statistical mechanics, and in particular for research on critical phenomena and conformal field theory.He was an undergraduate and...
; Scaling and Renormalization in Statistical Physics, Cambridge University Press (1996) ISBN 0-521-49959-3.
Miscellaneous
- Shirkov, DmitryDmitry ShirkovDmitry Vasil'evich Shirkov is a Russian theoretical physicist known for his contribution to quantum field theory and to the development of the renormalization group method.-Biography:...
; The Bogoliubov Renormalization Group, JINR Communication E2-96-15 (1996). Full text available at: hep-th/9602024 - Zinn Justin, Jean ; Renormalization and renormalization group: From the discovery of UV divergences to the concept of effective field theories, in: de Witt-Morette C., Zuber J.-B. (eds), Proceedings of the NATO ASI on Quantum Field Theory: Perspective and Prospective, June 15–26, 1998, Les Houches, France, Kluwer Academic Publishers, NATO ASI Series C 530, 375–388 (1999). Full text available in PostScript.
- Connes, Alain ; Symétries Galoisiennes & Renormalisation, Poincaré Seminar (Paris, Oct. 12, 2002), published in : Duplantier, Bertrand; Rivasseau, Vincent (Eds.) ; Poincaré Seminar 2002, Progress in Mathematical Physics 30, Birkhäuser (2003) ISBN 3-7643-0579-7. French mathematician Alain Connes (Fields medallist 1982) describe the mathematical underlying structure (the Hopf algebraHopf algebraIn mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property.Hopf algebras occur naturally...
) of renormalization, and its link to the Riemann-Hilbert problem. Full text (in French) available at math/0211199v1.