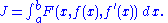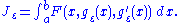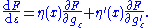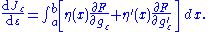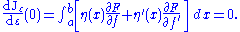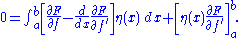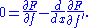Euler-Lagrange equation
Encyclopedia
In calculus of variations
, the Euler–Lagrange equation, Euler's equation, or Lagrange's equation, is a differential equation
whose solutions are the function
s for which a given functional
is stationary
. It was developed by Swiss mathematician Leonhard Euler
and Italian mathematician Joseph Louis Lagrange
in the 1750s.
Because a differentiable functional is stationary at its local maxima and minima
, the Euler–Lagrange equation is useful for solving optimization
problems in which, given some functional, one seeks the function minimizing (or maximizing) it. This is analogous to Fermat's theorem
in calculus
, stating that where a differentiable function attains its local extrema, its derivative is zero.
In Lagrangian mechanics
, because of Hamilton's principle
of stationary action, the evolution of a physical system is described by the solutions to the Euler–Lagrange equation for the action of the system. In classical mechanics
, it is equivalent to Newton's laws of motion
, but it has the advantage that it takes the same form in any system of generalized coordinates, and it is better suited to generalizations (see, for example, the "Field theory" section below).
Lagrange solved this problem in 1755 and sent the solution to Euler. The two further developed Lagrange's method and applied it to mechanics
, which led to the formulation of Lagrangian mechanics
. Their correspondence ultimately led to the calculus of variations, a term coined by Euler himself in 1766.
of a real
argument, t, which is a stationary point of the functional

where:
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
, the Euler–Lagrange equation, Euler's equation, or Lagrange's equation, is a differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
whose solutions are the function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s for which a given functional
Functional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
is stationary
Stationary point
In mathematics, particularly in calculus, a stationary point is an input to a function where the derivative is zero : where the function "stops" increasing or decreasing ....
. It was developed by Swiss mathematician Leonhard Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
and Italian mathematician Joseph Louis Lagrange
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
in the 1750s.
Because a differentiable functional is stationary at its local maxima and minima
Maxima and minima
In mathematics, the maximum and minimum of a function, known collectively as extrema , are the largest and smallest value that the function takes at a point either within a given neighborhood or on the function domain in its entirety .More generally, the...
, the Euler–Lagrange equation is useful for solving optimization
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
problems in which, given some functional, one seeks the function minimizing (or maximizing) it. This is analogous to Fermat's theorem
Fermat's theorem (stationary points)
In mathematics, Fermat's theorem is a method to find local maxima and minima of differentiable functions on open sets by showing that every local extremum of the function is a stationary point...
in calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
, stating that where a differentiable function attains its local extrema, its derivative is zero.
In Lagrangian mechanics
Lagrangian mechanics
Lagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
, because of Hamilton's principle
Hamilton's principle
In physics, Hamilton's principle is William Rowan Hamilton's formulation of the principle of stationary action...
of stationary action, the evolution of a physical system is described by the solutions to the Euler–Lagrange equation for the action of the system. In classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
, it is equivalent to Newton's laws of motion
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
, but it has the advantage that it takes the same form in any system of generalized coordinates, and it is better suited to generalizations (see, for example, the "Field theory" section below).
History
The Euler–Lagrange equation was developed in the 1750s by Euler and Lagrange in connection with their studies of the tautochrone problem. This is the problem of determining a curve on which a weighted particle will fall to a fixed point in a fixed amount of time, independent of the starting point.Lagrange solved this problem in 1755 and sent the solution to Euler. The two further developed Lagrange's method and applied it to mechanics
Mechanics
Mechanics is the branch of physics concerned with the behavior of physical bodies when subjected to forces or displacements, and the subsequent effects of the bodies on their environment....
, which led to the formulation of Lagrangian mechanics
Lagrangian mechanics
Lagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
. Their correspondence ultimately led to the calculus of variations, a term coined by Euler himself in 1766.
Statement
The Euler–Lagrange equation is an equation satisfied by a function, q,of a real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
argument, t, which is a stationary point of the functional
Functional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...

where:
- q is the function to be found:
- such that q is differentiable, q(a) = xa, and q(b) = xb;
- q′ is the derivative of q:
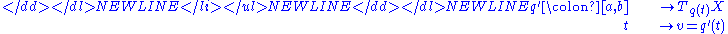
- TX being the tangent bundleTangent bundleIn differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
of X (the space of possible values of derivatives of functions with values in X);- L is a real-valued function with continuousContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
first partial derivatives:
The Euler–Lagrange equation, then, is given by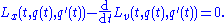
where Lx and Lv denote the partial derivatives of L with respect to the second and third arguments, respectively.
If the dimension of the space X is greater than 1, this is a system of differential equations, one for each component:
Derivation of one-dimensional Euler–Lagrange equation
The derivation of the one-dimensional Euler–Lagrange equation is one of the classic proofs in mathematicsMathematicsMathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
. It relies on the fundamental lemma of calculus of variationsFundamental lemma of calculus of variationsIn mathematics, specifically in the calculus of variations, the fundamental lemma in the calculus of variations is a lemma that is typically used to transform a problem from its weak formulation into its strong formulation .-Statement:A function is said to be of class C^k if it is k-times...
.
We wish to find a function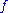 which satisfies the boundary conditions
which satisfies the boundary conditions 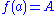 ,
, 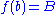 , and which extremizes the cost functional
, and which extremizes the cost functional
We assume that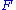 has continuous first partial derivatives. A weaker assumption can be used, but the proof becomes more difficult.
has continuous first partial derivatives. A weaker assumption can be used, but the proof becomes more difficult.
If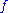 extremizes the cost functional subject to the boundary conditions, then any slight perturbation of
extremizes the cost functional subject to the boundary conditions, then any slight perturbation of  that preserves the boundary values must either increase
that preserves the boundary values must either increase 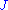 (if
(if 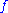 is a minimizer) or decrease
is a minimizer) or decrease 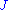 (if
(if 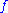 is a maximizer).
is a maximizer).
Let be such a perturbation of
be such a perturbation of 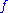 , where
, where  is a differentiable function satisfying
is a differentiable function satisfying 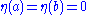 . Then define
. Then define
We now wish to calculate the total derivativeTotal derivativeIn the mathematical field of differential calculus, the term total derivative has a number of closely related meanings.The total derivative of a function f, of several variables, e.g., t, x, y, etc., with respect to one of its input variables, e.g., t, is different from the partial derivative...
of J with respect to ε or the first variationFirst variationIn applied mathematics and the calculus of variations, the first variation of a functional J is defined as the linear functional \delta J mapping the function h to...
of J.
It follows from the total derivative that
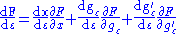
So
When ε = 0 we have gε = f and since f is an extreme value it follows that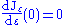 , i.e.
, i.e.
The next crucial step is to use integration by partsIntegration by partsIn calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...
on the second term, yielding
Using the boundary conditions on η, we get that
Applying the fundamental lemma of calculus of variationsFundamental lemma of calculus of variationsIn mathematics, specifically in the calculus of variations, the fundamental lemma in the calculus of variations is a lemma that is typically used to transform a problem from its weak formulation into its strong formulation .-Statement:A function is said to be of class C^k if it is k-times...
now yields the Euler–Lagrange equation
-
Alternate derivation of one-dimensional Euler–Lagrange equation
Given a functional
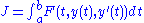
on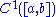 with the boundary conditions
with the boundary conditions 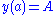 and
and 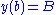 , we proceed by approximating the extremal curve by a polygonal line with
, we proceed by approximating the extremal curve by a polygonal line with  segments and passing to the limit as the number of segments grows arbitrarily large.
segments and passing to the limit as the number of segments grows arbitrarily large.
Divide the interval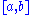 into
into  equal segments with endpoints
equal segments with endpoints  and let
and let 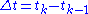 . Rather than a smooth function
. Rather than a smooth function  we consider the polygonal line with vertices
we consider the polygonal line with vertices 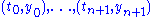 , where
, where 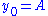 and
and 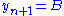 . Accordingly, our functional becomes a real function of
. Accordingly, our functional becomes a real function of  variables given by
variables given by
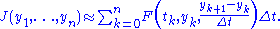
Extremals of this new functional defined on the discrete points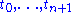 correspond to points where
correspond to points where

Evaluating this partial derivative gives
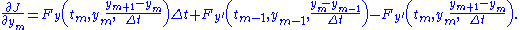
Dividing the above equation by gives
gives
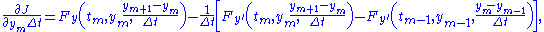
and taking the limit as of the right-hand side of this expression yields
of the right-hand side of this expression yields
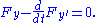
The left hand side of the previous equation is the functional derivativeFunctional derivativeIn mathematics and theoretical physics, the functional derivative is a generalization of the gradient. While the latter differentiates with respect to a vector with discrete components, the former differentiates with respect to a continuous function. Both of these can be viewed as extensions of...
 of the functional
of the functional 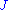 . A necessary condition for a differentiable functional to have an extremum on some function is that its functional derivative at that function vanishes, which is granted by the last equation.
. A necessary condition for a differentiable functional to have an extremum on some function is that its functional derivative at that function vanishes, which is granted by the last equation.
Examples
A standard example is finding the real-valued function on the interval [a, b], such that f(a) = c and f(b) = d, the lengthArc lengthDetermining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves...
of whose graphGraph of a functionIn mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
is as short as possible. The length of the graph of f is: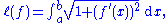
the integrand function being evaluated at .
The partial derivatives of L are:
By substituting these into the Euler–Lagrange equation, we obtain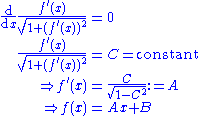
that is, the function must have constant first derivative, and thus its graph is a straight line.
Basic method
To find the equations of motions for a given system, one only has to follow these steps:- From the kinetic energy
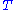 , and the potential energy
, and the potential energy 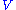 , compute the Lagrangian
, compute the Lagrangian  .
. - Compute
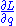 .
. - Compute
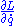 and from it,
and from it, 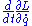 . It is important that
. It is important that 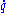 be treated as a complete variable in its own right, and not as a derivative.
be treated as a complete variable in its own right, and not as a derivative. - Equate
 . This is the Euler–Lagrange equation.
. This is the Euler–Lagrange equation. - Solve the differential equation obtained in the preceding step. At this point,
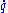 is treated "normally". Note that the above might be a system of equations and not simply one equation.
is treated "normally". Note that the above might be a system of equations and not simply one equation.
Particle in a conservative force field
The motion of a single particle in a conservative forceConservative forceA conservative force is a force with the property that the work done in moving a particle between two points is independent of the path taken. Equivalently, if a particle travels in a closed loop, the net work done by a conservative force is zero.It is possible to define a numerical value of...
field (for example, the gravitational force) can be determined by requiring the action to be stationary, by Hamilton's principleHamilton's principleIn physics, Hamilton's principle is William Rowan Hamilton's formulation of the principle of stationary action...
. The action for this system is
where x(t) is the position of the particle at time t. The dot above is Newton's notation for the time derivative: thus ẋ(t) is the particle velocity, v(t). In the equation above, L is the LagrangianLagrangianThe Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
(the kinetic energyKinetic energyThe kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
minus the potential energyPotential energyIn physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
):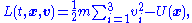
where:- m is the mass of the particle (assumed to be constantConservation of massThe law of conservation of mass, also known as the principle of mass/matter conservation, states that the mass of an isolated system will remain constant over time...
in classical physics); - vi is the i-th component of the vector v in a Cartesian coordinate system (the same notation will be used for other vectors);
- U is the potential of the conservative force.
In this case, the Lagrangian does not vary with its first argument t. (By Noether's theoremNoether's theoremNoether's theorem states that any differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proved by German mathematician Emmy Noether in 1915 and published in 1918...
, such symmetries of the system correspond to conservation lawConservation lawIn physics, a conservation law states that a particular measurable property of an isolated physical system does not change as the system evolves....
s. In particular, the invariance of the Lagrangian with respect to time implies the conservation of energyConservation of energyThe nineteenth century law of conservation of energy is a law of physics. It states that the total amount of energy in an isolated system remains constant over time. The total energy is said to be conserved over time...
.)
By partial differentiation of the above Lagrangian, we find: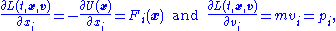
where the force is F = −∇U (the negative gradientGradientIn vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of the potential, by definition of conservative force), and p is the momentumMomentumIn classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
.
By substituting these into the Euler–Lagrange equation, we obtain a system of second-order differential equations for the coordinates on the particle's trajectory,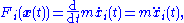
which can be solved on the interval [t0, t1], given the boundary values xi(t0) and xi(t1).
In vector notation, this system reads
or, using the momentum,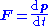
which is Newton's second law.
Single function of single variable with higher derivatives
The stationary values of the functional
can be obtained from the Euler–Lagrange equation
Several functions of one variable
If the problem involves finding several functions (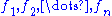 ) of a single independent variable (
) of a single independent variable ( ) that define an extremum of the functional
) that define an extremum of the functional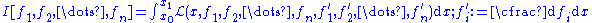
then the corresponding Euler–Lagrange equations are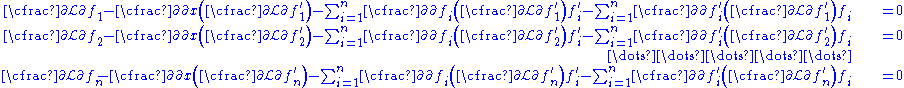
Single function of several variables
A multi-dimensional generalization comes from considering a function on n variables. If Ω is some surface, then
-

is extremized only if f satisfies the partial differential equationPartial differential equationIn mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
When n = 2 and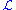 is the energy functionalEnergy functionalEnergy functional is total energy of a certain system, as a function of the system's state.In the energy methods of simulating the dynamics of complex structures, a state of the system is often described as an element of an appropriate function space. To be in this state, the system pays a certain...
is the energy functionalEnergy functionalEnergy functional is total energy of a certain system, as a function of the system's state.In the energy methods of simulating the dynamics of complex structures, a state of the system is often described as an element of an appropriate function space. To be in this state, the system pays a certain...
, this leads to the soap-film minimal surfaceMinimal surfaceIn mathematics, a minimal surface is a surface with a mean curvature of zero.These include, but are not limited to, surfaces of minimum area subject to various constraints....
problem.
Several functions of several variables
If there are several unknown functions to be determined and several variables such that-

the system of Euler–Lagrange equations is-

Single function of two variables with higher derivatives
If there is a single unknown function to be determined that is dependent on two variables and their higher derivatives such that-
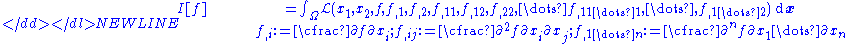
the Euler–Lagrange equation is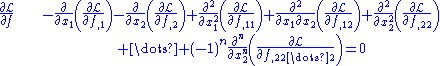
See also
- Lagrangian mechanicsLagrangian mechanicsLagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
- Hamiltonian mechanicsHamiltonian mechanicsHamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
- Analytical mechanicsAnalytical mechanicsAnalytical mechanics is a term used for a refined, mathematical form of classical mechanics, constructed from the 18th century onwards as a formulation of the subject as founded by Isaac Newton. Often the term vectorial mechanics is applied to the form based on Newton's work, to contrast it with...
- Beltrami identityBeltrami identityThe Beltrami identity is an identity in the calculus of variations. It says that a function u which is an extremal of the integralI=\int_a^b L \, dxsatisfies the differential equation...
- Lagrangian mechanics
-
-
-
- L is a real-valued function with continuous
- TX being the tangent bundle
- q′ is the derivative of q:
- such that q is differentiable, q(a) = xa, and q(b) = xb;