Self-energy
Encyclopedia
In theoretical physics
and quantum field theory
a particle's self-energy
represents the contribution to the particle's energy
, or effective mass
, due to interactions between the particle and the system it is part of. For example, in electrostatics
the self-energy of a given charge distribution is the energy required to assemble the distribution by bringing in the constituent charges from infinity, where the electric force goes to zero. In a condensed matter
context relevant to electrons moving in a material, the self-energy represents the potential felt by the electron due to the surrounding medium's interactions with it: for example, the fact that electrons repel each other means that a moving electron polarizes (causes to displace) the electrons in its vicinity and this in turn changes the potential the moving electron feels; these and other effects are included in the self-energy.
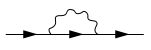
Mathematically, this energy is equal to the so-called on-the-mass-shell value of the proper self-energy operator (or proper mass operator) in the momentum-energy representation (more precisely, to
times this value). In this, or other representations (such as the space-time representation), the self-energy is pictorially (and economically) represented by means of Feynman diagrams, such as the one shown below. In this particular diagram, the three arrowed straight lines represent particles, or particle propagators, and the wavy line a particle-particle interaction; removing (or amputating) the left-most and the right-most straight lines in the diagram shown below (these so-called external lines correspond to prescribed values for, for instance, momentum and energy, or four-momentum), one retains a contribution to the self-energy operator (in, for instance, the momentum-energy representation). Using a small number of simple rules, each Feynman diagram
can be readily expressed in its corresponding algebraic form.
In general, the on-the-mass-shell value of the self-energy operator in the momentum-energy representation is complex (see complex number
). In such cases, it is the real part of this self-energy that is identified with the physical self-energy (referred to above as particle's self-energy); the inverse of the imaginary part is a measure for the lifetime of the particle under investigation. For clarity, elementary excitations, or dressed particles (see quasi-particle), in interacting systems are distinct from stable particles in vacuum; their state functions consist of complicated superpositions of the eigenstates of the underlying many-particle system, which only, if at all, momentarily behave like those specific to isolated particles; the above-mentioned lifetime is the time over which a dressed particle behaves as if it were a single particle with well-defined momentum and energy.
The self-energy operator (often denoted by
, and less frequently by 
) is related to the bare and dressed propagator
s (often denoted by
and 
respectively) via the Dyson equation (named after Freeman John Dyson):
.
Multiplying on the left by the inverse
of the operator 
and on the right by
yields
.
The photon
and gluon
do not get a mass through renormalization because gauge symmetry protects them from getting a mass. This is a consequence of the Ward identity. The W-boson and the Z-boson get their masses through the Higgs mechanism
; they do undergo mass renormalization through the renormalization of the electroweak theory.
Neutral particles with internal quantum numbers can mix with each other through virtual pair production. The primary example of this phenomenon is the mixing of neutral kaon
s. Under appropriate simplifying assumptions this can be described without quantum field theory
.
In chemistry
, the self-energy or Born energy of an ion is the energy associated with the field of the ion itself.
In solid state
and condensed-matter physics self-energies and a myriad of related Quasiparticle
properties are calculated by Green's function
methods and Green's function (many-body theory)
of interacting low-energy excitations on the basis of electronic band structure
calculations.
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
and quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
a particle's self-energy
represents the contribution to the particle's energyEnergy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
, or effective mass
Effective mass
In solid state physics, a particle's effective mass is the mass it seems to carry in the semiclassical model of transport in a crystal. It can be shown that electrons and holes in a crystal respond to electric and magnetic fields almost as if they were particles with a mass dependence in their...
, due to interactions between the particle and the system it is part of. For example, in electrostatics
Electrostatics
Electrostatics is the branch of physics that deals with the phenomena and properties of stationary or slow-moving electric charges....
the self-energy of a given charge distribution is the energy required to assemble the distribution by bringing in the constituent charges from infinity, where the electric force goes to zero. In a condensed matter
Condensed Matter
Condensed matter may refer to several things*Condensed matter physics, the study of the physical properties of condensed phases of matter*European Physical Journal B: Condensed Matter and Complex Systems, a scientific journal published by EDP sciences...
context relevant to electrons moving in a material, the self-energy represents the potential felt by the electron due to the surrounding medium's interactions with it: for example, the fact that electrons repel each other means that a moving electron polarizes (causes to displace) the electrons in its vicinity and this in turn changes the potential the moving electron feels; these and other effects are included in the self-energy.
Mathematically, this energy is equal to the so-called on-the-mass-shell value of the proper self-energy operator (or proper mass operator) in the momentum-energy representation (more precisely, to
times this value). In this, or other representations (such as the space-time representation), the self-energy is pictorially (and economically) represented by means of Feynman diagrams, such as the one shown below. In this particular diagram, the three arrowed straight lines represent particles, or particle propagators, and the wavy line a particle-particle interaction; removing (or amputating) the left-most and the right-most straight lines in the diagram shown below (these so-called external lines correspond to prescribed values for, for instance, momentum and energy, or four-momentum), one retains a contribution to the self-energy operator (in, for instance, the momentum-energy representation). Using a small number of simple rules, each Feynman diagramFeynman diagram
Feynman diagrams are a pictorial representation scheme for the mathematical expressions governing the behavior of subatomic particles, first developed by the Nobel Prize-winning American physicist Richard Feynman, and first introduced in 1948...
can be readily expressed in its corresponding algebraic form.
In general, the on-the-mass-shell value of the self-energy operator in the momentum-energy representation is complex (see complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
). In such cases, it is the real part of this self-energy that is identified with the physical self-energy (referred to above as particle's self-energy); the inverse of the imaginary part is a measure for the lifetime of the particle under investigation. For clarity, elementary excitations, or dressed particles (see quasi-particle), in interacting systems are distinct from stable particles in vacuum; their state functions consist of complicated superpositions of the eigenstates of the underlying many-particle system, which only, if at all, momentarily behave like those specific to isolated particles; the above-mentioned lifetime is the time over which a dressed particle behaves as if it were a single particle with well-defined momentum and energy.
The self-energy operator (often denoted by
, and less frequently by ) is related to the bare and dressed propagatorPropagator
In quantum mechanics and quantum field theory, the propagator gives the probability amplitude for a particle to travel from one place to another in a given time, or to travel with a certain energy and momentum. Propagators are used to represent the contribution of virtual particles on the internal...
s (often denoted by
and respectively) via the Dyson equation (named after Freeman John Dyson):.Multiplying on the left by the inverse
of the operator and on the right by
yields.
The photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
and gluon
Gluon
Gluons are elementary particles which act as the exchange particles for the color force between quarks, analogous to the exchange of photons in the electromagnetic force between two charged particles....
do not get a mass through renormalization because gauge symmetry protects them from getting a mass. This is a consequence of the Ward identity. The W-boson and the Z-boson get their masses through the Higgs mechanism
Higgs mechanism
In particle physics, the Higgs mechanism is the process in which gauge bosons in a gauge theory can acquire non-vanishing masses through absorption of Nambu-Goldstone bosons arising in spontaneous symmetry breaking....
; they do undergo mass renormalization through the renormalization of the electroweak theory.
Neutral particles with internal quantum numbers can mix with each other through virtual pair production. The primary example of this phenomenon is the mixing of neutral kaon
Kaon
In particle physics, a kaon is any one of a group of four mesons distinguished by the fact that they carry a quantum number called strangeness...
s. Under appropriate simplifying assumptions this can be described without quantum field theory
Neutral particle oscillations
In particle physics, neutral particle oscillation is the transmutation of a neutral particle with nonzero internal quantum numbers into its antiparticle...
.
In chemistry
Chemistry
Chemistry is the science of matter, especially its chemical reactions, but also its composition, structure and properties. Chemistry is concerned with atoms and their interactions with other atoms, and particularly with the properties of chemical bonds....
, the self-energy or Born energy of an ion is the energy associated with the field of the ion itself.
In solid state
Solid-state physics
Solid-state physics is the study of rigid matter, or solids, through methods such as quantum mechanics, crystallography, electromagnetism, and metallurgy. It is the largest branch of condensed matter physics. Solid-state physics studies how the large-scale properties of solid materials result from...
and condensed-matter physics self-energies and a myriad of related Quasiparticle
Quasiparticle
In physics, quasiparticles are emergent phenomena that occur when a microscopically complicated system such as a solid behaves as if it contained different weakly interacting particles in free space...
properties are calculated by Green's function
Green's function
In mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
methods and Green's function (many-body theory)
Green's function (many-body theory)
In many-body theory, the term Green's function is sometimes used interchangeably with correlation function, but refers specifically to correlators of field operators or creation and annihilation operators....
of interacting low-energy excitations on the basis of electronic band structure
Electronic band structure
In solid-state physics, the electronic band structure of a solid describes those ranges of energy an electron is "forbidden" or "allowed" to have. Band structure derives from the diffraction of the quantum mechanical electron waves in a periodic crystal lattice with a specific crystal system and...
calculations.
See also
- Quantum field theoryQuantum field theoryQuantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
- RenormalizationRenormalizationIn quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities....
- GW approximationGW approximationThe GW approximation is an approximation made in order to calculate the self-energy of a many-body system of electrons. The approximation is that the expansion of the self-energy Σ in terms of the single particle Green function G and the screened Coulomb interaction W can be truncated after the...
- Wheeler-Feynman absorber theory