
Dyson series
Encyclopedia
In scattering theory
, the Dyson series, formulated by British-born American physicist Freeman Dyson
, is a perturbative series, and each term is represented by Feynman diagram
s. This series diverges asymptotically, but in quantum electrodynamics
(QED) at the second order the difference from experimental data is in the order of 10−10. This close agreement holds because the coupling constant (also known as the fine structure constant) of QED
is much less than 1. Notice that in this article Planck units
are used, so that ħ (the reduced Planck constant
) satisfies ħ = 1.
H which we split into a "free" part H0 and an "interacting" part V i.e. H = H0 + V. We will work in the interaction picture
here and assume units such that the reduced Planck constant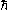 is 1.
is 1.
In the interaction picture, the evolution operator U defined by the equation:

is called Dyson operator.
We have
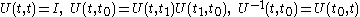
and then (Tomonaga-Schwinger equation
)
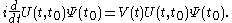
Thus:

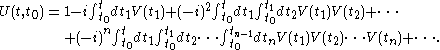
Here we have t1 > t2 > ..., > tn so we can say that the fields are time ordered, and it is useful to introduce an operator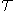 called time-ordering operator, defining:
called time-ordering operator, defining:
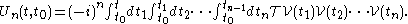
We can now try to make this integration simpler. in fact, by the following example:
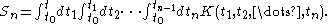
Assume that K is symmetric in its arguments and define (look at integration limits):
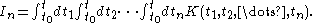
The region of integration can be broken in n! sub-regions defined by
t1 > t2 > ... > tn,
t2 > t1 > ... > tn,
etc. Due to the symmetry of K, the integral in each of these sub-regions is the same, and equal to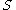 n by definition. So it is true that:
n by definition. So it is true that:
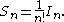
Returning to our previous integral, it holds the identity:
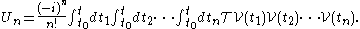
Summing up all the terms we obtain the Dyson series:
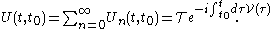

Returning to the Schrödinger picture
, for tf > ti,

Scattering theory
In mathematics and physics, scattering theory is a framework for studying and understanding the scattering of waves and particles. Prosaically, wave scattering corresponds to the collision and scattering of a wave with some material object, for instance sunlight scattered by rain drops to form a...
, the Dyson series, formulated by British-born American physicist Freeman Dyson
Freeman Dyson
Freeman John Dyson FRS is a British-born American theoretical physicist and mathematician, famous for his work in quantum field theory, solid-state physics, astronomy and nuclear engineering. Dyson is a member of the Board of Sponsors of the Bulletin of the Atomic Scientists...
, is a perturbative series, and each term is represented by Feynman diagram
Feynman diagram
Feynman diagrams are a pictorial representation scheme for the mathematical expressions governing the behavior of subatomic particles, first developed by the Nobel Prize-winning American physicist Richard Feynman, and first introduced in 1948...
s. This series diverges asymptotically, but in quantum electrodynamics
Quantum electrodynamics
Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
(QED) at the second order the difference from experimental data is in the order of 10−10. This close agreement holds because the coupling constant (also known as the fine structure constant) of QED
Quantum electrodynamics
Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
is much less than 1. Notice that in this article Planck units
Planck units
In physics, Planck units are physical units of measurement defined exclusively in terms of five universal physical constants listed below, in such a manner that these five physical constants take on the numerical value of 1 when expressed in terms of these units. Planck units elegantly simplify...
are used, so that ħ (the reduced Planck constant
Planck constant
The Planck constant , also called Planck's constant, is a physical constant reflecting the sizes of energy quanta in quantum mechanics. It is named after Max Planck, one of the founders of quantum theory, who discovered it in 1899...
) satisfies ħ = 1.
The Dyson operator
We suppose we have a HamiltonianHamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
H which we split into a "free" part H0 and an "interacting" part V i.e. H = H0 + V. We will work in the interaction picture
Interaction picture
In quantum mechanics, the Interaction picture is an intermediate between the Schrödinger picture and the Heisenberg picture. Whereas in the other two pictures either the state vector or the operators carry time dependence, in the interaction picture both carry part of the time dependence of...
here and assume units such that the reduced Planck constant
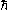 is 1.
is 1.In the interaction picture, the evolution operator U defined by the equation:

is called Dyson operator.
We have
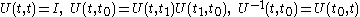
and then (Tomonaga-Schwinger equation
Interaction picture
In quantum mechanics, the Interaction picture is an intermediate between the Schrödinger picture and the Heisenberg picture. Whereas in the other two pictures either the state vector or the operators carry time dependence, in the interaction picture both carry part of the time dependence of...
)
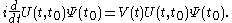
Thus:

Derivation of the Dyson series
This leads to the following Neumann series: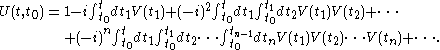
Here we have t1 > t2 > ..., > tn so we can say that the fields are time ordered, and it is useful to introduce an operator
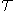 called time-ordering operator, defining:
called time-ordering operator, defining: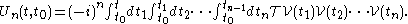
We can now try to make this integration simpler. in fact, by the following example:
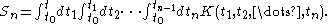
Assume that K is symmetric in its arguments and define (look at integration limits):
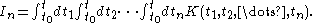
The region of integration can be broken in n! sub-regions defined by
t1 > t2 > ... > tn,
t2 > t1 > ... > tn,
etc. Due to the symmetry of K, the integral in each of these sub-regions is the same, and equal to
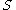 n by definition. So it is true that:
n by definition. So it is true that: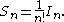
Returning to our previous integral, it holds the identity:
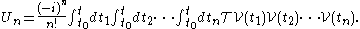
Summing up all the terms we obtain the Dyson series:
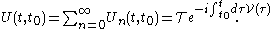
The Dyson series for wavefunctions
Then, going back to the wavefunction for t > t0,
Returning to the Schrödinger picture
Schrödinger picture
In physics, the Schrödinger picture is a formulation of quantum mechanics in which the state vectors evolve in time, but the operators are constant. This differs from the Heisenberg picture which keeps the states constant while the observables evolve in time...
, for tf > ti,


