Ward–Takahashi identity
Encyclopedia
In quantum field theory
, a Ward-Takahashi identity is an identity between correlation functions
that follows from the global or gauged symmetries
of the theory, and which remains valid after renormalization
.
The Ward-Takahashi identity of quantum electrodynamics
was originally used by John Clive Ward
and Yasushi Takahashi
to relate the wave function renormalization
of the electron
to its vertex renormalization factor
F1(0), guaranteeing the cancellation of the ultraviolet divergence
to all orders in perturbation theory. Later uses include the extension of the proof of Goldstone's theorem to all orders of perturbation theory.
The Ward-Takahashi identity is a quantum version of the classical Noether's theorem
, and any symmetries in a quantum field theory can lead to an equation of motion for correlation functions. This generalized sense should be distinguished when reading literature, such as Michael Peskin
and Daniel Schroeder's textbook, An Introduction to Quantum Field Theory (see references), from the original sense of the Ward identity.
be a QED
correlation function
involving an external photon
with momentum k (where
is the polarization
vector of the photon), n initial-state electron
s with momenta
, and n final-state electrons with momenta 
. Also define 
to be the simpler amplitude
that is obtained by removing the photon with momentum k from our original amplitude. Then the Ward-Takahashi identity reads
where −e is the charge of the electron
. Note that if
has its external electrons on-shell, then the amplitudes on the right-hand side of this identity each have one external particle off-shell, and therefore they do not contribute to S-matrix elements.
processes and thus have all their external particles on-shell. Again let
be the amplitude for some QED process involving an external photon with momentum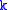 
, where 
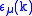is the polarization
vector of the photon. Then the Ward identity reads:
Physically, what this identity means is the longitudinal polarization of the photon which arises in the ξ gauge is unphysical and disappears from the S-matrix.
Examples of its use include constraining the tensor
structure of the vacuum polarization
and of the electron vertex function
in QED.
In the path integral formulation, the Ward-Takahashi identities are a reflection of the invariance of the functional measure under a gauge transformation. More precisely, if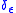
represents a gauge transformation by ε (and this applies even in the case where the physical symmetry of the system is global
or even nonexistent; we are only worried about the invariance of the functional measure here), then
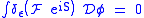
expresses the invariance of the functional measure where S is the action
and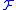
is a functional
of the fields. If the gauge transformation corresponds to a global
symmetry of the theory, then,
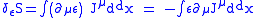
for some "current
" J (as a functional of the fields φ) after integrating by parts
and assuming that the surface terms can be neglected.
Then, the Ward-Takahashi identities become
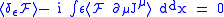
This is the QFT analog of the Noether continuity equation
.
If the gauge transformation corresponds to an actual gauge symmetry,
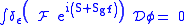
where S is the gauge invariant action and Sgf is a non-gauge-invariant gauge fixing
term.
But note that even if there is not a global symmetry (i.e. the symmetry is broken), we still have a Ward-Takahashi identity describing the rate of charge nonconservation.
If the functional measure is not gauge invariant, but happens to satisfy
where λ is some functional of the fields φ, we have an anomalous Ward-Takahashi identity. This happens when we have a chiral anomaly
, for example.
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, a Ward-Takahashi identity is an identity between correlation functions
Correlation function (quantum field theory)
In quantum field theory, the matrix element computed by inserting a product of operators between two states, usually the vacuum states, is called a correlation function....
that follows from the global or gauged symmetries
Symmetry in physics
In physics, symmetry includes all features of a physical system that exhibit the property of symmetry—that is, under certain transformations, aspects of these systems are "unchanged", according to a particular observation...
of the theory, and which remains valid after renormalization
Renormalization
In quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities....
.
The Ward-Takahashi identity of quantum electrodynamics
Quantum electrodynamics
Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
was originally used by John Clive Ward
John Clive Ward
John Clive Ward , was a British-Australian physicist. His most famous creation was the Ward-Takahashi identity, originally known as "Ward Identity" . This celebrated result, in quantum electrodynamics, was inspired by a conjecture of Dyson and was disclosed in a one-half page letter typical of...
and Yasushi Takahashi
Yasushi Takahashi
is a Japanese theoretical physicist, known for Ward-Takahashi identity. He is now professor emeritus, department of physics, University of Alberta.-Biography:*1951 B. S. Nagoya University*Fulbright Scholarships*1953 Research associate, University of Rochester...
to relate the wave function renormalization
Wave function renormalization
In quantum field theory, wave function renormalization is a rescaling, or renormalization, of quantum fields to take into account the effects of interactions. For a noninteracting or free field, the field operator creates or annihilates a single particle with probability 1. Once interactions are...
of the electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
to its vertex renormalization factor
Vertex function
In quantum electrodynamics, the vertex function describes the coupling between a photon and an electron beyond the leading order of perturbation theory...
F1(0), guaranteeing the cancellation of the ultraviolet divergence
Ultraviolet divergence
In physics, an ultraviolet divergence is a situation in which an integral, for example a Feynman diagram, diverges because of contributions of objects with very high energy , or, equivalently, because of physical phenomena at very short distances. An infinite answer to a question that should have a...
to all orders in perturbation theory. Later uses include the extension of the proof of Goldstone's theorem to all orders of perturbation theory.
The Ward-Takahashi identity is a quantum version of the classical Noether's theorem
Noether's theorem
Noether's theorem states that any differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proved by German mathematician Emmy Noether in 1915 and published in 1918...
, and any symmetries in a quantum field theory can lead to an equation of motion for correlation functions. This generalized sense should be distinguished when reading literature, such as Michael Peskin
Michael Peskin
Michael Peskin is an American theoretical physicist. He was an undergraduate at Harvard University and obtained his Ph.D. in 1978 at Cornell University studying under Kenneth Wilson. He was a Junior Fellow at the Harvard Society of Fellows from 1977–1980.He is currently a professor in the theory...
and Daniel Schroeder's textbook, An Introduction to Quantum Field Theory (see references), from the original sense of the Ward identity.
The Ward-Takahashi identity
The Ward-Takahashi identity applies to correlation functions in momentum space, which do not necessarily have all their external momenta on-shell. Let
be a QED
Quantum electrodynamics
Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
correlation function
Correlation function (quantum field theory)
In quantum field theory, the matrix element computed by inserting a product of operators between two states, usually the vacuum states, is called a correlation function....
involving an external photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
with momentum k (where
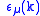is the polarizationPhoton polarization
Photon polarization is the quantum mechanical description of the classical polarized sinusoidal plane electromagnetic wave. Individual photons are completely polarized...
vector of the photon), n initial-state electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
s with momenta
, and n final-state electrons with momenta . Also define to be the simpler amplitudeProbability amplitude
In quantum mechanics, a probability amplitude is a complex number whose modulus squared represents a probability or probability density.For example, if the probability amplitude of a quantum state is \alpha, the probability of measuring that state is |\alpha|^2...
that is obtained by removing the photon with momentum k from our original amplitude. Then the Ward-Takahashi identity reads
where −e is the charge of the electron
Elementary charge
The elementary charge, usually denoted as e, is the electric charge carried by a single proton, or equivalently, the absolute value of the electric charge carried by a single electron. This elementary charge is a fundamental physical constant. To avoid confusion over its sign, e is sometimes called...
. Note that if
has its external electrons on-shell, then the amplitudes on the right-hand side of this identity each have one external particle off-shell, and therefore they do not contribute to S-matrix elements.The Ward identity
The Ward identity is a specialization of the Ward-Takahashi identity to S-matrix elements, which describe physically possible scatteringScattering
Scattering is a general physical process where some forms of radiation, such as light, sound, or moving particles, are forced to deviate from a straight trajectory by one or more localized non-uniformities in the medium through which they pass. In conventional use, this also includes deviation of...
processes and thus have all their external particles on-shell. Again let
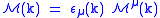be the amplitude for some QED process involving an external photon with momentum 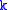, where 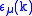is the polarizationPhoton polarization
Photon polarization is the quantum mechanical description of the classical polarized sinusoidal plane electromagnetic wave. Individual photons are completely polarized...
vector of the photon. Then the Ward identity reads:
Physically, what this identity means is the longitudinal polarization of the photon which arises in the ξ gauge is unphysical and disappears from the S-matrix.
Examples of its use include constraining the tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
structure of the vacuum polarization
Vacuum polarization
In quantum field theory, and specifically quantum electrodynamics, vacuum polarization describes a process in which a background electromagnetic field produces virtual electron–positron pairs that change the distribution of charges and currents that generated the original electromagnetic...
and of the electron vertex function
Vertex function
In quantum electrodynamics, the vertex function describes the coupling between a photon and an electron beyond the leading order of perturbation theory...
in QED.
Derivation in the path integral formulation
- See also: Path integral formulation
In the path integral formulation, the Ward-Takahashi identities are a reflection of the invariance of the functional measure under a gauge transformation. More precisely, if
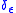represents a gauge transformation by ε (and this applies even in the case where the physical symmetry of the system is globalGlobal symmetry
A global symmetry is a symmetry that holds at all points in the spacetime under consideration, as opposed to a local symmetry which varies from point to point.Global symmetries require conservation laws, but not forces, in physics.-See also:...
or even nonexistent; we are only worried about the invariance of the functional measure here), then
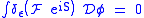
expresses the invariance of the functional measure where S is the action
Action (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
and
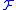is a functionalFunctional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
of the fields. If the gauge transformation corresponds to a global
Global symmetry
A global symmetry is a symmetry that holds at all points in the spacetime under consideration, as opposed to a local symmetry which varies from point to point.Global symmetries require conservation laws, but not forces, in physics.-See also:...
symmetry of the theory, then,
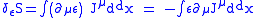
for some "current
Conserved current
In physics a conserved current is a current, j^\mu, that satisfies the continuity equation \partial_\mu j^\mu=0. The continuity equation represents a conservation law, hence the name....
" J (as a functional of the fields φ) after integrating by parts
Integration by parts
In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...
and assuming that the surface terms can be neglected.
Then, the Ward-Takahashi identities become
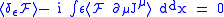
This is the QFT analog of the Noether continuity equation
.If the gauge transformation corresponds to an actual gauge symmetry,
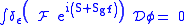
where S is the gauge invariant action and Sgf is a non-gauge-invariant gauge fixing
Gauge fixing
In the physics of gauge theories, gauge fixing denotes a mathematical procedure for coping with redundant degrees of freedom in field variables. By definition, a gauge theory represents each physically distinct configuration of the system as an equivalence class of detailed local field...
term.
But note that even if there is not a global symmetry (i.e. the symmetry is broken), we still have a Ward-Takahashi identity describing the rate of charge nonconservation.
If the functional measure is not gauge invariant, but happens to satisfy
where λ is some functional of the fields φ, we have an anomalous Ward-Takahashi identity. This happens when we have a chiral anomaly
Chiral anomaly
A chiral anomaly is the anomalous nonconservation of a chiral current. In some theories of fermions with chiral symmetry, the quantization may lead to the breaking of this chiral symmetry. In that case, the charge associated with the chiral symmetry is not conserved.The non-conservation happens...
, for example.