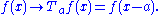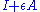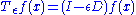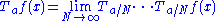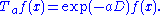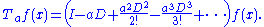Operator (physics)
Encyclopedia
In physics, an operator is a function
acting on the space of physical states. As a result
of its application on a physical state, another physical state is obtained, very often along with
some extra relevant information.
The simplest example of the utility of operators is the study of symmetry
. Because of this, they
are a very useful tool in classical mechanics
. In quantum mechanics
, on the other hand, they
are an intrinsic part of the formulation of the theory.
,
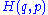function of the generalized coordinates
and its conjugate momenta. Let us consider
this function to be invariant under the action of a certain group
of transformations
, i.e., if 
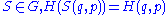. The elements of 
are physical operators, which map physical states among themselves.
An easy example is given by space translations. The hamiltonian of a translationally invariant problem does not change under the transformation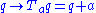
. Other straightforward symmetry operators are the ones implementing rotations.
If the physical system is described by a function, as in classical field theories, the translation operator is generalized in a straightforward way:
Notice that the transformation inside the parenthesis should be the inverse
of the transformation done on the coordinates.
where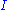
is the identity operator, 
is a small parameter, and 
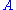will depend on the transformation at hand, and is called a generator of the group. Again, as a simple example, we will derive the generator of the space translations on 1D functions.
As it was stated,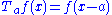
. If 
is infinitesimal, then we may write
This formula may be rewritten as
where
is the generator of the translation group, which happens to be just the derivative operator. Thus, it is said that the generator of translations is the derivative.
. In the case of the translations the idea works like this.
The translation for a finite value of
may be obtained by repeated application of the infinitesimal translation:
with the
standing for the application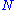 
times. If 
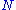is large, each of the factors may be considered to be infinitesimal:
But this limit may be rewritten as an exponential:
To be convinced of the validity of this formal expression, we may expand the exponential in a power series:
The right-hand side may be rewritten as
which is just the Taylor expansion of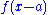
, which was our original value for 
.
The mathematical properties of physical operators are a topic of great importance in itself. For further information, see C*-algebra and Gelfand-Naimark theorem.
Physical pure states in quantum mechanics are unit-norm vectors in a certain vector space
(a Hilbert space
). Time evolution in this vector space is given by the application of a certain operator, called the evolution operator. Since the norm of the physical state should stay fixed, the evolution operator should be unitary
. Any other symmetry, mapping a physical state into another, should keep this restriction.
Any observable
, i.e., any quantity which can be measured in a physical experiment, should be associated with a self-adjoint
linear operator. The operators must yeild real eigenvalues, since they are values which may come up as the result of the experiment. Mathematically this means the operators must be Hermitian
. The probability of each eigenvalue is related to the projection of the physical state on the subspace related to that eigenvalue. See below for mathematical details.
be any linear operator for some observable A (such as position, momentum, energy, angular momentum etc), then
where a is the eigenvalue of the operator. The eigenvalue corresponds to the measured value of the observable, i.e. observable A has a measured value a. If this relation holds the wave function is said to be an eigenfunction
. If ψ is an eigenfunction, then the eigenvalue can be found and so the observable can be measured, conversely if ψ is not an eigenfunction then the eigenfunction can't be found and the observable can't be measured for that case. For a discrete basis of the eigenstates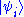
, the corresponding eigenvalues ai will also be discrete. Likewise, for a continuous basis there is a continuum of eigenstates 
and accordingly a continuum of eigenvalues a.
In bra-ket notation the above can be written;
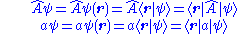
Linear operators work in any number of dimensions, that is we can have an operator acn take the form of a vector, as each component of the vector acts on the function separately due to linearity. One mathematical example is the del operator, which is itself a vector. This is useful in other quantum operators, as illustrated below.
An operator in n-dimensional space can be written:
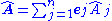
where ej are basis vectors, corresponding to each component operator Aj. Each component will yield a corresponding eigenvalue. Acting this on the wave function ψ:
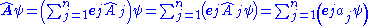
in which
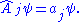
In bra-ket notation:
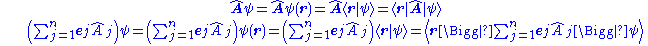
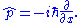
Acting on ψ obtains:
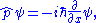
if ψ is an eigenfunction of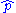
, then the momentum eigenvalue p is the value of the particle's momentum, found by:
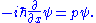
For three dimensions the momentum operator uses the nabla
operator to become:
In Cartesian coordinates (using the standard Cartesian basis vectors ex, ey, ez) this can be written;
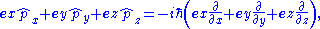
that is:
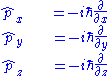
The process of finding eigenvalues is the same. Since this is a vector and operator equation, if ψ is an eigenfunction, then each component of the momentum operator will have an eigenvalue corresponding to that component of momentum. Acting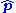
on ψ obtains:
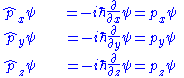
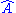and 
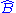, the commutator is defined by,
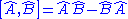
The commutator is itself a (composite) operator. Acting the commutator on ψ gives:
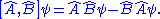
If ψ is an eigenfunction with eigenvalues a and b for observables A and B respectively, and if the operators commute:
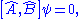
then the observables A and B can be measured at the same time with measurable eigenvalues a and b respectively. To illustrate this:
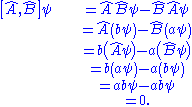
If the operators do not commute:
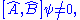
they can't be measured simultaneously to arbitrary precision, and there is an uncertainty relation between the observables, even if ψ is an eigenfunction. Notable pairs are position and momentum, and energy and time - Hiesenberg's uncertainty relations
, and the angular momenta (spin, orbital and total) about any two orthogonal axes (such as Lx and Ly, or sy and sz etc).
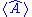of the operator 
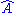is calculated from:
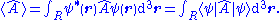
This can be generalized to any function F of an operator:
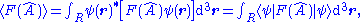
since the integrand may be manipulated as:
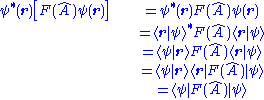
Notice in the above the product
is not an outer product, as 
multiplied by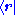 
makes ψ(r), so this freely becomes 
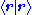and reduces to 1. An example of F is the 2-fold action of A on ψ, i.e. squaring an operator or doing it twice:
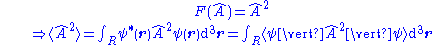
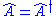
Following from this, in bra-ket notation:
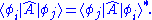
(aka transition matrix) between bases. Each basis element
can be connected to another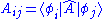 
using vector and matrix indicies ,
in which,
A further property of a hermitain operator is that eigenfunctions corresponding to different eigenvalues are orthogonal .
In matrix form, operators allow real eigenvalues to be found, corresponding to measurements. Orthogonality allows a suitable basis set of vectors to represent the state of the quantum system.
The eigenvalues of the operator are also evaluated in the same way as for the square matrix, by solving the characteristic polynomial
:
where I is the n × n identity matrix
, as an operator it corresponds to an identity operator.
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
acting on the space of physical states. As a result
of its application on a physical state, another physical state is obtained, very often along with
some extra relevant information.
The simplest example of the utility of operators is the study of symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
. Because of this, they
are a very useful tool in classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
. In quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, on the other hand, they
are an intrinsic part of the formulation of the theory.
Operators in classical mechanics
Let us consider a classical mechanics system led by a certain HamiltonianHamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
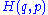,function of the generalized coordinates
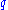and its conjugate momenta. Let us considerthis function to be invariant under the action of a certain group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of transformations
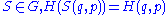, i.e., if . The elements of are physical operators, which map physical states among themselves.An easy example is given by space translations. The hamiltonian of a translationally invariant problem does not change under the transformation
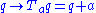. Other straightforward symmetry operators are the ones implementing rotations.If the physical system is described by a function, as in classical field theories, the translation operator is generalized in a straightforward way:
Notice that the transformation inside the parenthesis should be the inverse
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
of the transformation done on the coordinates.
Concept of generator
If the transformation is infinitesimal, the operator action should be of the form
where
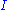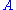is the identity operator, is a small parameter, and will depend on the transformation at hand, and is called a generator of the group. Again, as a simple example, we will derive the generator of the space translations on 1D functions.As it was stated,
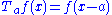. If is infinitesimal, then we may write
This formula may be rewritten as
where
is the generator of the translation group, which happens to be just the derivative operator. Thus, it is said that the generator of translations is the derivative.The exponential map
The whole group may be recovered, under normal circumstances, from the generators, via the exponential mapExponential map
In differential geometry, the exponential map is a generalization of the ordinary exponential function of mathematical analysis to all differentiable manifolds with an affine connection....
. In the case of the translations the idea works like this.
The translation for a finite value of
may be obtained by repeated application of the infinitesimal translation:
with the
standing for the application 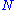times. If 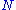is large, each of the factors may be considered to be infinitesimal:
But this limit may be rewritten as an exponential:
To be convinced of the validity of this formal expression, we may expand the exponential in a power series:
The right-hand side may be rewritten as
which is just the Taylor expansion of
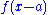, which was our original value for .The mathematical properties of physical operators are a topic of great importance in itself. For further information, see C*-algebra and Gelfand-Naimark theorem.
Operators in quantum mechanics
The mathematical description of quantum mechanics is built upon the concept of an operator.Physical pure states in quantum mechanics are unit-norm vectors in a certain vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
(a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
). Time evolution in this vector space is given by the application of a certain operator, called the evolution operator. Since the norm of the physical state should stay fixed, the evolution operator should be unitary
Unitary transformation
In mathematics, a unitary transformation may be informally defined as a transformation that respects the inner product: the inner product of two vectors before the transformation is equal to their inner product after the transformation....
. Any other symmetry, mapping a physical state into another, should keep this restriction.
Any observable
Observable
In physics, particularly in quantum physics, a system observable is a property of the system state that can be determined by some sequence of physical operations. For example, these operations might involve submitting the system to various electromagnetic fields and eventually reading a value off...
, i.e., any quantity which can be measured in a physical experiment, should be associated with a self-adjoint
Self-adjoint
In mathematics, an element x of a star-algebra is self-adjoint if x^*=x.A collection C of elements of a star-algebra is self-adjoint if it is closed under the involution operation...
linear operator. The operators must yeild real eigenvalues, since they are values which may come up as the result of the experiment. Mathematically this means the operators must be Hermitian
Hermitian
A number of mathematical entities are named Hermitian, after the mathematician Charles Hermite:*Hermitian adjoint*Hermitian connection, the unique connection on a Hermitian manifold that satisfies specific conditions...
. The probability of each eigenvalue is related to the projection of the physical state on the subspace related to that eigenvalue. See below for mathematical details.
Linear operators on a wave function
Let ψ be the wave function for a quantum system, and be any linear operator for some observable A (such as position, momentum, energy, angular momentum etc), thenwhere a is the eigenvalue of the operator. The eigenvalue corresponds to the measured value of the observable, i.e. observable A has a measured value a. If this relation holds the wave function is said to be an eigenfunction
Eigenfunction
In mathematics, an eigenfunction of a linear operator, A, defined on some function space is any non-zero function f in that space that returns from the operator exactly as is, except for a multiplicative scaling factor. More precisely, one has...
. If ψ is an eigenfunction, then the eigenvalue can be found and so the observable can be measured, conversely if ψ is not an eigenfunction then the eigenfunction can't be found and the observable can't be measured for that case. For a discrete basis of the eigenstates
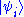, the corresponding eigenvalues ai will also be discrete. Likewise, for a continuous basis there is a continuum of eigenstates and accordingly a continuum of eigenvalues a.In bra-ket notation the above can be written;
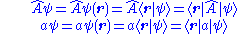
Linear operators work in any number of dimensions, that is we can have an operator acn take the form of a vector, as each component of the vector acts on the function separately due to linearity. One mathematical example is the del operator, which is itself a vector. This is useful in other quantum operators, as illustrated below.
An operator in n-dimensional space can be written:
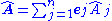
where ej are basis vectors, corresponding to each component operator Aj. Each component will yield a corresponding eigenvalue. Acting this on the wave function ψ:
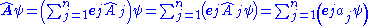
in which
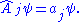
In bra-ket notation:
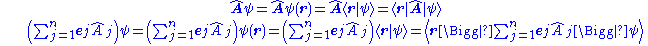
Table of QM operators
The operators used in quantum mechanics are collected in the table below (see for example,). The bold-face vectors with circumflexes are not unit vectors, they are 3-vector operators; all three spatial components taken together.| Operator (common name/s) | Component definitions | General definition | SI unit | Dimension |
|---|---|---|---|---|
| Position Position operator In quantum mechanics, the position operator is the operator that corresponds to the position observable of a particle. Consider, for example, the case of a spinless particle moving on a line. The state space for such a particle is L2, the Hilbert space of complex-valued and square-integrable ... |
   |
 |
m | [L] |
| Momentum Momentum operator In quantum mechanics, momentum is defined as an operator on the wave function. The Heisenberg uncertainty principle defines limits on how accurately the momentum and position of a single observable system can be known at once... |
   |
 |
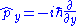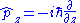J s m-1 = N s | [M] [L] [T]-1 |
| Potential energy |    |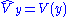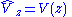
 |
J | [M] [L]2 [T]-2 |
| Energy | Time-independent:   |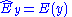
Time-Independent: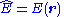 Time-Dependent:  |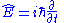
J | [M] [L]2 [T]-2 |
| Hamiltonian |  |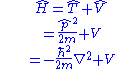
J | [M] [L]2 [T]-2 | |
| Angular momentum operator Angular momentum operator In quantum mechanics, the angular momentum operator is an operator analogous to classical angular momentum. The angular momentum operator plays a central role in the theory of atomic physics and other quantum problems involving rotational symmetry... |
   |
 |
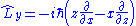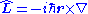J s = N s m-1 | [M] [L]2 [T]-1 |
| Spin Spin (physics) In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,... angular momentum |
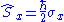   where  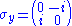  are the pauli matrices Pauli matrices The Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries... for spin-½ Spin-½ In quantum mechanics, spin is an intrinsic property of all elementary particles. Fermions, the particles that constitute ordinary matter, have half-integer spin. Spin-½ particles constitute an important subset of such fermions. All known elementary fermions have a spin of ½.- Overview :Particles... particles. |
 where σ is the vector whose components are the pauli matricies. |
J s = N s m-1 | [M] [L]2 [T]-1 |
Examples of applying quantum operators
The procedure for extracting information from a wave function is as follows. Consider the momentum p of a particle as an example. The momentum operator in one-dimension is: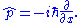Acting on ψ obtains:
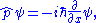
if ψ is an eigenfunction of
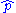, then the momentum eigenvalue p is the value of the particle's momentum, found by: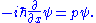For three dimensions the momentum operator uses the nabla
Nabla
Nabla may refer to one of the following:* the nabla symbol, which is used to denote the mathematical del operator where tensor is formal.* Nabla , a Hebrew stringed instrument after which that symbol was named, see harp....
operator to become:
In Cartesian coordinates (using the standard Cartesian basis vectors ex, ey, ez) this can be written;
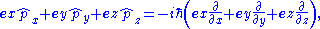
that is:
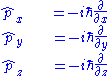
The process of finding eigenvalues is the same. Since this is a vector and operator equation, if ψ is an eigenfunction, then each component of the momentum operator will have an eigenvalue corresponding to that component of momentum. Acting
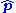on ψ obtains: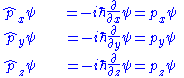Commutation of operators on Ψ
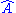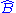If two observables A and B have linear operators and , the commutator is defined by,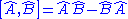The commutator is itself a (composite) operator. Acting the commutator on ψ gives:
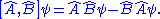
If ψ is an eigenfunction with eigenvalues a and b for observables A and B respectively, and if the operators commute:
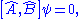
then the observables A and B can be measured at the same time with measurable eigenvalues a and b respectively. To illustrate this:
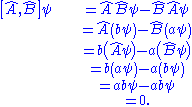
If the operators do not commute:
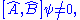
they can't be measured simultaneously to arbitrary precision, and there is an uncertainty relation between the observables, even if ψ is an eigenfunction. Notable pairs are position and momentum, and energy and time - Hiesenberg's uncertainty relations
Uncertainty principle
In quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
, and the angular momenta (spin, orbital and total) about any two orthogonal axes (such as Lx and Ly, or sy and sz etc).
Expectation values of operators on Ψ
The expectation value (equivalently the average or mean value) is the average measurement of an observable, for particle in region R. The expectation value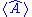 of the operator 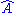is calculated from: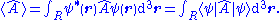This can be generalized to any function F of an operator:
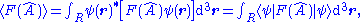
since the integrand may be manipulated as:
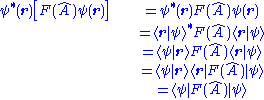
Notice in the above the product
is not an outer product, as multiplied by 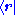makes ψ(r), so this freely becomes 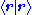and reduces to 1. An example of F is the 2-fold action of A on ψ, i.e. squaring an operator or doing it twice: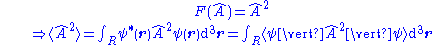Hermiticity of QM operators
The definition of a Hermitian operator is :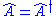Following from this, in bra-ket notation:
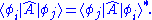
Matrix representation of quantum operators
An operator can be written in matrix form to map one basis vector to another. Since the operators and basis vectors are linear, the matrix is a linear transformationLinear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
(aka transition matrix) between bases. Each basis element
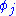can be connected to another 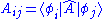using vector and matrix indicies ,in which,
A further property of a hermitain operator is that eigenfunctions corresponding to different eigenvalues are orthogonal .
In matrix form, operators allow real eigenvalues to be found, corresponding to measurements. Orthogonality allows a suitable basis set of vectors to represent the state of the quantum system.
The eigenvalues of the operator are also evaluated in the same way as for the square matrix, by solving the characteristic polynomial
Characteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
:
where I is the n × n identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
, as an operator it corresponds to an identity operator.