Theoretical and experimental justification for the Schrödinger equation
Encyclopedia
The theoretical and experimental justification for the Schrödinger equation motivates the discovery of the Schrödinger equation
, the equation that describes the dynamics of nonrelativistic particles. The motivation uses photon
s, which are relativistic particles with dynamics determined by Maxwell's equations
, as an analogue for all types of particles.
particle of light is called a photon
. Light has both a wave-like
and a particle
-like nature. In other words, light can appear to be made of photons (particles) in some experiments and light can act like waves in other experiments. The dynamics of classical electromagnetic waves are completely determined by Maxwell's equations
, the classical
description of electrodynamics. In the absence of sources, Maxwell's equations can be written as wave equation
s in the electric
and magnetic field
vectors. Maxwell's equations thus describe, among other things, the wave-like properties of light. When "classical" (coherent or thermal) light is incident on a photographic plate or CCD, the average number of "hits", "dots", or "clicks" per unit time that result is approximately proportional to the square of the electromagnetic fields of the light. By formal analogy, the wavefunction of a material particle can be used to find the probability density by taking its absolute-value squared. Unlike electromagnetic fields, quantum-mechanical wavefunctions are complex. (Often in the case of EM fields complex notation is used for convenience, but it is understood that in actual fact the fields are real. On the contrary, wavefunctions are genuinely complex.)
Maxwell's equations were completely known by the latter part of the nineteenth century. The dynamical equations for light were, therefore, well-known long before the discovery of the photon. This is not true for other particles such as the electron
. It was surmised from the interaction of light with atoms that electrons also had both a particle-like and a wave-like nature. Newtonian mechanics, a description of the particle-like behavior of macroscopic
objects, failed to describe very small objects such as electrons. Abductive reasoning
was performed to obtain the dynamics of mass
ive (particles with mass) objects such as electrons. The electromagnetic wave equation
, the equation that described the dynamics of light, was used as a prototype for discovering the Schrödinger equation
, the equation that describes the wave-like and particle-like dynamics of nonrelativistic massive particles.
or in a vacuum
. The homogeneous
form of the equation, written in terms of either the electric field
E or the magnetic field
B, takes the form:
where c is the speed of light
in the medium. In a vacuum, c = 2.998 x 108 meters per second, which is the speed of light in free space.
The magnetic field is related to the electric field through Faraday's law
(cgs units)
.
solution for an electromagnetic wave
traveling in the z direction is (cgs units and SI units)
for the electric field and
for the magnetic field, where k is the wavenumber
,
is the angular frequency
of the wave, and
is the speed of light
. The hats on the vectors indicate unit vectors in the x, y, and z directions. In complex notation
, the quantity
is the amplitude
of the wave.
Here
is the Jones vector in the x-y plane. The notation for this vector is the bra-ket notation
of Dirac
, which is normally used in a quantum context. The quantum notation is used here in anticipation of the interpretation of the Jones vector as a quantum state vector. The angles
are the angle the electric field makes with the x axis and the two initial phases of the wave, respectively.
The quantity
is the state vector of the wave. It describes the polarization of the wave
and the spatial and temporal functionality of the wave. For a coherent state
light beam so dim that its average photon number is much less than 1, this is approximately equivalent to the quantum state of a single photon.
in classical electromagnetic fields is (cgs units)
.
For a plane wave, converting to complex notation (and hence dividing by a factor of 2), this becomes
where the energy has been averaged over a wavelength of the wave.
with a similar expression for the y component.
The fraction in both components is
.
.
For a sinusoidal plane wave traveling in the z direction, the momentum is in the z direction and is related to the energy density:
.
The momentum density has been averaged over a wavelength.
.
For a sinusoidal plane wave the angular momentum is in the z direction and is given by (going over to complex notation)
where again the density is averaged over a wavelength. Here right and left circularly polarized unit vectors are defined as
and
.
or through slits
in a diffraction grating
. We can define the transformation of the state from the state at time t to the state at time
as
.
To conserve energy in the wave we require
where
is the adjoint
of U, the complex conjugate transpose of the matrix.
This implies that a transformation that conserves energy must obey
where I is the identity operator
and U is called a unitary operator
. The unitary property is necessary to ensure energy conservation
in state transformations.
is an infinitesimal real quantity 
, then the unitary transformation is very close to the identity matrix (the final state is very close to the initial state) and can be written
and the adjoint by
.
The factor of i is introduced for convenience. With this convention, it will be shown that energy conservation requires H to be a Hermitian
operator and that H is related to the energy of a particle.
Energy conservation requires
.
Since
is infinitesimal, which means that 
may be neglected
with respect to
, the last term can be omitted. Further, if H is equal to its
adjoint:
,
it follows that (for infinitesimal translations in time
)
,
so that, indeed, energy is conserved.
Operators that are equal to their adjoints are called Hermitian
or self-adjoint.
The infinitesimal translation of the polarization state is
.
Thus, energy conservation requires that infinitesimal transformations of a polarization state occur through the action of a Hermitian operator. While this derivation is classical, the concept of a Hermitian operator generating energy-conserving infinitesimal transformations forms an important basis for quantum mechanics. The derivation of the Schrödinger equation follows directly from this concept.
. However, the quantum mechanical treatment of particles follows along lines formally analogous however, to Maxwell's equations
for electrodynamics. The analog of the classical "state vectors"
in the classical description is quantum state vectors in the description of photons.
and the interpretation of those experiments by Albert Einstein
, which was that electromagnetic radiation is composed of irreducible packets of energy, known as photon
s. The energy of each packet is related to the angular frequency of the wave by the relation
where
is an experimentally determined quantity known as the reduced Planck's constant. If there are 
photons in a box of volume 
, the energy (neglecting zero point energy) in the electromagnetic field is
and the energy density is
The energy of a photon can be related to classical fields through the correspondence principle
which states that for a large number of photons, the quantum and classical treatments must agree. Thus, for very large
, the quantum energy density must be the same as the classical energy density
.
The average number of photons in the box in a coherent state is then
.
which implies that the momentum of a photon is
(or equivalently 
).
which implies that the angular momentum of the photon is
.
the quantum interpretation of this expression is that the photon has a probability of
of having an angular momentum of 
and a probability of 
of having an angular momentum of 
. We can therefore think of the angular momentum of the photon being quantized as well as the energy. This has indeed been experimentally verified. Photons have only been observed to have angular momenta of 
.
The spin
of the photon is defined as the coefficient of
in the angular momentum calculation. A photon has spin 1 if it is in the 
state and -1 if it is in the 
state. The spin operator is defined as the outer product
.
The eigenvectors of the spin operator are
and 
with eigenvalues 1 and -1, respectively.
The expected value of a spin measurement on a photon is then
.
An operator S has been associated with an observable quantity, the angular momentum. The eigenvalues of the operator are the allowed observable values. This has been demonstrated for angular momentum, but it is in general true for any observable quantity.
). The latter interpretation is the option for a single-photon Fock state
. Dirac explains this This explanation is in some sense antiquated or even obsolete, as we now know that the concept of a single-photon wavefunction is disputed http://adsabs.harvard.edu/abs/2005quant.ph..8202B, that in a coherent state
one indeed deals with the probable number of photons, given by coherent-state Poissonian statistics, and that different photons can indeed interferehttp://pra.aps.org/abstract/PRA/v49/i5/p4243_1. in the context of the double-slit experiment
:
.) The expectation value of the photon number in a coherent state in a limited region of space is quadratic in the fields. In quantum mechanics, by analogy, the state or probability amplitude
of a single particle contains the basic probability information. In general, the rules for combining probability amplitudes look very much like the classical rules for composition of probabilities: (The following quote is from Baym, Chapter 1)
In 1923 Louis de Broglie
addressed the question of whether all particles can have both a wave and a particle nature similar to the photon. Photons differ from many other particles in that they are massless and travel at the speed of light. Specifically de Broglie asked the question of whether a particle that has both a wave and a particle associated with it is consistent with Einstein's
two great 1905 contributions, the special theory of relativity
and the quantization of energy and momentum. The answer turned out to be positive. The wave and particle nature of electrons was experimentally observed
in 1927, two years after the discovery of the Schrödinger equation.
and wavenumber 
of the wave was related to the energy E and momentum p of the particle by
and
.
The question reduces to whether every observer in every inertial reference frame can agree on the phase of the wave. If so, then a wave-like description of particles may be consistent with special relativity.
and
where m is the rest mass of the particle.
This describes a wave of infinite wavelength and infinite phase velocity
.
The wave may be written as proportional to
.
This, however, is also the solution for a simple harmonic oscillator, which can be thought of as a clock in the rest frame of the particle. We can imagine a clock ticking at the same frequency as the wave is oscillating. The phases of the wave and the clock can be synchronized.
In the frame of an observer moving at relative speed v with respect to the particle, the particle clock is observed to tick at a frequency
where
is a factor that describes time dilation
of the particle clock as observed by the observer.
The phase of the observer clock is
where
is time measured in the particle frame. Both the observer clock and the particle clock agree on the phase.
The frequency and wavenumber of the wave in the observer frame is given by
and
with a phase velocity
.
The phase of the wave in the observer frame is
.
The phase of the wave in the observer frame is the same as the phase in the particle frame, as the clock in the particle frame, and the clock in the observer frame. A wave-like picture of particles is consistent with special relativity.
was unable to explain the observed behaviour of electrons in atoms. Specifically, accelerating electrons emit electromagnetic radiation according to the Larmor formula
. Electrons orbiting a nucleus should lose energy to radiation and eventually spiral into the nucleus. This is not observed. Atoms are stable on timescales much longer than predicted by the classical Larmor formula.
Also, it was noted that excited atoms emit radiation with discrete frequencies. Einstein used this fact to interpret discrete energy packets of light as, in fact, real particles. If these real particles are emitted from atoms in discrete energy packets, however, must the emitters, the electrons, also change energy in discrete energy packets? There is nothing in Newtonian mechanics that explains this.
The de Broglie hypothesis helped explain these phenomena by noting that the only allowed states for an electron orbiting an atom are those that allow for standing waves associated with each electron.
where R is known at the Rydberg constant
and is equal to 13.6 electron volts.
balances the attractive force of the electron
where m is the mass of the electron, v is the speed of the electron, r is the radius of the orbit and
where e is the charge on the electron or proton.
The energy of the orbiting electron is
which follows from the centrifugal force expression.
The angular momentum assumption of the Bohr model implies
which implies that, when combined with the centrifugal force equation, the radius of the orbit is given by
.
This implies, from the energy equation,
.
The difference between energy levels recovers the Balmer series.
If we assume that the electron has a momentum given by
as postulated by the de Broglie hypothesis, then the angular momentum is given by
where
is the wavelength of the electron wave.
If only standing electron waves are permitted in the atom then only orbits with perimeters equal to integral numbers of wavelengths are allowed:
.
This implies that allowed orbits have angular momentum
which is Bohr's fourth assumption.
Assumptions one and two immediately follow. Assumption three follows from energy conservation, which de Broglie showed was consistent with the wave interpretation of particles.
where H is a Hermitian operator determined by Maxwell's equations. The Hermiticity of the operator ensures that energy is conserved.
Erwin Schrödinger
assumed that the dynamics for massive particles were of the same form as the energy-conserving photon dynamics.
where
is the state vector for the particle and H is now an unknown Hermitian operator to be determined.
and assigned a component of the state vector to each bin
.
The subscript j identifies the bin.
.
The Hermitian condition requires
.
Schrödinger assumed that probability could only leak into adjacent bins during the small time step dt. In other words, all components of H are zero except for transitions between neighboring bins
,
.
Moreover, it is assumed that space is uniform in that all transitions to the right are equal
.
The same is true for transitions to the left
.
The transition equation becomes
.
The first term on the right side represents the movement of probability amplitude into bin j from the right. The second term represents leakage of probability from bin j to the right. The third term represents leakage of probability into bin j from the left. The fourth term represents leakage from bin j to the left. The final term represents any change of phase in the probability amplitude in bin j.
If we expand the probability amplitude to second order in the bin size
and assume space is isotropic, 
the transition equation reduces to
.
The transition equation must be consistent with the de Broglie hypothesis. In free space the probability amplitude for the de Broglie wave is proportional to
where
in the non-relativistic limit.
The de Broglie solution for free space is a solution of the transition equation if we require
and
.
The time derivative term in the transition equation can be identified with the energy of the de Broglie wave. The spatial derivative term can be identified with the kinetic energy. This suggests that the term containing
is proportional to the potential energy. This yields the Schrödinger equation
where U is the classical potential energy and
and
.
describes standing waves of energy exactly given by the Balmer series. This was a spectacular validation of the Schrödinger equation and of the wave-like nature of matter.
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
, the equation that describes the dynamics of nonrelativistic particles. The motivation uses photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
s, which are relativistic particles with dynamics determined by Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
, as an analogue for all types of particles.
- This article is at a postgraduate level. For a more general introduction to the topic see Introduction to quantum mechanicsIntroduction to quantum mechanicsQuantum mechanics is the body of scientific principles that explains the behavior of matter and its interactions with energy on the scale of atoms and atomic particles....
.
Nature of light
The quantumQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
particle of light is called a photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
. Light has both a wave-like
Wave
In physics, a wave is a disturbance that travels through space and time, accompanied by the transfer of energy.Waves travel and the wave motion transfers energy from one point to another, often with no permanent displacement of the particles of the medium—that is, with little or no associated mass...
and a particle
Elementary particle
In particle physics, an elementary particle or fundamental particle is a particle not known to have substructure; that is, it is not known to be made up of smaller particles. If an elementary particle truly has no substructure, then it is one of the basic building blocks of the universe from which...
-like nature. In other words, light can appear to be made of photons (particles) in some experiments and light can act like waves in other experiments. The dynamics of classical electromagnetic waves are completely determined by Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
, the classical
Classical physics
What "classical physics" refers to depends on the context. When discussing special relativity, it refers to the Newtonian physics which preceded relativity, i.e. the branches of physics based on principles developed before the rise of relativity and quantum mechanics...
description of electrodynamics. In the absence of sources, Maxwell's equations can be written as wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
s in the electric
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
and magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
vectors. Maxwell's equations thus describe, among other things, the wave-like properties of light. When "classical" (coherent or thermal) light is incident on a photographic plate or CCD, the average number of "hits", "dots", or "clicks" per unit time that result is approximately proportional to the square of the electromagnetic fields of the light. By formal analogy, the wavefunction of a material particle can be used to find the probability density by taking its absolute-value squared. Unlike electromagnetic fields, quantum-mechanical wavefunctions are complex. (Often in the case of EM fields complex notation is used for convenience, but it is understood that in actual fact the fields are real. On the contrary, wavefunctions are genuinely complex.)
Maxwell's equations were completely known by the latter part of the nineteenth century. The dynamical equations for light were, therefore, well-known long before the discovery of the photon. This is not true for other particles such as the electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
. It was surmised from the interaction of light with atoms that electrons also had both a particle-like and a wave-like nature. Newtonian mechanics, a description of the particle-like behavior of macroscopic
Macroscopic
The macroscopic scale is the length scale on which objects or processes are of a size which is measurable and observable by the naked eye.When applied to phenomena and abstract objects, the macroscopic scale describes existence in the world as we perceive it, often in contrast to experiences or...
objects, failed to describe very small objects such as electrons. Abductive reasoning
Abductive reasoning
Abduction is a kind of logical inference described by Charles Sanders Peirce as "guessing". The term refers to the process of arriving at an explanatory hypothesis. Peirce said that to abduce a hypothetical explanation a from an observed surprising circumstance b is to surmise that a may be true...
was performed to obtain the dynamics of mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
ive (particles with mass) objects such as electrons. The electromagnetic wave equation
Electromagnetic wave equation
The electromagnetic wave equation is a second-order partial differential equation that describes the propagation of electromagnetic waves through a medium or in a vacuum...
, the equation that described the dynamics of light, was used as a prototype for discovering the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
, the equation that describes the wave-like and particle-like dynamics of nonrelativistic massive particles.
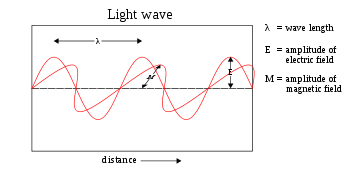
Plane sinusoidal waves
Electromagnetic wave equation
The electromagnetic wave equation describes the propagation of electromagnetic waves through a mediumMedium (optics)
An optical medium is material through which electromagnetic waves propagate. It is a form of transmission medium. The permittivity and permeability of the medium define how electromagnetic waves propagate in it...
or in a vacuum
Vacuum
In everyday usage, vacuum is a volume of space that is essentially empty of matter, such that its gaseous pressure is much less than atmospheric pressure. The word comes from the Latin term for "empty". A perfect vacuum would be one with no particles in it at all, which is impossible to achieve in...
. The homogeneous
Homogeneous differential equation
The term homogeneous differential equation has several distinct meanings.One meaning is that a first-order ordinary differential equation is homogeneous if it has the formwhere F is a homogeneous function of degree zero; that is to say, that F = F.In a related, but distinct, usage, the term linear...
form of the equation, written in terms of either the electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
E or the magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
B, takes the form:
where c is the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
in the medium. In a vacuum, c = 2.998 x 108 meters per second, which is the speed of light in free space.
The magnetic field is related to the electric field through Faraday's law
Faraday's law of induction
Faraday's law of induction dates from the 1830s, and is a basic law of electromagnetism relating to the operating principles of transformers, inductors, and many types of electrical motors and generators...
(cgs units)
.Plane wave solution of the electromagnetic wave equation
The plane sinusoidalSine wave
The sine wave or sinusoid is a mathematical function that describes a smooth repetitive oscillation. It occurs often in pure mathematics, as well as physics, signal processing, electrical engineering and many other fields...
solution for an electromagnetic wave
Electromagnetic wave equation
The electromagnetic wave equation is a second-order partial differential equation that describes the propagation of electromagnetic waves through a medium or in a vacuum...
traveling in the z direction is (cgs units and SI units)
for the magnetic field, where k is the wavenumber
Wavenumber
In the physical sciences, the wavenumber is a property of a wave, its spatial frequency, that is proportional to the reciprocal of the wavelength. It is also the magnitude of the wave vector...
,
is the angular frequency
Angular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
of the wave, and
is the speed of lightSpeed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
. The hats on the vectors indicate unit vectors in the x, y, and z directions. In complex notation
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
, the quantity
is the amplitudeAmplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
of the wave.
Here
is the Jones vector in the x-y plane. The notation for this vector is the bra-ket notation
Bra-ket notation
Bra-ket notation is a standard notation for describing quantum states in the theory of quantum mechanics composed of angle brackets and vertical bars. It can also be used to denote abstract vectors and linear functionals in mathematics...
of Dirac
Paul Dirac
Paul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
, which is normally used in a quantum context. The quantum notation is used here in anticipation of the interpretation of the Jones vector as a quantum state vector. The angles
are the angle the electric field makes with the x axis and the two initial phases of the wave, respectively.The quantity
is the state vector of the wave. It describes the polarization of the wave
Photon polarization
Photon polarization is the quantum mechanical description of the classical polarized sinusoidal plane electromagnetic wave. Individual photons are completely polarized...
and the spatial and temporal functionality of the wave. For a coherent state
Coherent state
In quantum mechanics a coherent state is a specific kind of quantum state of the quantum harmonic oscillator whose dynamics most closely resembles the oscillating behaviour of a classical harmonic oscillator...
light beam so dim that its average photon number is much less than 1, this is approximately equivalent to the quantum state of a single photon.
Energy in a plane wave
The energy per unit volumeEnergy density
Energy density is a term used for the amount of energy stored in a given system or region of space per unit volume. Often only the useful or extractable energy is quantified, which is to say that chemically inaccessible energy such as rest mass energy is ignored...
in classical electromagnetic fields is (cgs units)
.For a plane wave, converting to complex notation (and hence dividing by a factor of 2), this becomes
where the energy has been averaged over a wavelength of the wave.
Fraction of energy in each component
The fraction of energy in the x component of the plane wave (assuming linear polarization) iswith a similar expression for the y component.
The fraction in both components is
.Momentum density of classical electromagnetic waves
The momentum density is given by the Poynting vectorPoynting vector
In physics, the Poynting vector can be thought of as representing the directional energy flux density of an electromagnetic field. It is named after its inventor John Henry Poynting. Oliver Heaviside and Nikolay Umov independently co-invented the Poynting vector...
.For a sinusoidal plane wave traveling in the z direction, the momentum is in the z direction and is related to the energy density:
.The momentum density has been averaged over a wavelength.
Angular momentum density of classical electromagnetic waves
The angular momentum density is.For a sinusoidal plane wave the angular momentum is in the z direction and is given by (going over to complex notation)
where again the density is averaged over a wavelength. Here right and left circularly polarized unit vectors are defined as
and
.Unitary operators and energy conservation
A wave can be transformed by, for example, passing through a birefringent crystalBirefringence
Birefringence, or double refraction, is the decomposition of a ray of light into two rays when it passes through certain anisotropic materials, such as crystals of calcite or boron nitride. The effect was first described by the Danish scientist Rasmus Bartholin in 1669, who saw it in calcite...
or through slits
Photon dynamics in the double-slit experiment
The dynamics of photons in the double-slit experiment describes the relationship between classical electromagnetic waves and photons, the quantum counterpart of classical electromagnetic waves, in the context of the double-slit experiment....
in a diffraction grating
Diffraction grating
In optics, a diffraction grating is an optical component with a periodic structure, which splits and diffracts light into several beams travelling in different directions. The directions of these beams depend on the spacing of the grating and the wavelength of the light so that the grating acts as...
. We can define the transformation of the state from the state at time t to the state at time
as.To conserve energy in the wave we require
where
is the adjointHermitian adjoint
In mathematics, specifically in functional analysis, each linear operator on a Hilbert space has a corresponding adjoint operator.Adjoints of operators generalize conjugate transposes of square matrices to infinite-dimensional situations...
of U, the complex conjugate transpose of the matrix.
This implies that a transformation that conserves energy must obey
where I is the identity operator
Identity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
and U is called a unitary operator
Unitary operator
In functional analysis, a branch of mathematics, a unitary operator is a bounded linear operator U : H → H on a Hilbert space H satisfyingU^*U=UU^*=I...
. The unitary property is necessary to ensure energy conservation
Energy conservation
Energy conservation refers to efforts made to reduce energy consumption. Energy conservation can be achieved through increased efficient energy use, in conjunction with decreased energy consumption and/or reduced consumption from conventional energy sources...
in state transformations.
Hermitian operators and energy conservation
If is an infinitesimal real quantity , then the unitary transformation is very close to the identity matrix (the final state is very close to the initial state) and can be writtenand the adjoint by
.The factor of i is introduced for convenience. With this convention, it will be shown that energy conservation requires H to be a Hermitian
Self-adjoint operator
In mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
operator and that H is related to the energy of a particle.
Energy conservation requires
.Since
is infinitesimal, which means that may be neglectedwith respect to
, the last term can be omitted. Further, if H is equal to itsadjoint:
,it follows that (for infinitesimal translations in time
),so that, indeed, energy is conserved.
Operators that are equal to their adjoints are called Hermitian
Self-adjoint operator
In mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
or self-adjoint.
The infinitesimal translation of the polarization state is
.Thus, energy conservation requires that infinitesimal transformations of a polarization state occur through the action of a Hermitian operator. While this derivation is classical, the concept of a Hermitian operator generating energy-conserving infinitesimal transformations forms an important basis for quantum mechanics. The derivation of the Schrödinger equation follows directly from this concept.
Quantum analogy of classical electrodynamics
The treatment to this point has been classicalClassical physics
What "classical physics" refers to depends on the context. When discussing special relativity, it refers to the Newtonian physics which preceded relativity, i.e. the branches of physics based on principles developed before the rise of relativity and quantum mechanics...
. However, the quantum mechanical treatment of particles follows along lines formally analogous however, to Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
for electrodynamics. The analog of the classical "state vectors"
in the classical description is quantum state vectors in the description of photons.
Energy
The early interpretation is based on the experiments of Max PlanckMax Planck
Max Karl Ernst Ludwig Planck, ForMemRS, was a German physicist who actualized the quantum physics, initiating a revolution in natural science and philosophy. He is regarded as the founder of the quantum theory, for which he received the Nobel Prize in Physics in 1918.-Life and career:Planck came...
and the interpretation of those experiments by Albert Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
, which was that electromagnetic radiation is composed of irreducible packets of energy, known as photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
s. The energy of each packet is related to the angular frequency of the wave by the relation
where
is an experimentally determined quantity known as the reduced Planck's constant. If there are photons in a box of volume , the energy (neglecting zero point energy) in the electromagnetic field isand the energy density is
The energy of a photon can be related to classical fields through the correspondence principle
Correspondence principle
In physics, the correspondence principle states that the behavior of systems described by the theory of quantum mechanics reproduces classical physics in the limit of large quantum numbers....
which states that for a large number of photons, the quantum and classical treatments must agree. Thus, for very large
, the quantum energy density must be the same as the classical energy density.The average number of photons in the box in a coherent state is then
.Momentum
The correspondence principle also determines the momentum and angular momentum of the photon. For momentumwhich implies that the momentum of a photon is
(or equivalently ).Angular momentum and spin
Similarly for the angular momentumwhich implies that the angular momentum of the photon is
.the quantum interpretation of this expression is that the photon has a probability of
of having an angular momentum of and a probability of of having an angular momentum of . We can therefore think of the angular momentum of the photon being quantized as well as the energy. This has indeed been experimentally verified. Photons have only been observed to have angular momenta of .Spin operator
The spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
of the photon is defined as the coefficient of
in the angular momentum calculation. A photon has spin 1 if it is in the state and -1 if it is in the state. The spin operator is defined as the outer productOuter product
In linear algebra, the outer product typically refers to the tensor product of two vectors. The result of applying the outer product to a pair of vectors is a matrix...
.The eigenvectors of the spin operator are
and with eigenvalues 1 and -1, respectively.The expected value of a spin measurement on a photon is then
.An operator S has been associated with an observable quantity, the angular momentum. The eigenvalues of the operator are the allowed observable values. This has been demonstrated for angular momentum, but it is in general true for any observable quantity.
Probability for a single photon
There are two ways in which probability can be applied to the behavior of photons; probability can be used to calculate the probable number of photons in a particular state, or probability can be used to calculate the likelihood of a single photon to be in a particular state. The former interpretation is applicable to thermal or to coherent light (see Quantum opticsQuantum optics
Quantum optics is a field of research in physics, dealing with the application of quantum mechanics to phenomena involving light and its interactions with matter.- History of quantum optics :...
). The latter interpretation is the option for a single-photon Fock state
Fock state
A Fock state , in quantum mechanics, is any element of a Fock space with a well-defined number of particles . These states are named after the Soviet physicist, V. A. Fock.-Definition:...
. Dirac explains this This explanation is in some sense antiquated or even obsolete, as we now know that the concept of a single-photon wavefunction is disputed http://adsabs.harvard.edu/abs/2005quant.ph..8202B, that in a coherent state
Coherent state
In quantum mechanics a coherent state is a specific kind of quantum state of the quantum harmonic oscillator whose dynamics most closely resembles the oscillating behaviour of a classical harmonic oscillator...
one indeed deals with the probable number of photons, given by coherent-state Poissonian statistics, and that different photons can indeed interferehttp://pra.aps.org/abstract/PRA/v49/i5/p4243_1. in the context of the double-slit experiment
Double-slit experiment
The double-slit experiment, sometimes called Young's experiment, is a demonstration that matter and energy can display characteristics of both waves and particles...
:
Probability amplitudes
The probability for a photon to be in a particular polarization state depends on the probability distribution over the fields as calculated by the classical Maxwell's equations (in the Glauber-Sudarshan P-representation of a one-photon Fock stateFock state
A Fock state , in quantum mechanics, is any element of a Fock space with a well-defined number of particles . These states are named after the Soviet physicist, V. A. Fock.-Definition:...
.) The expectation value of the photon number in a coherent state in a limited region of space is quadratic in the fields. In quantum mechanics, by analogy, the state or probability amplitude
Probability amplitude
In quantum mechanics, a probability amplitude is a complex number whose modulus squared represents a probability or probability density.For example, if the probability amplitude of a quantum state is \alpha, the probability of measuring that state is |\alpha|^2...
of a single particle contains the basic probability information. In general, the rules for combining probability amplitudes look very much like the classical rules for composition of probabilities: (The following quote is from Baym, Chapter 1)
- The probability amplitude for two successive probabilities is the product of amplitudes for the individual possibilities. ...
- The amplitude for a process that can take place in one of several indistinguishable ways is the sum of amplitudes for each of the individual ways. ...
- The total probability for the process to occur is the absolute value squared of the total amplitude calculated by 1 and 2.
de Broglie waves
Louis, 7th duc de Broglie
Louis-Victor-Pierre-Raymond, 7th duc de Broglie, FRS was a French physicist and a Nobel laureate in the year 1929. He was the sixteenth member elected to occupy seat 1 of the Académie française in 1944, and served as Perpetual Secretary of the Académie des sciences, France.-Biography :Louis de...
addressed the question of whether all particles can have both a wave and a particle nature similar to the photon. Photons differ from many other particles in that they are massless and travel at the speed of light. Specifically de Broglie asked the question of whether a particle that has both a wave and a particle associated with it is consistent with Einstein's
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
two great 1905 contributions, the special theory of relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
and the quantization of energy and momentum. The answer turned out to be positive. The wave and particle nature of electrons was experimentally observed
Davisson-Germer experiment
The Davisson–Germer experiment was a physics experiment conducted by American physicists Clinton Davisson and Lester Germer in 1927, which confirmed the de Broglie hypothesis. This hypothesis advanced by Louis de Broglie in 1924 says that particles of matter such as electrons have wave like...
in 1927, two years after the discovery of the Schrödinger equation.
de Broglie hypothesis
De Broglie supposed that every particle was associated with both a particle and a wave. The angular frequency and wavenumber of the wave was related to the energy E and momentum p of the particle byand
.The question reduces to whether every observer in every inertial reference frame can agree on the phase of the wave. If so, then a wave-like description of particles may be consistent with special relativity.
Rest frame
First consider the rest frame of the particle. In that case the frequency and wavenumber of the wave are related to the energy and momentum of the particles properties byand
where m is the rest mass of the particle.
This describes a wave of infinite wavelength and infinite phase velocity
Phase velocity
The phase velocity of a wave is the rate at which the phase of the wave propagates in space. This is the speed at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave will appear to travel at the phase velocity...
.The wave may be written as proportional to
.This, however, is also the solution for a simple harmonic oscillator, which can be thought of as a clock in the rest frame of the particle. We can imagine a clock ticking at the same frequency as the wave is oscillating. The phases of the wave and the clock can be synchronized.
Frame of the observer
It is shown that the phase of the wave in an observer frame is the same as the phase of the wave in a particle frame, and also the same as clocks in the two frames. There is, therefore, consistency of both a wave-like and a particle-like picture in special relativity.Phase of the observer clock
In the frame of an observer moving at relative speed v with respect to the particle, the particle clock is observed to tick at a frequency
where
is a factor that describes time dilation
Time dilation
In the theory of relativity, time dilation is an observed difference of elapsed time between two events as measured by observers either moving relative to each other or differently situated from gravitational masses. An accurate clock at rest with respect to one observer may be measured to tick at...
of the particle clock as observed by the observer.
The phase of the observer clock is
where
is time measured in the particle frame. Both the observer clock and the particle clock agree on the phase.Phase of the observer wave
The frequency and wavenumber of the wave in the observer frame is given by
and
with a phase velocity
.The phase of the wave in the observer frame is
.The phase of the wave in the observer frame is the same as the phase in the particle frame, as the clock in the particle frame, and the clock in the observer frame. A wave-like picture of particles is consistent with special relativity.
Bohr atom
Inconsistency of observation with classical physics
The de Broglie hypothesis helped resolve outstanding issues in atomic physics. Classical physicsClassical physics
What "classical physics" refers to depends on the context. When discussing special relativity, it refers to the Newtonian physics which preceded relativity, i.e. the branches of physics based on principles developed before the rise of relativity and quantum mechanics...
was unable to explain the observed behaviour of electrons in atoms. Specifically, accelerating electrons emit electromagnetic radiation according to the Larmor formula
Larmor formula
In physics, in the area of electrodynamics, the Larmor formula is used to calculate the total power radiated by a nonrelativistic point charge as it accelerates. It was first derived by J. J...
. Electrons orbiting a nucleus should lose energy to radiation and eventually spiral into the nucleus. This is not observed. Atoms are stable on timescales much longer than predicted by the classical Larmor formula.
Also, it was noted that excited atoms emit radiation with discrete frequencies. Einstein used this fact to interpret discrete energy packets of light as, in fact, real particles. If these real particles are emitted from atoms in discrete energy packets, however, must the emitters, the electrons, also change energy in discrete energy packets? There is nothing in Newtonian mechanics that explains this.
The de Broglie hypothesis helped explain these phenomena by noting that the only allowed states for an electron orbiting an atom are those that allow for standing waves associated with each electron.
Balmer series
The Balmer series identifies those frequencies of light that can be emitted from an excited hydrogen atom:where R is known at the Rydberg constant
Rydberg constant
The Rydberg constant, symbol R∞, named after the Swedish physicist Johannes Rydberg, is a physical constant relating to atomic spectra in the science of spectroscopy. Rydberg initially determined its value empirically from spectroscopy, but Niels Bohr later showed that its value could be calculated...
and is equal to 13.6 electron volts.
Assumptions of the Bohr model
The Bohr model, introduced in 1913, was an attempt to provide a theoretical basis for the Balmer series. The assumptions of the model are:- The orbiting electrons existed in circular orbits that had discrete quantizedQuantization (physics)In physics, quantization is the process of explaining a classical understanding of physical phenomena in terms of a newer understanding known as "quantum mechanics". It is a procedure for constructing a quantum field theory starting from a classical field theory. This is a generalization of the...
energies. That is, not every orbit is possible but only certain specific ones. - The laws of classical mechanicsClassical mechanicsIn physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
do not apply when electrons make the jump from one allowed orbit to another. - When an electron makes a jump from one orbit to another the energy difference is carried off (or supplied) by a single quantum of light (called a photonPhotonIn physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
) which has an energy equal to the energy difference between the two orbitals. - The allowed orbits depend on quantized (discrete) values of orbital angular momentumAngular momentumIn physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
, L according to the equation
Where n = 1,2,3,… and is called the principal quantum numberPrincipal quantum numberIn atomic physics, the principal quantum symbolized as n is the firstof a set of quantum numbers of an atomic orbital. The principal quantum number can only have positive integer values...
.
Implications of the Bohr model
In a circular orbit the centrifugal forceCentrifugal force
Centrifugal force can generally be any force directed outward relative to some origin. More particularly, in classical mechanics, the centrifugal force is an outward force which arises when describing the motion of objects in a rotating reference frame...
balances the attractive force of the electron
where m is the mass of the electron, v is the speed of the electron, r is the radius of the orbit and
where e is the charge on the electron or proton.
The energy of the orbiting electron is
which follows from the centrifugal force expression.
The angular momentum assumption of the Bohr model implies
which implies that, when combined with the centrifugal force equation, the radius of the orbit is given by
.This implies, from the energy equation,
.The difference between energy levels recovers the Balmer series.
De Broglie's contribution to the Bohr model
The Bohr assumptions recover the observed Balmer series. The Bohr assumptions themselves, however, are not based on any more general theory. Why, for instance, should the allowed orbits depend on the angular momentum? The de Broglie hypothesis provides some insight.If we assume that the electron has a momentum given by
as postulated by the de Broglie hypothesis, then the angular momentum is given by
where
is the wavelength of the electron wave.If only standing electron waves are permitted in the atom then only orbits with perimeters equal to integral numbers of wavelengths are allowed:
.This implies that allowed orbits have angular momentum
which is Bohr's fourth assumption.
Assumptions one and two immediately follow. Assumption three follows from energy conservation, which de Broglie showed was consistent with the wave interpretation of particles.
Need for dynamical equations
The problem with the de Broglie hypothesis as applied to the Bohr atom is that we have forced a plane wave solution valid in empty space to a situation in which there is a strong attractive potential. We have not yet discovered the general dynamic equation for the evolution of electron waves. The Schrödinger equation is the immediate generalization of the de Broglie hypothesis and the dynamics of the photon.Analogy with photon dynamics
The dynamics of a photon is given bywhere H is a Hermitian operator determined by Maxwell's equations. The Hermiticity of the operator ensures that energy is conserved.
Erwin Schrödinger
Erwin Schrödinger
Erwin Rudolf Josef Alexander Schrödinger was an Austrian physicist and theoretical biologist who was one of the fathers of quantum mechanics, and is famed for a number of important contributions to physics, especially the Schrödinger equation, for which he received the Nobel Prize in Physics in 1933...
assumed that the dynamics for massive particles were of the same form as the energy-conserving photon dynamics.
where
is the state vector for the particle and H is now an unknown Hermitian operator to be determined.Particle state vector
Rather than polarization states as in the photon case, Schrödinger assumed the state of the vector depended on the position of the particle. If a particle lives in one spatial dimension, then he divided the line up into an infinite number of small bins of length and assigned a component of the state vector to each bin.The subscript j identifies the bin.
Matrix form and transition amplitudes
The transition equation can be written in matrix form as.The Hermitian condition requires
.Schrödinger assumed that probability could only leak into adjacent bins during the small time step dt. In other words, all components of H are zero except for transitions between neighboring bins
,.Moreover, it is assumed that space is uniform in that all transitions to the right are equal
.The same is true for transitions to the left
.The transition equation becomes
.The first term on the right side represents the movement of probability amplitude into bin j from the right. The second term represents leakage of probability from bin j to the right. The third term represents leakage of probability into bin j from the left. The fourth term represents leakage from bin j to the left. The final term represents any change of phase in the probability amplitude in bin j.
If we expand the probability amplitude to second order in the bin size
and assume space is isotropic, the transition equation reduces to.Schrödinger equation in one dimension
where
in the non-relativistic limit.
The de Broglie solution for free space is a solution of the transition equation if we require
and
.The time derivative term in the transition equation can be identified with the energy of the de Broglie wave. The spatial derivative term can be identified with the kinetic energy. This suggests that the term containing
is proportional to the potential energy. This yields the Schrödinger equationwhere U is the classical potential energy and
and
.Schrödinger equation in three dimensions
In three dimensions the Schrödinger equation becomesHydrogen atom
The solution for the hydrogen atomHydrogen atom
A hydrogen atom is an atom of the chemical element hydrogen. The electrically neutral atom contains a single positively-charged proton and a single negatively-charged electron bound to the nucleus by the Coulomb force...
describes standing waves of energy exactly given by the Balmer series. This was a spectacular validation of the Schrödinger equation and of the wave-like nature of matter.
See also
- Basic concepts of quantum mechanicsBasic concepts of quantum mechanicsQuantum mechanics explains the behaviour of matter and energy on the scale of atoms and subatomic particles.Classical physics explains matter and energy at the macroscopic level of the scale familiar to human experience, including the behavior of astronomical bodies...
- Dirac equationDirac equationThe Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and...
- Path integral formulationPath integral formulationThe path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics...
- Photoelectric effectPhotoelectric effectIn the photoelectric effect, electrons are emitted from matter as a consequence of their absorption of energy from electromagnetic radiation of very short wavelength, such as visible or ultraviolet light. Electrons emitted in this manner may be referred to as photoelectrons...
- Photon dynamics in the double-slit experimentPhoton dynamics in the double-slit experimentThe dynamics of photons in the double-slit experiment describes the relationship between classical electromagnetic waves and photons, the quantum counterpart of classical electromagnetic waves, in the context of the double-slit experiment....
- Photon polarizationPhoton polarizationPhoton polarization is the quantum mechanical description of the classical polarized sinusoidal plane electromagnetic wave. Individual photons are completely polarized...
- Quantum electrodynamicsQuantum electrodynamicsQuantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
- Relation between Schrödinger's equation and the path integral formulation of quantum mechanicsRelation between Schrödinger's equation and the path integral formulation of quantum mechanicsThis article relates the Schrödinger equation with the path integral formulation of quantum mechanics using a simple nonrelativistic one-dimensional single-particle Hamiltonian composed of kinetic and potential energy.-Schrödinger's equation:...
- Stern–Gerlach experimentStern–Gerlach experimentImportant in the field of quantum mechanics, the Stern–Gerlach experiment, named after Otto Stern and Walther Gerlach, is a 1922 experiment on the deflection of particles, often used to illustrate basic principles of quantum mechanics...
- Wave-particle duality