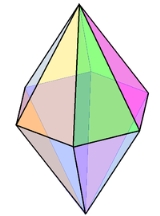
Bipyramid
Encyclopedia
| Set of bipyramids | |
|---|---|
 (Example hexagonal form) |
|
| Faces | 2n triangle Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... s |
| Edges | 3n |
| Vertices | n + 2 |
| Face configuration Face configuration In geometry, a face configuration is notational description of a face-transitive polyhedron. It represents a sequential count of the number of faces that exist at each vertex around a face.... |
V4.4.n |
| Symmetry group | Dnh, [n,2], (*22n) |
| Dual polyhedron Dual polyhedron In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another... |
n-gonal prism Prism (geometry) In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a... |
| Properties | convex, face-transitive |
| Net Net (polyhedron) In geometry the net of a polyhedron is an arrangement of edge-joined polygons in the plane which can be folded to become the faces of the polyhedron... |
 |
An n-gonal bipyramid or dipyramid is a polyhedron
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
formed by joining an n-gonal pyramid
Pyramid (geometry)
In geometry, a pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex. Each base edge and apex form a triangle. It is a conic solid with polygonal base....
and its mirror image
Mirror image
A mirror image is a reflected duplication of an object that appears identical but reversed. As an optical effect it results from reflection off of substances such as a mirror or water. It is also a concept in geometry and can be used as a conceptualization process for 3-D structures...
base-to-base.
The referenced n-gon in the name of the bipyramids is not an external face but an internal one, existing on the primary symmetry plane which connects the two pyramid halves.
The face-transitive bipyramids are the dual polyhedra
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
of the uniform prisms
Prism (geometry)
In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
and will generally have isosceles triangle faces.
A bipyramid can be projected on a sphere or globe
Globe
A globe is a three-dimensional scale model of Earth or other spheroid celestial body such as a planet, star, or moon...
as n equally spaced lines of longitude
Longitude
Longitude is a geographic coordinate that specifies the east-west position of a point on the Earth's surface. It is an angular measurement, usually expressed in degrees, minutes and seconds, and denoted by the Greek letter lambda ....
going from pole
Geographical pole
A geographical pole is either of the two points—the north pole and the south pole—on the surface of a rotating planet where the axis of rotation meets the surface of the body...
to pole, and bisected
Bisection
In geometry, bisection is the division of something into two equal or congruent parts, usually by a line, which is then called a bisector. The most often considered types of bisectors are the segment bisector and the angle bisector In geometry, bisection is the division of something into two equal...
by a line around the equator
Equator
An equator is the intersection of a sphere's surface with the plane perpendicular to the sphere's axis of rotation and containing the sphere's center of mass....
.
Bipyramid face
Face (geometry)
In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...
s, projected as spherical triangles, represent the fundamental domains in the dihedral symmetry Dnh.
Volume
The volumeVolume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
of a bipyramid is
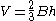where B is the area of the base and h the height from the base to the apex. This works for any location of the apex, provided that h is measured as the perpendicularPerpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
distance from the plane which contains the base.
The volume of a bipyramid whose base is a regular n-sided polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
with side length s and whose height is h is therefore:
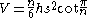
Equilateral triangle bipyramids
Only three kinds of bipyramids can have all edges of the same length (which implies that all faces are equilateral triangles, and thus the bipyramid is a deltahedronDeltahedron
A deltahedron is a polyhedron whose faces are all equilateral triangles. The name is taken from the Greek majuscule delta , which has the shape of an equilateral triangle. There are infinitely many deltahedra, but of these only eight are convex, having 4, 6, 8, 10, 12, 14, 16 and 20 faces...
): the triangular
Triangular dipyramid
In geometry, the triangular bipyramid is the first in the infinite set of face-transitive bipyramids. It is the dual of the triangular prism with 6 isosceles triangle faces....
, tetragonal, and pentagonal
Pentagonal dipyramid
In geometry, the pentagonal bipyramid is third of the infinite set of face-transitive bipyramids.Each bipyramid is the dual of a uniform prism.If the faces are equilateral triangles, it is a deltahedron and a Johnson solid...
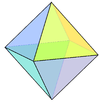
bipyramids. The tetragonal bipyramid with identical edges, or regular octahedron, counts among the Platonic solid
Platonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
s, while the triangular and pentagonal bipyramids with identical edges count among the Johnson solid
Johnson solid
In geometry, a Johnson solid is a strictly convex polyhedron, each face of which is a regular polygon, but which is not uniform, i.e., not a Platonic solid, Archimedean solid, prism or antiprism. There is no requirement that each face must be the same polygon, or that the same polygons join around...
s (J12 and J13).
 |
 |
 |
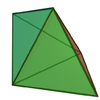
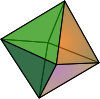
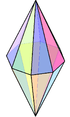
| Triangular bipyramid | Square bipyramid (Octahedron Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... ) |
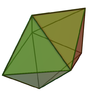
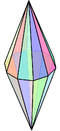
Pentagonal bipyramid |
Forms
- Triangular bipyramid - 6 faces - dual triangular prismTriangular prismIn geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides....
- Square bipyramid (the regular octahedron is a special case) - 8 faces - dual cubeCubeIn geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
- Pentagonal bipyramid - 10 faces - dual pentagonal prismPentagonal prismIn geometry, the pentagonal prism is a prism with a pentagonal base. It is a type of heptahedron with 7 faces, 15 edges, and 10 vertices.- As a semiregular polyhedron :...
- Hexagonal bipyramidHexagonal bipyramidA hexagonal bipyramid is a polyhedron formed from two hexagonal pyramids joined at their bases. The resulting solid has 12 triangular faces, 8 vertices and 18 edges. The 12 faces are identical isosceles triangles.It is one of an infinite set of bipyramids...
- 12 faces - dual hexagonal prismHexagonal prismIn geometry, the hexagonal prism is a prism with hexagonal base. The shape has 8 faces, 18 edges, and 12 vertices.Since it has eight faces, it is an octahedron. However, the term octahedron is primarily used to refer to the regular octahedron, which has eight triangular faces... - Heptagonal bipyramid - 14 faces - dual heptagonal prismHeptagonal prismIn geometry, the heptagonal prism is the fifth of the infinite set of convex prisms formed by square sides and two regular polygon caps, in this case two heptagons....
- Octagonal bipyramidOctagonal bipyramidThe octagonal bipyramid is one of the infinite set of bipyramids, dual to the infinite prisms. If an octagonal bipyramid is to be face-transitive, all faces must be isosceles triangles...
- 16 faces - dual octagonal prismOctagonal prismIn geometry, the octagonal prism is the sixth in an infinite set of prisms, formed by square sides and two regular octagon caps.If faces are all regular, it is a semiregular polyhedron.- Use :... - Enneagonal bipyramid - 18 faces - dual enneagonal prism
- Decagonal bipyramidDecagonal bipyramidIn geometry, a decagonal bipyramid is one of the infinite set of bipyramids, dual to the infinite prisms. If a decagonal bipyramid is to be face-transitive, all faces must be isosceles triangles...
- 20 faces - dual decagonal prismDecagonal prismIn geometry, the decagonal prism is the eighth in an infinite set of prisms, formed by ten square side faces and two regular decagon caps. With twelve faces, it is one of many nonregular dodecahedra.If faces are all regular, it is a semiregular polyhedron....
- ...n-gonal bipyramid - 2n faces - dual n-gonal prismPrism (geometry)In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
- ...n-gonal bipyramid - 2n faces - dual n-gonal prism
 3 |
 4 |
5 |
6 |
 8 |
 10 |
Symmetry groups
If the base is regular and the line through the apexesApex (geometry)
In geometry, an apex is the vertex which is in some sense the highest of the figure to which it belongs.*In an isosceles triangle, the apex is the vertex where the two sides of equal length meet, opposite the unequal third side....
intersects the base at its center, the symmetry group of the n-agonal bipyramid has dihedral symmetry
Dihedral symmetry in three dimensions
This article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:...
Dnh of order 4n, except in the case of a regular octahedron, which has the larger octahedral symmetry
Octahedral symmetry
150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation...
group Oh of order 48, which has three versions of D4h as subgroups.
The rotation group
Rotation group
In mechanics and geometry, the rotation group is the group of all rotations about the origin of three-dimensional Euclidean space R3 under the operation of composition. By definition, a rotation about the origin is a linear transformation that preserves length of vectors and preserves orientation ...
is Dn of order 2n, except in the case of a regular octahedron, which has the larger symmetry group O of order 24, which has three versions of D4 as subgroups.
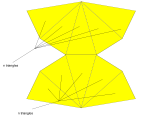
Star bipyramids
Self-intersecting bipyramids exist with a star polygon central figure, defined by triangular faces connecting each polygon edge to these two points.For example, a pentagrammic dipyramid is an isohedral star polyhedron
Star polyhedron
In geometry, a star polyhedron is a polyhedron which has some repetitive quality of nonconvexity giving it a star-like visual quality.There are two general kinds of star polyhedron:*Polyhedra which self-intersect in a repetitive way....
composed of 10 intersecting isoceles triangles. It is the dual
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
to the pentagrammic prism
Pentagrammic prism
In geometry, the pentagrammic prism is one in an infinite set of nonconvex prisms formed by square sides and two regular star polygon caps, in this case two pentagrams.This polyhedron is identified with the indexed name U78 as a uniform polyhedron....
.
Higher dimensions
In general, a bipyramid can be seen as an n-polytopePolytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
constructed with a (n-1)-polytope in a hyperplane
Hyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
with two points in opposite directions, equal distance perpendicular from the hyperplane. If the (n-1)-polytope is a regular polytope, it will have identical pyramids
Pyramid (geometry)
In geometry, a pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex. Each base edge and apex form a triangle. It is a conic solid with polygonal base....
facets.
External links
- The Uniform Polyhedra
- Virtual Reality Polyhedra The Encyclopedia of Polyhedra
- VRMLVRMLVRML is a standard file format for representing 3-dimensional interactive vector graphics, designed particularly with the World Wide Web in mind...
models (George Hart) <3> <4> <5> <6> <7> <8> <9> <10>- Conway Notation for Polyhedra Try: "dPn", where n = 3, 4, 5, 6, ... example "dP4" is an octahedron.
- VRML