
Octahedral symmetry
Encyclopedia

Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
has 24 rotational (or orientation-preserving) symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation. A cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
has the same set of symmetries, since it is the dual
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
of an octahedron.
The group of orientation-preserving symmetries is S4, the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
or the group of permutations of four objects, since there is exactly one such symmetry for each permutation of the four pairs of opposite sides of the octahedron.
Details

Point groups in three dimensions
In geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O, the group of all isometries that leave the origin fixed, or correspondingly, the group...
(or equivalently, symmetries on the sphere) with the largest symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
s compatible with translational symmetry
Translational symmetry
In geometry, a translation "slides" an object by a a: Ta = p + a.In physics and mathematics, continuous translational symmetry is the invariance of a system of equations under any translation...
. They are among the crystallographic point groups of the cubic crystal system.
Chiral octahedral symmetry
O, 432, or [4,3]+ of order 24, is chiral octahedral symmetry or rotational octahedral symmetry . This group is like chiral tetrahedral symmetryTetrahedral symmetry
150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
T, but the C2 axes are now C4 axes, and additionally there are 6 C2 axes, through the midpoints of the edges of the cube. Td and O are isomorphic as abstract groups: they both correspond to S4, the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
on 4 objects. Td is the union of T and the set obtained by combining each element of O \ T with inversion. O is the rotation group of the cube and the regular octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
.
Subgroups
- O and T
- D4, D3 and D2
- C4, C3 and C2
- E
Conjugacy classes
- identity
- 6 × rotation by 90°
- 8 × rotation by 120°
- 3 × rotation by 180° about a 4-fold axis
- 6 × rotation by 180° about a 2-fold axis
Achiral octahedral symmetry
- Oh, *432, [4,3]+, or m3m of order 48 - achiral octahedral symmetry or full octahedral symmetry. This group has the same rotation axes as O, but with mirror planes, comprising both the mirror planes of Td and Th. This group is isomorphic to S4 × C2, and is the full symmetry group of the cube and octahedronOctahedronIn geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
. It is the hyperoctahedral groupHyperoctahedral groupIn mathematics, a hyperoctahedral group is an important type of group that can be realized as the group of symmetries of a hypercube or of a cross-polytope. Groups of this type are identified by a parameter n, the dimension of the hypercube....
for n = 3. See also the isometries of the cube.
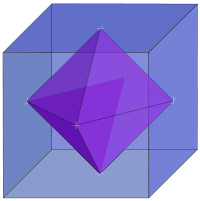
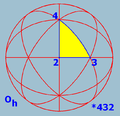
With the 4-fold axes as coordinate axes, a fundamental domain of Oh is given by 0 ≤ x ≤ y ≤ z. An object with this symmetry is characterized by the part of the object in the fundamental domain, for example the cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
is given by z = 1, and the octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
by x + y + z = 1 (or the corresponding inequalities, to get the solid instead of the surface).
ax + by + cz = 1 gives a polyhedron with 48 faces, e.g. the disdyakis dodecahedron.
Faces are 8-by-8 combined to larger faces for a = b = 0 (cube) and 6-by-6 for a = b = c (octahedron).
Subgroups
- Oh
- O, Th, Td and T
- D4h and D2h
- D3d and D2d
- D4, D3 and D2
- C4h, C3h and C2h
- C4v, C3v and C2v
- C4, C3 and C2
- S6, S4 and S2=Ci
- E and Cs
Conjugacy classes
- inversion
- 6 × rotoreflection by 90°
- 8 × rotoreflection by 60°
- 3 × reflection in a plane perpendicular to a 4-fold axis
- 6 × reflection in a plane perpendicular to a 2-fold axis
The isometries of the cube
(To be integrated in the rest of the text.)The cube has 48 isometries, forming the symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
Oh, isomorphic to S4
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
× C2. They can be categorized as follows:
- O (the identity and 23 proper rotations) with the following conjugacy classConjugacy classIn mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
es (in parentheses are given the permutations of the body diagonals and the unit quaternion representationQuaternions and spatial rotationUnit quaternions provide a convenient mathematical notation for representing orientations and rotations of objects in three dimensions. Compared to Euler angles they are simpler to compose and avoid the problem of gimbal lock. Compared to rotation matrices they are more numerically stable and may...
):- identity (identity; 1)
- rotation about an axis from the center of a face to the center of the opposite face by an angle of 90°: 3 axes, 2 per axis, together 6 ((1 2 3 4), etc.; ((1±i)/√2, etc.)
- ditto by an angle of 180°: 3 axes, 1 per axis, together 3 ((1 2)(3 4), etc.; i,j,k)
- rotation about an axis from the center of an edge to the center of the opposite edge by an angle of 180°: 6 axes, 1 per axis, together 6 ((1 2), etc.; ((i±j)/√2, etc.)
- rotation about a body diagonal by an angle of 120°: 4 axes, 2 per axis, together 8 ((1 2 3), etc.; (1±i±j±k)/2)
- The same with inversion (x is mapped to −x) (also 24 isometries). Note that rotation by an angle of 180° about an axis combined with inversion is just reflection in the perpendicular plane. The combination of inversion and rotation about a body diagonal by an angle of 120° is rotation about the body diagonal by an angle of 60°, combined with reflection in the perpendicular plane (the rotation itself does not map the cube to itself; the intersection of the reflection plane with the cube is a regular hexagon).
An isometry of the cube can be identified in various ways:
- by the faces three given adjacent faces (say 1, 2, and 3 on a die) are mapped to
- by the image of a cube with on one face a non-symmetric marking: the face with the marking, whether it is normal or a mirror image, and the orientation
- by a permutation of the four body diagonals (each of the 24 permutations is possible), combined with a toggle for inversion of the cube, or not
For cubes with colors or markings (like dice
Dice
A die is a small throwable object with multiple resting positions, used for generating random numbers...
have), the symmetry group is a subgroup of Oh. Examples:
- C4v: if one face has a different color (or two opposite faces have colors different from each other and from the other four), the cube has 8 isometries, like a square has in 2D.
- D2h: if opposite faces have the same colors, different for each set of two, the cube has 8 isometries, like a cuboidCuboidIn geometry, a cuboid is a solid figure bounded by six faces, forming a convex polyhedron. There are two competing definitions of a cuboid in mathematical literature...
. - D4h: if two opposite faces have the same color, and all other faces have one different color, the cube has 16 isometries, like a square prismPrism (geometry)In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
(square box). - C2v:
- if two adjacent faces have the same color, and all other faces have one different color, the cube has 4 isometries.
- if three faces, of which two opposite to each other, have one color and the other three one other color, the cube has 4 isometries.
- if two opposite faces have the same color, and two other opposite faces also, and the last two have different colors, the cube has 4 isometries, like a piece of blank paper with a shape with a mirror symmetry.
- Cs:
- if two adjacent faces have colors different from each other, and the other four have a third color, the cube has 2 isometries.
- if two opposite faces have the same color, and all other faces have different colors, the cube has 2 isometries, like an asymmetric piece of blank paper.
- C3v: if three faces, of which none opposite to each other, have one color and the other three one other color, the cube has 6 isometries.
For some larger subgroups a cube with that group as symmetry group is not possible with just coloring whole faces. One has to draw some pattern on the faces. Examples:
- D2d: if one face has a line segment dividing the face into two equal rectangles, and the opposite has the same in perpendicular direction, the cube has 8 isometries; there is a symmetry plane and 2-fold rotational symmetry with an axis at an angle of 45° to that plane, and, as a result, there is also another symmetry plane perpendicular to the first, and another axis of 2-fold rotational symmetry perpendicular to the first.
- Th: if each face has a line segment dividing the face into two equal rectangles, such that the line segments of adjacent faces do not meet at the edge, the cube has 24 isometries: the even permutations of the body diagonals and the same combined with inversion (x is mapped to −x).
- Td: if the cube consists of eight smaller cubes, four white and four black, put together alternatingly in all three standard directions, the cube has again 24 isometries: this time the even permutations of the body diagonals and the inverses of the other proper rotations.
- T: if each face has the same pattern with 2-fold rotational symmetry, say the letter S, such that at all edges a top of one S meets a side of the other S, the cube has 12 isometries: the even permutations of the body diagonals.
The full symmetry of the cube (Oh) is preserved if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
all faces have the same pattern such that the full symmetry of the square is preserved, with for the square a symmetry group of order 8.
The full symmetry of the cube under proper rotations (O) is preserved if and only if all faces have the same pattern with 4-fold rotational symmetry.
Octahedral symmetry of the Bolza surface
In Riemann surfaceRiemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
theory, the Bolza surface
Bolza surface
In mathematics, the Bolza surface, alternatively, complex algebraic Bolza curve , is a compact Riemann surface of genus 2 with the highest possible order of the conformal automorphism group in this genus, namely 48. An affine model for the Bolza surface can be obtained as the locus of the...
, sometimes called the Bolza curve, is obtained as the ramified double cover of the Riemann sphere, with ramification locus at the set of vertices of the regular inscribed octahedron. Its automorphism group includes the hyperelliptic involution which flips the two sheets of the cover. The quotient by the order 2 subgroup generated by the hyperelliptic involution yields precisely the group of symmetries of the octahedron. Among the many remarkable properties of the Bolza surface is the fact that it maximizes the systole among all genus 2 hyperbolic surfaces.
Chiral solids with octahedral rotational symmetry
 |
 |
- Note to Pentagonal icositetrahedron: (Ccw) - note that, not very clear in the image, at some vertices 4 faces meet (in the edge of the image)
Archimedean solids
| Name | picture | Faces | Edges | Vertices | Vertex configuration | |
|---|---|---|---|---|---|---|
| snub cube Snub cube In geometry, the snub cube, or snub cuboctahedron, is an Archimedean solid.The snub cube has 38 faces, 6 of which are squares and the other 32 are equilateral triangles. It has 60 edges and 24 vertices. It is a chiral polyhedron, that is, it has two distinct forms, which are mirror images of each... or snub cuboctahedron (2 chiral forms) |
  |
38 | 32 triangles 6 squares |
60 | 24 | 3,3,3,3,4 |
Catalan solids
| Name | picture | Dual Archimedean solid | Faces | Edges | Vertices | Face Polygon |
|---|---|---|---|---|---|---|
| pentagonal icositetrahedron Pentagonal icositetrahedron In geometry, a pentagonal icositetrahedron is a Catalan solid which is the dual of the snub cube. It has two distinct forms, which are mirror images of each other.... |
  (Video)(Video) |
snub cube Snub cube In geometry, the snub cube, or snub cuboctahedron, is an Archimedean solid.The snub cube has 38 faces, 6 of which are squares and the other 32 are equilateral triangles. It has 60 edges and 24 vertices. It is a chiral polyhedron, that is, it has two distinct forms, which are mirror images of each... |
24 | 60 | 38 | irregular pentagon Pentagon In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and... |
Platonic solids
| Name | Picture | Faces | Edges | Vertices | Edges per face | Faces meeting at each vertex |
|---|---|---|---|---|---|---|
| cube (hexahedron) |  (Animation) |
6 | 12 | 8 | 4 | 3 |
| octahedron Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
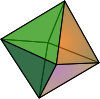 |
8 | 12 | 6 | 3 | 4 |
Archimedean solids
(semi-regular: vertex-uniform)| Name | picture | Faces | Edges | Vertices | Vertex configuration | |
|---|---|---|---|---|---|---|
| cuboctahedron Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... (quasi-regular: vertex- and edge-uniform) |
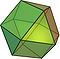 |
14 | 8 triangles 6 square Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles... s |
24 | 12 | 3,4,3,4 |
| truncated cube Truncated cube In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices.... or truncated hexahedron |
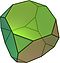 |
14 | 8 triangles 6 octagons |
36 | 24 | 3,8,8 |
| truncated octahedron Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron.... |
 |
14 | 6 squares 8 hexagons |
36 | 24 | 4,6,6 |
| rhombicuboctahedron Rhombicuboctahedron In geometry, the rhombicuboctahedron, or small rhombicuboctahedron, is an Archimedean solid with eight triangular and eighteen square faces. There are 24 identical vertices, with one triangle and three squares meeting at each. Note that six of the squares only share vertices with the triangles... or small rhombicuboctahedron |
 |
26 | 8 triangles 18 squares |
48 | 24 | 3,4,4,4 |
| truncated cuboctahedron Truncated cuboctahedron In geometry, the truncated cuboctahedron is an Archimedean solid. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices and 72 edges... or great rhombicuboctahedron |
 |
26 | 12 squares 8 hexagons 6 octagons |
72 | 48 | 4,6,8 |
Catalan solids
(semi-regular duals: face-uniform)| Name | picture | Dual Archimedean solid | Faces | Edges | Vertices | Face polygon |
|---|---|---|---|---|---|---|
| rhombic dodecahedron Rhombic dodecahedron In geometry, the rhombic dodecahedron is a convex polyhedron with 12 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. Its dual is the cuboctahedron.-Properties:... (quasi-regular dual: face- and edge-uniform) |
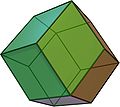 (Video) |
cuboctahedron Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... |
12 | 24 | 14 | rhombus Rhombus In Euclidean geometry, a rhombus or rhomb is a convex quadrilateral whose four sides all have the same length. The rhombus is often called a diamond, after the diamonds suit in playing cards, or a lozenge, though the latter sometimes refers specifically to a rhombus with a 45° angle.Every... |
| triakis octahedron Triakis octahedron In geometry, a triakis octahedron is an Archimedean dual solid, or a Catalan solid. Its dual is the truncated cube.It can be seen as an octahedron with triangular pyramids added to each face; that is, it is the Kleetope of the octahedron. It is also sometimes called a trisoctahedron, or, more... |
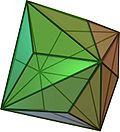 (Video) |
truncated cube Truncated cube In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices.... |
24 | 36 | 14 | isosceles triangle |
| tetrakis hexahedron Tetrakis hexahedron In geometry, a tetrakis hexahedron is a Catalan solid. Its dual is the truncated octahedron, an Archimedean solid. It can be seen as a cube with square pyramids covering each square face; that is, it is the Kleetope of the cube.... |
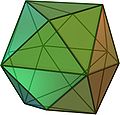 (Video) |
truncated octahedron Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron.... |
24 | 36 | 14 | isosceles triangle |
| deltoidal icositetrahedron Deltoidal icositetrahedron In geometry, a deltoidal icositetrahedron is a Catalan solid which looks a bit like an overinflated cube. Its dual polyhedron is the rhombicuboctahedron.... |
 (Video) |
rhombicuboctahedron Rhombicuboctahedron In geometry, the rhombicuboctahedron, or small rhombicuboctahedron, is an Archimedean solid with eight triangular and eighteen square faces. There are 24 identical vertices, with one triangle and three squares meeting at each. Note that six of the squares only share vertices with the triangles... |
24 | 48 | 26 | kite Kite (geometry) In Euclidean geometry a kite is a quadrilateral whose four sides can be grouped into two pairs of equal-length sides that are next to each other. In contrast, a parallelogram also has two pairs of equal-length sides, but they are opposite each other rather than next to each other... |
| disdyakis dodecahedron Disdyakis dodecahedron In geometry, a disdyakis dodecahedron, or hexakis octahedron, is a Catalan solid and the dual to the Archimedean truncated cuboctahedron. As such it is face-transitive but with irregular face polygons... or hexakis octahedron |
 (Video) |
truncated cuboctahedron Truncated cuboctahedron In geometry, the truncated cuboctahedron is an Archimedean solid. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices and 72 edges... |
48 | 72 | 26 | scalene triangle |
See also
- tetrahedral symmetryTetrahedral symmetry150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
- icosahedral symmetryIcosahedral symmetryA regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...
- binary octahedral group
- hyperoctahedral groupHyperoctahedral groupIn mathematics, a hyperoctahedral group is an important type of group that can be realized as the group of symmetries of a hypercube or of a cross-polytope. Groups of this type are identified by a parameter n, the dimension of the hypercube....

