Dihedral symmetry in three dimensions
Encyclopedia
This article deals with three infinite sequences of point groups in three dimensions
which have a symmetry group
that as abstract group is a dihedral group
Dihn ( n ≥ 2 ).
See also point groups in two dimensions
.
Chiral:
Achiral:
For a given n, all three have n-fold rotational symmetry
about one axis (rotation
by an angle of 360°/n does not change the object), and 2-fold about a perpendicular axis, hence about n of those. For n = ∞ they correspond to three frieze group
s. Schönflies notation
is used, and, in parentheses, Orbifold notation. The term horizontal (h) is used with respect to a vertical axis of rotation.
In 2D the symmetry group Dn includes reflections in lines. When the 2D plane is embedded horizontally in a 3D space, such a reflection can either be viewed as the restriction to that plane of a reflection in a vertical plane, or as the restriction to the plane of a rotation about the reflection line, by 180°. In 3D the two operations are distinguished: the group Dn contains rotations only, not reflections. The other group is pyramidal symmetry Cnv of the same order.
With reflection symmetry
with respect to a plane perpendicular to the n-fold rotation axis we have Dnh (*22n).
Dnd (or Dnv) has vertical mirror planes between the horizontal rotation axes, not through them. As a result the vertical axis is a 2n-fold rotoreflection axis.
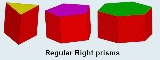
Dnh is the symmetry group for a regular n-sided prisms
and also for a regular n-sided bipyramid
. Dnd is the symmetry group for a regular n-sided antiprism
, and also for a regular n-sided trapezohedron
. Dn is the symmetry group of a partially rotated prism.
n = 1 is not included because the three symmetries are equal to other ones:
For n = 2 there is not one main axes and two additional axes, but there are three equivalent ones.
For Dnd
Dnd is also subgroup of D2nh.
See also cyclic symmetries
D5h (*225):
D4d (2*4):
D5d (2*5):
D17d (*22(17)):
Point groups in three dimensions
In geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O, the group of all isometries that leave the origin fixed, or correspondingly, the group...
which have a symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
that as abstract group is a dihedral group
Dihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
Dihn ( n ≥ 2 ).
See also point groups in two dimensions
Point groups in two dimensions
In geometry, a two-dimensional point group or rosette group is a group of geometric symmetries that keep at least one point fixed in a plane. Every such group is a subgroup of the orthogonal group O, including O itself...
.
Chiral:
- Dn (22n) of order 2n – dihedral symmetry (abstract group DnDihedral groupIn mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
)
Achiral:
- Dnh (*22n) of order 4n – prismatic symmetry (abstract group Dn × C2)
- Dnd (or Dnv) (2*n) of order 4n – antiprismatic symmetry (abstract group D2n)
For a given n, all three have n-fold rotational symmetry
Rotational symmetry
Generally speaking, an object with rotational symmetry is an object that looks the same after a certain amount of rotation. An object may have more than one rotational symmetry; for instance, if reflections or turning it over are not counted, the triskelion appearing on the Isle of Man's flag has...
about one axis (rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
by an angle of 360°/n does not change the object), and 2-fold about a perpendicular axis, hence about n of those. For n = ∞ they correspond to three frieze group
Frieze group
A frieze group is a mathematical concept to classify designs on two-dimensional surfaces which are repetitive in one direction, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art...
s. Schönflies notation
Schoenflies notation
The Schoenflies notation or Schönflies notation, named after the German mathematician Arthur Moritz Schoenflies, is one of two conventions commonly used to describe Point groups. This notation is used in spectroscopy. The other convention is the Hermann–Mauguin notation, also known as the...
is used, and, in parentheses, Orbifold notation. The term horizontal (h) is used with respect to a vertical axis of rotation.
In 2D the symmetry group Dn includes reflections in lines. When the 2D plane is embedded horizontally in a 3D space, such a reflection can either be viewed as the restriction to that plane of a reflection in a vertical plane, or as the restriction to the plane of a rotation about the reflection line, by 180°. In 3D the two operations are distinguished: the group Dn contains rotations only, not reflections. The other group is pyramidal symmetry Cnv of the same order.
With reflection symmetry
Reflection symmetry
Reflection symmetry, reflectional symmetry, line symmetry, mirror symmetry, mirror-image symmetry, or bilateral symmetry is symmetry with respect to reflection. That is, a figure which does not change upon undergoing a reflection has reflectional symmetry.In 2D there is a line of symmetry, in 3D a...
with respect to a plane perpendicular to the n-fold rotation axis we have Dnh (*22n).
Dnd (or Dnv) has vertical mirror planes between the horizontal rotation axes, not through them. As a result the vertical axis is a 2n-fold rotoreflection axis.
Dnh is the symmetry group for a regular n-sided prisms
Prism (geometry)
In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
and also for a regular n-sided bipyramid
Bipyramid
An n-gonal bipyramid or dipyramid is a polyhedron formed by joining an n-gonal pyramid and its mirror image base-to-base.The referenced n-gon in the name of the bipyramids is not an external face but an internal one, existing on the primary symmetry plane which connects the two pyramid halves.The...
. Dnd is the symmetry group for a regular n-sided antiprism
Antiprism
In geometry, an n-sided antiprism is a polyhedron composed of two parallel copies of some particular n-sided polygon, connected by an alternating band of triangles...
, and also for a regular n-sided trapezohedron
Trapezohedron
The n-gonal trapezohedron, antidipyramid or deltohedron is the dual polyhedron of an n-gonal antiprism. Its 2n faces are congruent kites . The faces are symmetrically staggered.The n-gon part of the name does not reference the faces here but arrangement of vertices around an axis of symmetry...
. Dn is the symmetry group of a partially rotated prism.
n = 1 is not included because the three symmetries are equal to other ones:
- D1 and C2: group of order 2 with a single 180° rotation
- D1h and C2v: group of order 4 with a reflection in a plane and a 180° rotation through a line in that plane
- D1d and C2h: group of order 4 with a reflection in a plane and a 180° rotation through a line perpendicular to that plane
For n = 2 there is not one main axes and two additional axes, but there are three equivalent ones.
- D2 (222) of order 4 is one of the three symmetry group types with the Klein four-groupKlein four-groupIn mathematics, the Klein four-group is the group Z2 × Z2, the direct product of two copies of the cyclic group of order 2...
as abstract group. It has three perpendicular 2-fold rotation axes. It is the symmetry group of a cuboidCuboidIn geometry, a cuboid is a solid figure bounded by six faces, forming a convex polyhedron. There are two competing definitions of a cuboid in mathematical literature...
with an S written on two opposite faces, in the same orientation. - D2h (*222) of order 8 is the symmetry group of a cuboid
- D2d (2*2) of order 8 is the symmetry group of e.g.:
- a square cuboid with a diagonal drawn on one square face, and a perpendicular diagonal on the other one
- a regular tetrahedronTetrahedronIn geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
scaled in the direction of a line connecting the midpoints of two opposite edges (D2d is a subgroup of TdTetrahedral symmetry150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
, by scaling we reduce the symmetry).
Subgroups
For Dnh- Cnh
- Cnv
- Dn
For Dnd
- S2n
- Cnv
- Dn
Dnd is also subgroup of D2nh.
See also cyclic symmetries
Cyclic symmetries
This article deals with the four infinite series of point groups in three dimensions with n-fold rotational symmetry about one axis , and no other rotational symmetry :Chiral:*Cn of order n - n-fold rotational symmetry...
Examples
Dnh (*22n): 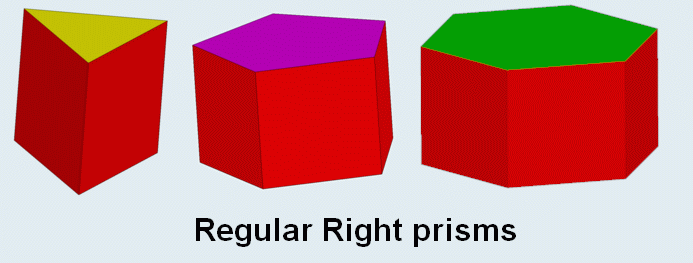 prisms Prism (geometry) In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a... |
D5h (*225):
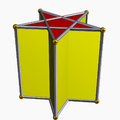 Pentagrammic prism Pentagrammic prism In geometry, the pentagrammic prism is one in an infinite set of nonconvex prisms formed by square sides and two regular star polygon caps, in this case two pentagrams.This polyhedron is identified with the indexed name U78 as a uniform polyhedron.... |
 Pentagrammic antiprism Pentagrammic antiprism In geometry, the pentagrammic antiprism is one in an infinite set of nonconvex antiprisms formed by triangle sides and two regular star polygon caps, in this case two pentagrams.This polyhedron is identified with the indexed name U79 as a uniform polyhedron.... |
D4d (2*4):
 Snub square antiprism Snub square antiprism In geometry, the snub square antiprism is one of theJohnson solids .It is one of the elementary Johnson solids that do not arise from "cut and paste" manipulations of the Platonic and Archimedean solids, although it is a relative of the Icosahedron that has fourfold symmetry instead of... |
D5d (2*5):
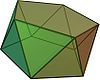 Pentagonal antiprism Pentagonal antiprism In geometry, the pentagonal antiprism is the third in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps. It consists of two pentagons joined to each other by a ring of 10 triangles for a total of 12 faces... |
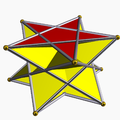 Pentagrammic crossed-antiprism Pentagrammic crossed-antiprism In geometry, the pentagrammic crossed-antiprism is one in an infinite set of nonconvex antiprisms formed by triangle sides and two regular star polygon caps, in this case two pentagrams.... |
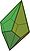 pentagonal trapezohedron Pentagonal trapezohedron The pentagonal trapezohedron or deltohedron is the third in an infinite series of face-transitive polyhedra which are dual polyhedra to the antiprisms. It has ten faces which are congruent kites.... |
D17d (*22(17)):
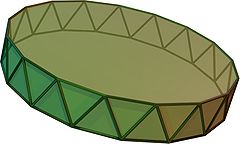 Heptadecagonal antiprism Antiprism In geometry, an n-sided antiprism is a polyhedron composed of two parallel copies of some particular n-sided polygon, connected by an alternating band of triangles... |
See also
- List of spherical symmetry groups
- Point groups in three dimensionsPoint groups in three dimensionsIn geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O, the group of all isometries that leave the origin fixed, or correspondingly, the group...
- Cyclic symmetriesCyclic symmetriesThis article deals with the four infinite series of point groups in three dimensions with n-fold rotational symmetry about one axis , and no other rotational symmetry :Chiral:*Cn of order n - n-fold rotational symmetry...

