In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, a prismatoid is a polyhedron

Polyhedron

In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...

 where all vertices lie in two parallel planes. (If both planes have the same number of vertices

Vertex (geometry)

In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...

,
and the lateral faces are either parallelograms or trapezoids, it is called a prismoid.)

If the areas of the two parallel faces are A₁ and A₃, the cross-sectional area of the intersection of the prismatoid with a plane midway between the two parallel faces is A₂, and the height (the distance between the two parallel faces) is h, then the volume of the prismatoid is given by 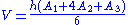(This formula follows immediately by integrating the area parallel to the two planes of vertices by Simpson's rule

Simpson's rule

In numerical analysis, Simpson's rule is a method for numerical integration, the numerical approximation of definite integrals. Specifically, it is the following approximation:...

, since that rule is exact for integration of polynomials of degree up to 3, and in this case the area is at most a quadratic in the height.)







Families of prismatoids include:

• Pyramids
  Pyramid (geometry)
  In geometry, a pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex. Each base edge and apex form a triangle. It is a conic solid with polygonal base....
  
  , where one plane contains only a single point;
• Wedges
  Wedge (geometry)
  In solid geometry, a wedge is a polyhedron defined by two triangles and three trapezoid faces. A wedge has five faces, nine edges, and six vertices.A wedge is a subclass of the prismatoids with the base and opposite ridge in two parallel planes....
  
  , where one plane contains only two points;
• Prisms
  Prism (geometry)
  In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
  
  , where the polygons in each plane are congruent and joined by rectangles or parallelograms;
• Antiprism
  Antiprism
  In geometry, an n-sided antiprism is a polyhedron composed of two parallel copies of some particular n-sided polygon, connected by an alternating band of triangles...
  
  s, where the polygons in each plane are congruent and joined by an alternating strip of triangles;
• Crossed antiprisms;
• Cupolas
  Cupola (geometry)
  In geometry, a cupola is a solid formed by joining two polygons, one with twice as many edges as the other, by an alternating band of triangles and rectangles...
  
  , where the polygon in one plane contains twice as many points as the other and is joined to it by alternating triangles and rectangles;
• Frusta
  Frustum
  In geometry, a frustum is the portion of a solid that lies between two parallel planes cutting it....
  
   obtained by truncation
  Truncation (geometry)
  In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :...
  
   of a pyramid;
• Quadrilateral
  Quadrilateral
  In Euclidean plane geometry, a quadrilateral is a polygon with four sides and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon , hexagon and so on...
  
  -faced hexahedral
  Hexahedron
  A hexahedron is any polyhedron with six faces, although usually implies the cube as a regular hexahedron with all its faces square, and three squares around each vertex....
  
   prismatoids:
  1. Parallelepiped
     Parallelepiped
     In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms. By analogy, it relates to a parallelogram just as a cube relates to a square. In Euclidean geometry, its definition encompasses all four concepts...
     
     s - six parallelogram
     Parallelogram
     In Euclidean geometry, a parallelogram is a convex quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure...
     
      faces
  2. Rhombohedron
     Rhombohedron
     In geometry, a rhombohedron is a three-dimensional figure like a cube, except that its faces are not squares but rhombi. It is a special case of a parallelepiped where all edges are the same length....
     
     s - six rhombus
     Rhombus
     In Euclidean geometry, a rhombus or rhomb is a convex quadrilateral whose four sides all have the same length. The rhombus is often called a diamond, after the diamonds suit in playing cards, or a lozenge, though the latter sometimes refers specifically to a rhombus with a 45° angle.Every...
     
      faces
  3. Trigonal trapezohedra
     Trigonal trapezohedron
     In geometry, the trigonal trapezohedron or deltohedron is the first in an infinite series of face-uniform polyhedra which are dual to the antiprisms. It has six faces which are congruent rhombi....
     
      - six congruent rhombus faces
  4. Cuboid
     Cuboid
     In geometry, a cuboid is a solid figure bounded by six faces, forming a convex polyhedron. There are two competing definitions of a cuboid in mathematical literature...
     
     s - six rectangular faces
  5. Quadrilateral frusta
     Frustum
     In geometry, a frustum is the portion of a solid that lies between two parallel planes cutting it....
     
      - an apex
     Apex (geometry)
     In geometry, an apex is the vertex which is in some sense the highest of the figure to which it belongs.*In an isosceles triangle, the apex is the vertex where the two sides of equal length meet, opposite the unequal third side....
     
     -truncated
     Truncation (geometry)
     In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :...
     
      square pyramid
     Square pyramid
     In geometry, a square pyramid is a pyramid having a square base. If the apex is perpendicularly above the center of the square, it will have C4v symmetry.- Johnson solid :...
     
     
  6. Cube
     Cube
     In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
     
     s - six square faces

In general a polytope

Polytope

In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...

 is prismatioidal if its vertices exist in two hyperplane

Hyperplane

A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...

s.