
Per Enflo
Encyclopedia
Per H. Enflo (ˌpæːɹ ˈeːnfluː; born 1944) is a mathematician who has solved fundamental problems in functional analysis
. Three of these problems had been open
for more than forty years:
In solving these problems, Enflo developed new techniques which were then used by other researchers in functional analysis
and operator theory
for years. Some of Enflo's research has been important also in other mathematical fields, such as number theory
, and in computer science
, especially computer algebra and approximation algorithm
s.
Enflo works at Kent State University
, where he holds the title of University Professor. Enflo has earlier held positions at the University of California, Berkeley
, Stanford University
, École Polytechnique
, (Paris
) and The Royal Institute of Technology
, Stockholm
.
Enflo is also a concert pianist.
, Functional analysis
is concerned with the study of vector space
s and operators acting upon them. It has its historical roots in the study of functional spaces, in particular transformations of functions
, such as the Fourier transform
, as well as in the study of differential and integral equations. In functional analysis, an important class of vector spaces consists of the complete
normed vector space
s over the real
or complex
numbers, which are called Banach space
s. An important example of a Banach space is a Hilbert space
, where the norm
arises from an inner product
. Hilbert spaces are of fundamental importance in many areas, including the mathematical formulation of quantum mechanics
, stochastic processes, and time-series analysis. Besides studying spaces of functions, functional analysis also studies the continuous linear operators
on spaces of functions.
in the spirit of functional analysis. In two years, 1969–1970, Enflo published five papers on Hilbert's fifth problem; these papers are collected in Enflo (1970), along with a short summary. Some of the results of the these papers are described in Enflo (1976) and in the last chapter of Benyamini and Lindenstrauss
.
. Algorithm theorists
derive approximation algorithm
s that embed finite metric-spaces into low-dimensional Euclidean space
s with low "distortion" (in Gromov's terminology for the Lipschitz
category
; c.f. Banach–Mazur distance). Low-dimensional problems have lower computational complexity
, of course. More importantly, if the problems embed well in either the Euclidean plane or the three-dimensional Euclidean space
, then geometric algorithm
s become exceptionally fast.
However, such embedding
techniques have limitations, as shown by Enflo's (1969) theorem:
This theorem, "found by Enflo [1969], is probably the first result showing an unbounded distortion for embedding
s into Euclidean space
s. Enflo considered the problem of uniform
embeddability among Banach space
s, and the distortion was an auxiliary device in his proof."
so that, for every there is some
there is some  so that for any two vectors with
so that for any two vectors with  and
and 

implies that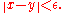
Intuitively, the center of a line segment inside the unit ball must lie deep inside the unit ball unless the segment is short.
In 1972 Enflo proved that "every super-reflexive
Banach space
admits an equivalent uniformly convex
norm".
, the "Goose problem
" of Stanislaw Mazur
, and the approximation problem of Alexander Grothendieck
. Grothendieck had shown that his approximation problem was the central problem in the theory
of Banach space
s and continuous linear operator
s.
have a Schauder basis
.
A Schauder basis or countable basis is similar to the usual (Hamel) basis
of a vector space
; the difference is that for Hamel bases we use linear combination
s that are finite sums, while for Schauder bases they may be infinite sums. This makes Schauder bases more suitable for the analysis of infinite-dimensional topological vector space
s including Banach space
s.
Schauder bases were described by Juliusz Schauder
in 1927. Let V denote a Banach space
over the field
F. A Schauder basis is a sequence
(bn) of elements of V such that for every element v ∈ V there exists a unique sequence (αn) of elements in F so that
where the convergence
is understood with respect to the norm
topology
. Schauder bases can also be defined analogously in a general topological vector space
.

. When a problem was especially interesting and when its solution seemed difficult, the problem would be written down in the book of problems, which soon became known as the Scottish Book
. For problems that seemed especially important or difficult or both, the problem's proposer would often pledge to award a prize for its solution.
On 6 November 1936, Stanislaw Mazur
posed a problem on representing continuous functions. Formally writing down problem 153 in the Scottish Book, Mazur promised as the reward a "live goose", an especially rich price during the Great Depression
and on the eve of World War II
.
Fairly soon afterwords, it was realized that Mazur's problem was closely related to Banach's problem on the existence of Schauder bases in separable Banach spaces. Most of the other problems in the Scottish Book were solved regularly. However, there was little progress on Mazur's problem and a few other problems, which became famous open problem
s to mathematicians around the world.
of Banach spaces and continuous linear operator
s introduced the approximation property
. A Banach space
is said to have the approximation property
, if every compact operator
is a limit of finite-rank operators. The converse is always true.
In a long monograph, Grothendieck proved that if every Banach space had the approximation property, then every Banach space would have a Schauder basis. Grothendieck thus focused the attention of functional analysts on deciding whether every Banach space have the approximation property.
in Warsaw; the "goose reward" ceremony was broadcast throughout Poland
.
In functional analysis
, one of the most prominent problems was the invariant subspace problem, which required the evaluation of the truth of the following proposition:
For Banach space
s, the first example of an operator without an invariant subspace was constructed by Enflo. (For Hilbert space
s, the invariant subspace problem remains open
.)
Enflo proposed a solution to the invariant subspace problem in 1975, publishing an outline in 1976. Enflo submitted the full article in 1981 and the article's complexity and length delayed its publication to 1987 Enflo's long "manuscript had a world-wide circulation among mathematicians" and some of its ideas were described in publications besides Enflo (1976). Enflo's works inspired a similar construction of an operator without an invariant subspace for example by Beauzamy, who acknowledged Enflo's ideas.
In the 1990s, Enflo developed a "constructive" approach to the invariant subspace problem on Hilbert spaces.
 and
and  , there exists
, there exists 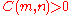 such that for all homogeneous polynomial
such that for all homogeneous polynomial
s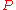 and
and  of degrees
of degrees  and
and  (in
(in 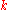 variables), then
variables), then
where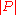 denotes the sum of the absolute values of the coefficients of
denotes the sum of the absolute values of the coefficients of 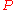 . Enflo proved that
. Enflo proved that  does not depend on the number of variables
does not depend on the number of variables 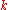 . Enflo's original proof was simplified by Montgomery.
. Enflo's original proof was simplified by Montgomery.
This result was generalized to other norm
s on the vector space of homogeneous polynomial
s. Of these norms, the most used has been the Bombieri norm
.
The Bombieri norm
is defined in terms of the following scalar product:
For all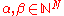 we have
we have
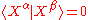 if
if 
where we use use the following notation:
if , we write
, we write 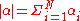 and
and
 and
and 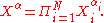
The most remarkable property of this norm is the Bombieri inequality:
Let be two homogeneous polynomial
be two homogeneous polynomial
s respectively of degree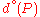 and
and 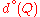 with
with  variables, then, the following inequality holds:
variables, then, the following inequality holds:
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
. Three of these problems had been open
Open problem
In science and mathematics, an open problem or an open question is a known problem that can be accurately stated, and has not yet been solved . Some questions remain unanswered for centuries before solutions are found...
for more than forty years:
- The basis problem and the approximation problemApproximation propertyIn mathematics, a Banach space is said to have the approximation property , if every compact operator is a limit of finite-rank operators. The converse is always true....
and later - the invariant subspace problem for Banach spaces.
In solving these problems, Enflo developed new techniques which were then used by other researchers in functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
and operator theory
Operator theory
In mathematics, operator theory is the branch of functional analysis that focuses on bounded linear operators, but which includes closed operators and nonlinear operators.Operator theory also includes the study of algebras of operators....
for years. Some of Enflo's research has been important also in other mathematical fields, such as number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, and in computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, especially computer algebra and approximation algorithm
Approximation algorithm
In computer science and operations research, approximation algorithms are algorithms used to find approximate solutions to optimization problems. Approximation algorithms are often associated with NP-hard problems; since it is unlikely that there can ever be efficient polynomial time exact...
s.
Enflo works at Kent State University
Kent State University
Kent State University is a public research university located in Kent, Ohio, United States. The university has eight campuses around the northeast Ohio region with the main campus in Kent being the largest...
, where he holds the title of University Professor. Enflo has earlier held positions at the University of California, Berkeley
University of California, Berkeley
The University of California, Berkeley , is a teaching and research university established in 1868 and located in Berkeley, California, USA...
, Stanford University
Stanford University
The Leland Stanford Junior University, commonly referred to as Stanford University or Stanford, is a private research university on an campus located near Palo Alto, California. It is situated in the northwestern Santa Clara Valley on the San Francisco Peninsula, approximately northwest of San...
, École Polytechnique
École Polytechnique
The École Polytechnique is a state-run institution of higher education and research in Palaiseau, Essonne, France, near Paris. Polytechnique is renowned for its four year undergraduate/graduate Master's program...
, (Paris
Paris
Paris is the capital and largest city in France, situated on the river Seine, in northern France, at the heart of the Île-de-France region...
) and The Royal Institute of Technology
Royal Institute of Technology
The Royal Institute of Technology is a university in Stockholm, Sweden. KTH was founded in 1827 as Sweden's first polytechnic and is one of Scandinavia's largest institutions of higher education in technology. KTH accounts for one-third of Sweden’s technical research and engineering education...
, Stockholm
Stockholm
Stockholm is the capital and the largest city of Sweden and constitutes the most populated urban area in Scandinavia. Stockholm is the most populous city in Sweden, with a population of 851,155 in the municipality , 1.37 million in the urban area , and around 2.1 million in the metropolitan area...
.
Enflo is also a concert pianist.
Enflo's contributions to functional analysis and operator theory
In mathematicsMathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, Functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
is concerned with the study of vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s and operators acting upon them. It has its historical roots in the study of functional spaces, in particular transformations of functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
, such as the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
, as well as in the study of differential and integral equations. In functional analysis, an important class of vector spaces consists of the complete
Complete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
normed vector space
Normed vector space
In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
s over the real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
or complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
numbers, which are called Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s. An important example of a Banach space is a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
, where the norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
arises from an inner product
Inner product space
In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
. Hilbert spaces are of fundamental importance in many areas, including the mathematical formulation of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, stochastic processes, and time-series analysis. Besides studying spaces of functions, functional analysis also studies the continuous linear operators
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
on spaces of functions.
Hilbert's fifth problem and embeddings
At Stockholm University, Hans Rådström suggested that Enflo consider Hilbert's fifth problemHilbert's fifth problem
Hilbert's fifth problem, is the fifth mathematical problem from the problem-list publicized in 1900 by mathematician David Hilbert, and concerns the characterization of Lie groups. The theory of Lie groups describes continuous symmetry in mathematics; its importance there and in theoretical physics...
in the spirit of functional analysis. In two years, 1969–1970, Enflo published five papers on Hilbert's fifth problem; these papers are collected in Enflo (1970), along with a short summary. Some of the results of the these papers are described in Enflo (1976) and in the last chapter of Benyamini and Lindenstrauss
Joram Lindenstrauss
Joram Lindenstrauss is an Israeli mathematician working in functional analysis. He is professor emeritus of mathematics at the Einstein Institute of Mathematics, Hebrew University of Jerusalem, Israel.-Biography:...
.
Applications in computer science
Enflo's techniques have found application in computer scienceComputer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
. Algorithm theorists
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
derive approximation algorithm
Approximation algorithm
In computer science and operations research, approximation algorithms are algorithms used to find approximate solutions to optimization problems. Approximation algorithms are often associated with NP-hard problems; since it is unlikely that there can ever be efficient polynomial time exact...
s that embed finite metric-spaces into low-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
s with low "distortion" (in Gromov's terminology for the Lipschitz
Lipschitz continuity
In mathematical analysis, Lipschitz continuity, named after Rudolf Lipschitz, is a strong form of uniform continuity for functions. Intuitively, a Lipschitz continuous function is limited in how fast it can change: for every pair of points on the graph of this function, the absolute value of the...
category
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
; c.f. Banach–Mazur distance). Low-dimensional problems have lower computational complexity
Computational Complexity
Computational Complexity may refer to:*Computational complexity theory*Computational Complexity...
, of course. More importantly, if the problems embed well in either the Euclidean plane or the three-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, then geometric algorithm
Computational geometry
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational...
s become exceptionally fast.
However, such embedding
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
techniques have limitations, as shown by Enflo's (1969) theorem:
- For every
 , the Hamming cube
, the Hamming cube  cannot be embedded with "distortion
cannot be embedded with "distortion  " (or less) into
" (or less) into  -dimensional Euclidean space if
-dimensional Euclidean space if  . Consequently, the optimal embedding is the natural embedding, which realizes
. Consequently, the optimal embedding is the natural embedding, which realizes 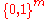 as a subspace of
as a subspace of  -dimensional Euclidean space.
-dimensional Euclidean space.
This theorem, "found by Enflo [1969], is probably the first result showing an unbounded distortion for embedding
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
s into Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
s. Enflo considered the problem of uniform
Uniform continuity
In mathematics, a function f is uniformly continuous if, roughly speaking, it is possible to guarantee that f and f be as close to each other as we please by requiring only that x and y are sufficiently close to each other; unlike ordinary continuity, the maximum distance between x and y cannot...
embeddability among Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s, and the distortion was an auxiliary device in his proof."
Geometry of Banach spaces
A uniformly convex space is a Banach spaceBanach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
so that, for every
 there is some
there is some  so that for any two vectors with
so that for any two vectors with  and
and 

implies that
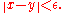
Intuitively, the center of a line segment inside the unit ball must lie deep inside the unit ball unless the segment is short.
In 1972 Enflo proved that "every super-reflexive
Reflexive space
In functional analysis, a Banach space is called reflexive if it coincides with the dual of its dual space in the topological and algebraic senses. Reflexive Banach spaces are often characterized by their geometric properties.- Normed spaces :Suppose X is a normed vector space over R or C...
Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
admits an equivalent uniformly convex
Uniformly convex space
In mathematics, uniformly convex spaces are common examples of reflexive Banach spaces. The concept of uniform convexity was first introduced by James A...
norm".
The basis problem and Mazur's goose
With one paper, which was published in 1973, Per Enflo solved three problems that had stumped functional analysts for decades: The basis problem of Stefan BanachStefan Banach
Stefan Banach was a Polish mathematician who worked in interwar Poland and in Soviet Ukraine. He is generally considered to have been one of the 20th century's most important and influential mathematicians....
, the "Goose problem
Scottish Book
The Scottish Book was a thick notebook used by mathematicians of the Lwow School of Mathematics for jotting down problems meant to be solved. The notebook was named after the "Scottish Café" where it was kept....
" of Stanislaw Mazur
Stanislaw Mazur
Stanisław Mazur was a Polish mathematician and a member of the Polish Academy of Sciences....
, and the approximation problem of Alexander Grothendieck
Alexander Grothendieck
Alexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
. Grothendieck had shown that his approximation problem was the central problem in the theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
of Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s and continuous linear operator
Continuous linear operator
In functional analysis and related areas of mathematics, a continuous linear operator or continuous linear mapping is a continuous linear transformation between topological vector spaces....
s.
Basis problem of Banach
The basis problem was posed by Stefan Banach in his book, Theory of Linear Operators. Banach asked whether every Banach spaceBanach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
have a Schauder basis
Schauder basis
In mathematics, a Schauder basis or countable basis is similar to the usual basis of a vector space; the difference is that Hamel bases use linear combinations that are finite sums, while for Schauder bases they may be infinite sums...
.
A Schauder basis or countable basis is similar to the usual (Hamel) basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
of a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
; the difference is that for Hamel bases we use linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
s that are finite sums, while for Schauder bases they may be infinite sums. This makes Schauder bases more suitable for the analysis of infinite-dimensional topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
s including Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s.
Schauder bases were described by Juliusz Schauder
Juliusz Schauder
Juliusz Paweł Schauder was a Polish mathematician of Jewish origin, known for his work in functional analysis, partial differential equation and mathematical physics.Born on September 21, 1899 in Lemberg, he had to fight in World War I right after his graduation from school...
in 1927. Let V denote a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
over the field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F. A Schauder basis is a sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
(bn) of elements of V such that for every element v ∈ V there exists a unique sequence (αn) of elements in F so that

where the convergence
Convergence
-Mathematics:* Convergence , refers to the notion that some functions and sequences approach a limit under certain conditions* Convergence , the notion that a sequence of transformations come to the same conclusion, no matter what order they are performed in.-Natural sciences:*Convergence ,...
is understood with respect to the norm
Norm
-In academia:A designated standard of average performance of people of a given age, background, etc.*Norm , a set of statements used to regulate artificial intelligence software...
topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
. Schauder bases can also be defined analogously in a general topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
.

Problem 153 in the Scottish Book: Mazur's goose
Banach and other Polish mathematicians would work on mathematical problems at the Scottish CaféScottish Café
The Scottish Café was the café in Lwów where, in the 1930s and 1940s, mathematicians from the Lwów School collaboratively discussed research problems, particularly in functional analysis and topology....
. When a problem was especially interesting and when its solution seemed difficult, the problem would be written down in the book of problems, which soon became known as the Scottish Book
Scottish Book
The Scottish Book was a thick notebook used by mathematicians of the Lwow School of Mathematics for jotting down problems meant to be solved. The notebook was named after the "Scottish Café" where it was kept....
. For problems that seemed especially important or difficult or both, the problem's proposer would often pledge to award a prize for its solution.
On 6 November 1936, Stanislaw Mazur
Stanislaw Mazur
Stanisław Mazur was a Polish mathematician and a member of the Polish Academy of Sciences....
posed a problem on representing continuous functions. Formally writing down problem 153 in the Scottish Book, Mazur promised as the reward a "live goose", an especially rich price during the Great Depression
Great Depression
The Great Depression was a severe worldwide economic depression in the decade preceding World War II. The timing of the Great Depression varied across nations, but in most countries it started in about 1929 and lasted until the late 1930s or early 1940s...
and on the eve of World War II
World War II
World War II, or the Second World War , was a global conflict lasting from 1939 to 1945, involving most of the world's nations—including all of the great powers—eventually forming two opposing military alliances: the Allies and the Axis...
.
Fairly soon afterwords, it was realized that Mazur's problem was closely related to Banach's problem on the existence of Schauder bases in separable Banach spaces. Most of the other problems in the Scottish Book were solved regularly. However, there was little progress on Mazur's problem and a few other problems, which became famous open problem
Open problem
In science and mathematics, an open problem or an open question is a known problem that can be accurately stated, and has not yet been solved . Some questions remain unanswered for centuries before solutions are found...
s to mathematicians around the world.
Grothendieck's formulation of the approximation problem
Grothendieck's work on the theoryCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
of Banach spaces and continuous linear operator
Continuous linear operator
In functional analysis and related areas of mathematics, a continuous linear operator or continuous linear mapping is a continuous linear transformation between topological vector spaces....
s introduced the approximation property
Approximation property
In mathematics, a Banach space is said to have the approximation property , if every compact operator is a limit of finite-rank operators. The converse is always true....
. A Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
is said to have the approximation property
Approximation property
In mathematics, a Banach space is said to have the approximation property , if every compact operator is a limit of finite-rank operators. The converse is always true....
, if every compact operator
Compact operator
In functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y...
is a limit of finite-rank operators. The converse is always true.
In a long monograph, Grothendieck proved that if every Banach space had the approximation property, then every Banach space would have a Schauder basis. Grothendieck thus focused the attention of functional analysts on deciding whether every Banach space have the approximation property.
Enflo's solution
In 1972, Per Enflo constructed a separable Banach space that lacks the approximation property and a Schauder basis. In 1972, Mazur awarded a live goose to Enflo in a ceremony at the Stefan Banach CenterStefan Banach
Stefan Banach was a Polish mathematician who worked in interwar Poland and in Soviet Ukraine. He is generally considered to have been one of the 20th century's most important and influential mathematicians....
in Warsaw; the "goose reward" ceremony was broadcast throughout Poland
Poland
Poland , officially the Republic of Poland , is a country in Central Europe bordered by Germany to the west; the Czech Republic and Slovakia to the south; Ukraine, Belarus and Lithuania to the east; and the Baltic Sea and Kaliningrad Oblast, a Russian exclave, to the north...
.
Invariant subspace problem and polynomials
In functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, one of the most prominent problems was the invariant subspace problem, which required the evaluation of the truth of the following proposition:
- Given a complex Banach spaceBanach spaceIn mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
H of dimensionDimension (vector space)In mathematics, the dimension of a vector space V is the cardinality of a basis of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension...
> 1 and a bounded linear operatorBounded operatorIn functional analysis, a branch of mathematics, a bounded linear operator is a linear transformation L between normed vector spaces X and Y for which the ratio of the norm of L to that of v is bounded by the same number, over all non-zero vectors v in X...
T : H → H, then H has a non-trivial closedClosed setIn geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
T-invariant subspaceInvariant subspaceIn mathematics, an invariant subspace of a linear mappingfrom some vector space V to itself is a subspace W of V such that T is contained in W...
, i.e. there exists a closed linear subspaceLinear subspaceThe concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
W of H which is different from {0} and H such that T(W) ⊆ W.
For Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s, the first example of an operator without an invariant subspace was constructed by Enflo. (For Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s, the invariant subspace problem remains open
Unsolved problems in mathematics
This article lists some unsolved problems in mathematics. See individual articles for details and sources.- Millennium Prize Problems :Of the seven Millennium Prize Problems set by the Clay Mathematics Institute, six have yet to be solved:* P versus NP...
.)
Enflo proposed a solution to the invariant subspace problem in 1975, publishing an outline in 1976. Enflo submitted the full article in 1981 and the article's complexity and length delayed its publication to 1987 Enflo's long "manuscript had a world-wide circulation among mathematicians" and some of its ideas were described in publications besides Enflo (1976). Enflo's works inspired a similar construction of an operator without an invariant subspace for example by Beauzamy, who acknowledged Enflo's ideas.
In the 1990s, Enflo developed a "constructive" approach to the invariant subspace problem on Hilbert spaces.
Multiplicative inequalities for homogeneous polynomials
An essential idea in Enflo's construction was "concentration of polynomials at low degrees": For all positive integers and
and  , there exists
, there exists 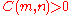 such that for all homogeneous polynomial
such that for all homogeneous polynomialHomogeneous polynomial
In mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
s
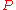 and
and  of degrees
of degrees  and
and  (in
(in 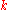 variables), then
variables), thenwhere
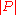 denotes the sum of the absolute values of the coefficients of
denotes the sum of the absolute values of the coefficients of 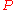 . Enflo proved that
. Enflo proved that  does not depend on the number of variables
does not depend on the number of variables 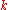 . Enflo's original proof was simplified by Montgomery.
. Enflo's original proof was simplified by Montgomery.This result was generalized to other norm
Normed vector space
In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
s on the vector space of homogeneous polynomial
Homogeneous polynomial
In mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
s. Of these norms, the most used has been the Bombieri norm
Bombieri norm
In mathematics, the Bombieri norm, named after Enrico Bombieri, is a norm on homogeneous polynomials with coefficient in \mathbb R or \mathbb C...
.
Bombieri norm
The Bombieri norm
Bombieri norm
In mathematics, the Bombieri norm, named after Enrico Bombieri, is a norm on homogeneous polynomials with coefficient in \mathbb R or \mathbb C...
is defined in terms of the following scalar product:
For all
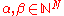 we have
we have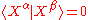 if
if 
- For every
 we define
we define 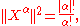
where we use use the following notation:
if
 , we write
, we write 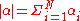 and
and and
and 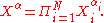
The most remarkable property of this norm is the Bombieri inequality:
Let
 be two homogeneous polynomial
be two homogeneous polynomialHomogeneous polynomial
In mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
s respectively of degree
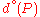 and
and 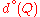 with
with  variables, then, the following inequality holds:
variables, then, the following inequality holds:-
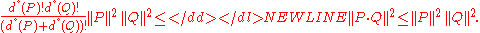
In the above statement, the Bombieri inequality is the left-hand side inequality; the right-hand side inequality means that the Bombieri normBombieri normIn mathematics, the Bombieri norm, named after Enrico Bombieri, is a norm on homogeneous polynomials with coefficient in \mathbb R or \mathbb C...
is a norm of the algebra of polynomials under multiplication.
The Bombieri inequality implies that the product of two polynomials cannot be arbitrarily small, and this lower-bound is fundamental in applications like polynomial factorizationPolynomial factorizationIn mathematics and computer algebra, polynomial factorization refers to factoring a polynomial into irreducible polynomials over a given field.-Formulation of the question:...
(or in Enflo's construction of an operator without an invariant subspace).
Applications
Enflo's idea of "concentration of polynomials at low degrees" has led to important publications in number theoryNumber theoryNumber theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
algebraicAlgebraic geometryAlgebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
and Diophantine geometryDiophantine geometryIn mathematics, diophantine geometry is one approach to the theory of Diophantine equations, formulating questions about such equations in terms of algebraic geometry over a ground field K that is not algebraically closed, such as the field of rational numbers or a finite field, or more general...
, and polynomial factorizationPolynomial factorizationIn mathematics and computer algebra, polynomial factorization refers to factoring a polynomial into irreducible polynomials over a given field.-Formulation of the question:...
.
Mathematical biology: Population dynamics
In applied mathematicsApplied mathematicsApplied mathematics is a branch of mathematics that concerns itself with mathematical methods that are typically used in science, engineering, business, and industry. Thus, "applied mathematics" is a mathematical science with specialized knowledge...
, Per Enflo has published several papers in mathematical biologyMathematical biologyMathematical and theoretical biology is an interdisciplinary scientific research field with a range of applications in biology, medicine and biotechnology...
, specifically in population dynamicsPopulation dynamicsPopulation dynamics is the branch of life sciences that studies short-term and long-term changes in the size and age composition of populations, and the biological and environmental processes influencing those changes...
.
Human evolution
Enflo has also published in population geneticsPopulation geneticsPopulation genetics is the study of allele frequency distribution and change under the influence of the four main evolutionary processes: natural selection, genetic drift, mutation and gene flow. It also takes into account the factors of recombination, population subdivision and population...
and paleoanthropologyPaleoanthropologyPaleoanthropology, which combines the disciplines of paleontology and physical anthropology, is the study of ancient humans as found in fossil hominid evidence such as petrifacted bones and footprints.-19th century:...
.
Today, all humans belong to one, undivided by species barrier, population of Homo sapiens sapiens. However, according to the "Out of Africa" model this is not the first species of hominids: the first species of genus Homo, Homo habilis, evolved in East Africa at least 2 Ma, and members of this species populated different parts of Africa in a relatively short time. Homo erectus evolved more than 1.8 Ma, and by 1.5 Ma had spread throughout the Old WorldOld WorldThe Old World consists of those parts of the world known to classical antiquity and the European Middle Ages. It is used in the context of, and contrast with, the "New World" ....
.
Anthropologists have been divided as to whether current human population evolved as one interconnected population (as postulated by the Multiregional Evolution hypothesis), or evolved only in East Africa, speciatedSpeciationSpeciation is the evolutionary process by which new biological species arise. The biologist Orator F. Cook seems to have been the first to coin the term 'speciation' for the splitting of lineages or 'cladogenesis,' as opposed to 'anagenesis' or 'phyletic evolution' occurring within lineages...
, and then migrating out of Africa and replaced human populations in EurasiaEurasiaEurasia is a continent or supercontinent comprising the traditional continents of Europe and Asia ; covering about 52,990,000 km2 or about 10.6% of the Earth's surface located primarily in the eastern and northern hemispheres...
(called the "Out of Africa" Model or the "Complete Replacement" Model).
Neanderthals and modern humans coexisted in Europe for several thousand years, but the duration of this period is uncertain. Modern humans may have first migrated to Europe 40–43,000 years ago. Neanderthals may have lived as recently as 24,000 years ago in refugia on the south coast of the Iberian peninsula such as Gorham's CaveGorham's CaveGorham's Cave is a natural sea cave in Gibraltar, considered to be one of the last known habitations of the Neanderthals. It is located on the south east face of the Rock of Gibraltar...
. Inter-stratification of Neanderthal and modern human remains has been suggested, but is disputed.
With HawksJohn D. HawksJohn Hawks is a professor of Anthropology at the University of Wisconsin–Madison. He also is the author of a widely read paleoanthropology blog.-Biography:...
and WolpoffMilford H. WolpoffMilford H. Wolpoff is a paleoanthropologist, and since 1977, a professor of anthropology and adjunct associate research scientist, Museum of Anthropology at the University of Michigan...
, Enflo published an explanation of fossil evidence on the DNADNADeoxyribonucleic acid is a nucleic acid that contains the genetic instructions used in the development and functioning of all known living organisms . The DNA segments that carry this genetic information are called genes, but other DNA sequences have structural purposes, or are involved in...
of NeanderthalNeanderthalThe Neanderthal is an extinct member of the Homo genus known from Pleistocene specimens found in Europe and parts of western and central Asia...
and modern humans. This article tries to resolve a debate in the evolution of modern humans between theories suggesting either multiregionalMultiregional origin of modern humansThe multiregional hypothesis is a scientific model that provides an explanation for the pattern of human evolution. The hypothesis holds that humans first arose near the beginning of the Pleistocene two million years ago and subsequent human evolution has been within a single, continuous human...
and single AfricanRecent African origin of modern humansIn paleoanthropology, the recent African origin of modern humans is the most widely accepted model describing the origin and early dispersal of anatomically modern humans...
origins. In particular,
the extinction of NeanderthalsNeanderthal extinction hypothesesNeanderthal extinction hypotheses are theories about how Neanderthals became extinct around 30,000 years ago. Since their discovery, both the Neanderthals' place in the human family tree and their relation to modern Europeans has been hotly debated...
could have happened due to waves of modern humans entered Europe – in technical terms, due to "the continuous influx of modern human DNA into the Neandertal gene pool."
Enflo has also written about the population dynamics of zebra mussels in Lake ErieLake ErieLake Erie is the fourth largest lake of the five Great Lakes in North America, and the tenth largest globally. It is the southernmost, shallowest, and smallest by volume of the Great Lakes and therefore also has the shortest average water residence time. It is bounded on the north by the...
.

Piano
Per Enflo is also a concert pianist.
A child prodigyChild prodigyA child prodigy is someone who, at an early age, masters one or more skills far beyond his or her level of maturity. One criterion for classifying prodigies is: a prodigy is a child, typically younger than 18 years old, who is performing at the level of a highly trained adult in a very demanding...
in both music and mathematics, Enflo won the Swedish competition for young pianists at age 11 in 1956, and he won the same competition in 1961. At age 12, Enflo appeared as a soloist with the Royal Opera Orchestra of Sweden. He debuted in the Stockholm Concert HallStockholm Concert HallThe Stockholm Concert Hall is the main hall for orchestral music in Stockholm, Sweden. Designed by Ivar Tengbom and inaugurated in 1926, it is the home to the Royal Stockholm Philharmonic Orchestra. It is also where the awarding ceremony for the Nobel Prizes, Polar Music Prize are held annually....
in 1963. Enflo's teachers included Bruno Seidlhofer, Géza AndaGéza AndaGéza Anda was a Hungarian pianist. A celebrated interpreter of classical and romantic repertoire, particularly noted for his performances and recordings of Mozart, he was also a tremendous interpreter of Beethoven, Schumann, Brahms and Bartók....
, and Gottfried Boon (who himself was a student of Arthur Schnabel).
In 1999 Enflo competed in the first annual Van Cliburn FoundationVan Cliburn FoundationThe Van Cliburn Foundation is host to the Van Cliburn International Piano Competition, the International Piano Competition for Outstanding Amateurs™, Musical Awakenings® education programs, and Cliburn Concerts.-Mission:...
’s International Piano CompetitionVan Cliburn International Piano CompetitionThe Van Cliburn International Piano Competition was first held in 1962 in Fort Worth, Texas and is hosted by Van Cliburn Foundation. It was created by Fort Worth area teachers in honor of Van Cliburn, who had won the first International Tchaikovsky Competition four years prior with Tchaikovsky's...
for Outstanding Amateurs.
Enflo performs regularly around KentKent, OhioKent is a city in the U.S. state of Ohio and the largest city in Portage County. It is located along the Cuyahoga River in Northeastern Ohio on the western edge of the county. The population was 27,906 at the 2000 United States Census and 28,904 in the 2010 Census...
and in a Mozart series in Columbus, OhioColumbus, OhioColumbus is the capital of and the largest city in the U.S. state of Ohio. The broader metropolitan area encompasses several counties and is the third largest in Ohio behind those of Cleveland and Cincinnati. Columbus is the third largest city in the American Midwest, and the fifteenth largest city...
(with the Triune Festival Orchestra). His solo piano recitals have appeared on the Classics Network of the radio station WOSUWOSU-FMWOSU-FM — branded 89.7fm NPR News — is a National Public Radio news and talk radio station licensed to Columbus, Ohio and serving the Columbus metro area. It is owned by Ohio State University. The station has multiple repeaters throughout the U.S...
, which is sponsored by Ohio State UniversityOhio State UniversityThe Ohio State University, commonly referred to as Ohio State, is a public research university located in Columbus, Ohio. It was originally founded in 1870 as a land-grant university and is currently the third largest university campus in the United States...
.
See also
- Approximation problem
- Approximation propertyApproximation propertyIn mathematics, a Banach space is said to have the approximation property , if every compact operator is a limit of finite-rank operators. The converse is always true....
- Banach spaceBanach spaceIn mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
- Bombieri normBombieri normIn mathematics, the Bombieri norm, named after Enrico Bombieri, is a norm on homogeneous polynomials with coefficient in \mathbb R or \mathbb C...
- Compact operatorCompact operatorIn functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y...
- Hilbert's fifth problemHilbert's fifth problemHilbert's fifth problem, is the fifth mathematical problem from the problem-list publicized in 1900 by mathematician David Hilbert, and concerns the characterization of Lie groups. The theory of Lie groups describes continuous symmetry in mathematics; its importance there and in theoretical physics...
(infinite-dimensional)
- Invariant subspace problem
- renorms
- superreflexiveReflexive spaceIn functional analysis, a Banach space is called reflexive if it coincides with the dual of its dual space in the topological and algebraic senses. Reflexive Banach spaces are often characterized by their geometric properties.- Normed spaces :Suppose X is a normed vector space over R or C...
- Schauder basisSchauder basisIn mathematics, a Schauder basis or countable basis is similar to the usual basis of a vector space; the difference is that Hamel bases use linear combinations that are finite sums, while for Schauder bases they may be infinite sums...
- Scottish BookScottish BookThe Scottish Book was a thick notebook used by mathematicians of the Lwow School of Mathematics for jotting down problems meant to be solved. The notebook was named after the "Scottish Café" where it was kept....
(MazurStanislaw MazurStanisław Mazur was a Polish mathematician and a member of the Polish Academy of Sciences....
's problem) - uniformly convex spaceUniformly convex spaceIn mathematics, uniformly convex spaces are common examples of reflexive Banach spaces. The concept of uniform convexity was first introduced by James A...
External sources
- Biography of Per Enflo at Canisius CollegeCanisius CollegeCanisius College is a private Roman Catholic college in Buffalo, New York, United States. The college was founded in 1870 by members of the Society of Jesus from Germany and is named after St. Peter Canisius. The college is one of 28 institutions in the Association of Jesuit Colleges and...
- Homepage of Per Enflo at Kent State University
Databases


