Schauder basis
Encyclopedia
In mathematics
, a Schauder basis or countable basis is similar to the usual (Hamel) basis
of a vector space
; the difference is that Hamel bases use linear combination
s that are finite sums, while for Schauder bases they may be infinite sums. This makes Schauder bases more suitable for the analysis of infinite-dimensional topological vector space
s including Banach space
s.
Schauder bases were described by Juliusz Schauder
in 1927, although such bases were discussed earlier. For example, the Haar basis was given in 1909, and discussed a basis for continuous functions on an interval, sometimes called a Faber–Schauder system.
over the field
F. A Schauder basis is a sequence
(bn) of elements of V such that for every element v ∈ V there exists a unique sequence (αn) of elements in F so that
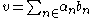
where the convergence is understood with respect to the norm topology. Schauder bases can also be defined analogously in a general topological vector space
.
As opposed to a Hamel basis, the elements of the basis must be ordered since the series may not converge unconditionally.
and lp
for 1 ≤ p < ∞ are Schauder bases.
Every orthonormal basis
in a separable Hilbert space
is a Schauder basis.
The Haar system
is an example of a basis for Lp(0, 1)
with 1 ≤ p < ∞. Another example is the trigonometric system defined below.
The Banach space C([0, 1]) of continuous functions on the interval [0, 1], with the supremum norm, admits a Schauder basis.
A Banach space with a Schauder basis is necessarily separable, but the converse is false, as described below. Every Banach space with a Schauder basis has the approximation property
.
who constructed a separable Banach space without a Schauder basis.
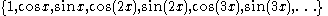
or (in the complex case)
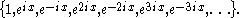
The sequence (xn) (called the trigonometric system) is a Schauder basis for the space Lp[0, 2π
] for any p > 1. For p = 2, this is the content of the Riesz–Fischer theorem
. However, the set (xn) is not a Schauder basis for L1[0, 2π]. This means that there are functions in L1 whose Fourier series does not converge in the L1 norm.
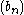is unconditional if whenever the series 
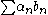converges, it converges
unconditionally. Unconditionality is an important property since it allows us to forget about the order of summation.
The standard bases of the sequence space
s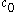
and 
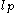for 1 ≤ p < ∞, as well as every orthonormal basis in a Hilbert space, are unconditional.
The trigonometric system is not an unconditional basis in Lp, except for p = 2.
The Haar system is a unconditional basis in Lp for any 1 < p < ∞. Actually, the space L1 has no unconditional basis.
A natural question is whether every infinite-dimensional Banach space has a infinite-dimensional subspace with an unconditional basis. This was solved negatively by Timothy Gowers and Bernard Maurey in 1992.
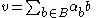
with αb ∈ F, with the extra condition that the set
is finite. This property makes the Hamel basis unwieldy for infinite-dimensional Banach spaces; as a Hamel basis for an infinite-dimensional Banach space would be uncountable. (Every finite dimensional subspace of an infinite-dimensional Banach space X has empty interior, and is no-where dense in X. It then follows from the Baire category theorem
that the a countable union of these finite-dimensional subspaces cannot serve as a basis.)
A family of vectors is total if its linear span
(the set of finite linear combinations) is dense in V. Every complete set of vectors is total, but the converse need not hold in an infinite-dimensional space.
If V is an inner product space
, an orthogonal basis
is a subset B such that its linear span is dense in V and elements in the basis are pairwise orthogonal.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Schauder basis or countable basis is similar to the usual (Hamel) basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
of a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
; the difference is that Hamel bases use linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
s that are finite sums, while for Schauder bases they may be infinite sums. This makes Schauder bases more suitable for the analysis of infinite-dimensional topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
s including Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s.
Schauder bases were described by Juliusz Schauder
Juliusz Schauder
Juliusz Paweł Schauder was a Polish mathematician of Jewish origin, known for his work in functional analysis, partial differential equation and mathematical physics.Born on September 21, 1899 in Lemberg, he had to fight in World War I right after his graduation from school...
in 1927, although such bases were discussed earlier. For example, the Haar basis was given in 1909, and discussed a basis for continuous functions on an interval, sometimes called a Faber–Schauder system.
Definition
Let V denote a Banach spaceBanach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
over the field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F. A Schauder basis is a sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
(bn) of elements of V such that for every element v ∈ V there exists a unique sequence (αn) of elements in F so that
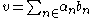
where the convergence is understood with respect to the norm topology. Schauder bases can also be defined analogously in a general topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
.
As opposed to a Hamel basis, the elements of the basis must be ordered since the series may not converge unconditionally.
Examples and properties
The standard bases of c0Sequence space
In functional analysis and related areas of mathematics, a sequence space is a vector space whose elements are infinite sequences of real or complex numbers. Equivalently, it is a function space whose elements are functions from the natural numbers to the field K of real or complex numbers...
and lp
Sequence space
In functional analysis and related areas of mathematics, a sequence space is a vector space whose elements are infinite sequences of real or complex numbers. Equivalently, it is a function space whose elements are functions from the natural numbers to the field K of real or complex numbers...
for 1 ≤ p < ∞ are Schauder bases.
Every orthonormal basis
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
in a separable Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
is a Schauder basis.
The Haar system
Haar wavelet
In mathematics, the Haar wavelet is a certain sequence of rescaled "square-shaped" functions which together form a wavelet family or basis. Wavelet analysis is similar to Fourier analysis in that it allows a target function over an interval to be represented in terms of an orthonormal function basis...
is an example of a basis for Lp(0, 1)
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
with 1 ≤ p < ∞. Another example is the trigonometric system defined below.
The Banach space C([0, 1]) of continuous functions on the interval [0, 1], with the supremum norm, admits a Schauder basis.
A Banach space with a Schauder basis is necessarily separable, but the converse is false, as described below. Every Banach space with a Schauder basis has the approximation property
Approximation property
In mathematics, a Banach space is said to have the approximation property , if every compact operator is a limit of finite-rank operators. The converse is always true....
.
Basis problem
A theorem of Mazur asserts that every infinite-dimensional Banach space has an infinite-dimensional subspace that has a Schauder basis. A question of Banach asked whether every separable Banach space has a Schauder basis; this was negatively answered by Per EnfloPer Enflo
Per H. Enflo is a mathematician who has solved fundamental problems in functional analysis. Three of these problems had been open for more than forty years:* The basis problem and the approximation problem and later...
who constructed a separable Banach space without a Schauder basis.
Relation to Fourier series
Let (xn) be the sequence (in the real case)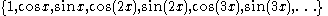or (in the complex case)
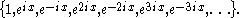
The sequence (xn) (called the trigonometric system) is a Schauder basis for the space Lp[0, 2π
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
] for any p > 1. For p = 2, this is the content of the Riesz–Fischer theorem
Riesz–Fischer theorem
In mathematics, the Riesz–Fischer theorem in real analysis refers to a number of closely related results concerning the properties of the space L2 of square integrable functions...
. However, the set (xn) is not a Schauder basis for L1[0, 2π]. This means that there are functions in L1 whose Fourier series does not converge in the L1 norm.
Unconditionality
A Schauder basis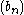 is unconditional if whenever the series 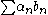converges, it convergesunconditionally. Unconditionality is an important property since it allows us to forget about the order of summation.
The standard bases of the sequence space
Sequence space
In functional analysis and related areas of mathematics, a sequence space is a vector space whose elements are infinite sequences of real or complex numbers. Equivalently, it is a function space whose elements are functions from the natural numbers to the field K of real or complex numbers...
s
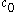and 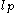for 1 ≤ p < ∞, as well as every orthonormal basis in a Hilbert space, are unconditional.The trigonometric system is not an unconditional basis in Lp, except for p = 2.
The Haar system is a unconditional basis in Lp for any 1 < p < ∞. Actually, the space L1 has no unconditional basis.
A natural question is whether every infinite-dimensional Banach space has a infinite-dimensional subspace with an unconditional basis. This was solved negatively by Timothy Gowers and Bernard Maurey in 1992.
Related concepts
A Hamel basis is a subset B of a vector space V such that every element v ∈ V can uniquely be written as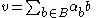with αb ∈ F, with the extra condition that the set
is finite. This property makes the Hamel basis unwieldy for infinite-dimensional Banach spaces; as a Hamel basis for an infinite-dimensional Banach space would be uncountable. (Every finite dimensional subspace of an infinite-dimensional Banach space X has empty interior, and is no-where dense in X. It then follows from the Baire category theorem
Baire category theorem
The Baire category theorem is an important tool in general topology and functional analysis. The theorem has two forms, each of which gives sufficient conditions for a topological space to be a Baire space....
that the a countable union of these finite-dimensional subspaces cannot serve as a basis.)
A family of vectors is total if its linear span
Linear span
In the mathematical subfield of linear algebra, the linear span of a set of vectors in a vector space is the intersection of all subspaces containing that set...
(the set of finite linear combinations) is dense in V. Every complete set of vectors is total, but the converse need not hold in an infinite-dimensional space.
If V is an inner product space
Inner product space
In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
, an orthogonal basis
Orthogonal basis
In mathematics, particularly linear algebra, an orthogonal basis for an inner product space is a basis for whose vectors are mutually orthogonal...
is a subset B such that its linear span is dense in V and elements in the basis are pairwise orthogonal.