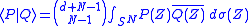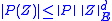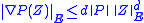Bombieri norm
Encyclopedia
In mathematics
, the Bombieri norm, named after Enrico Bombieri
, is a norm
on homogeneous polynomial
s with coefficient in or
or  (there is also a version for non homogeneous univariate polynomials). This norm has many remarkable properties, the most important being listed in this article.
(there is also a version for non homogeneous univariate polynomials). This norm has many remarkable properties, the most important being listed in this article.
s with N variables can be defined as follows using multi-index notation
:
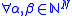
by definition different monomials are orthogonal, so that
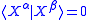 if
if 
while
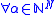
by definition
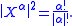
In the above definition and in the rest of this article the following notation applies:
if
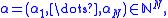
write
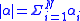
and
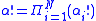
and
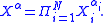
let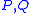 be two homogeneous polynomials respectively of degree
be two homogeneous polynomials respectively of degree 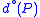 and
and 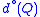 with
with  variables, then, the following inequality holds:
variables, then, the following inequality holds:
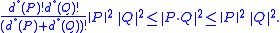
Here the Bombieri inequality is the left hand side of the above statement, while the right side means that the Bombieri norm is an algebra norm. Giving the left hand side is meaningless withot that constraint, because in this case, we can achieve the same result with any norm by multiplying the norm by a well chosen factor.
This multiplicative inequality implies that the product of two polynomials is bounded from below by a quantity that depends on the multiplicand polynomials. Thus, this product can not be arbitrarily small. This multiplicative inequality is useful in metric algebraic geometry
and number theory
.
isometry
:
let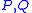 be two homogeneous polynomials of degree
be two homogeneous polynomials of degree  with
with  variables and let
variables and let 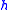 be an isometry
be an isometry
of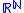 (or
(or 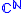 ). Then, the we have
). Then, the we have 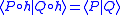 . When
. When  this implies
this implies 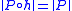 .
.
This result follows from a nice integral formulation of the scalar product:
where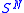 is the unit sphere of
is the unit sphere of 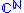 with its canonical measure
with its canonical measure 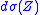 .
.
 be a homogeneous polynomial of degree
be a homogeneous polynomial of degree  with
with  variables and let
variables and let 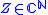 . We have:
. We have:
where denotes the Euclidean norm.
denotes the Euclidean norm.
The Bombieri norm is useful in polynomial factorization, where it has some advantages over the Mahler measure, according to Knuth (Exercises 20-21, pages 457-458 and 682-684).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Bombieri norm, named after Enrico Bombieri
Enrico Bombieri
Enrico Bombieri is a mathematician who has been working at the Institute for Advanced Study in Princeton, New Jersey. Bombieri's research in number theory, algebraic geometry, and mathematical analysis have earned him many international prizes --- a Fields Medal in 1974 and the Balzan Prize in 1980...
, is a norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
on homogeneous polynomial
Homogeneous polynomial
In mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
s with coefficient in
 or
or  (there is also a version for non homogeneous univariate polynomials). This norm has many remarkable properties, the most important being listed in this article.
(there is also a version for non homogeneous univariate polynomials). This norm has many remarkable properties, the most important being listed in this article.Bombieri scalar product for homogeneous polynomials
To start with the geometry, the Bombieri scalar product for homogeneous polynomialHomogeneous polynomial
In mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
s with N variables can be defined as follows using multi-index notation
Multi-index notation
The mathematical notation of multi-indices simplifies formulae used in multivariable calculus, partial differential equations and the theory of distributions, by generalising the concept of an integer index to an ordered tuple of indices....
:
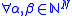
by definition different monomials are orthogonal, so that
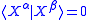 if
if 
while
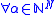
by definition
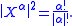
In the above definition and in the rest of this article the following notation applies:
if
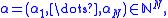
write
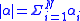
and
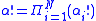
and
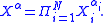
Bombieri inequality
The fundamental property of this norm is the Bombieri inequality:let
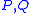 be two homogeneous polynomials respectively of degree
be two homogeneous polynomials respectively of degree 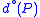 and
and 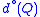 with
with  variables, then, the following inequality holds:
variables, then, the following inequality holds: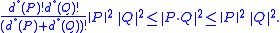
Here the Bombieri inequality is the left hand side of the above statement, while the right side means that the Bombieri norm is an algebra norm. Giving the left hand side is meaningless withot that constraint, because in this case, we can achieve the same result with any norm by multiplying the norm by a well chosen factor.
This multiplicative inequality implies that the product of two polynomials is bounded from below by a quantity that depends on the multiplicand polynomials. Thus, this product can not be arbitrarily small. This multiplicative inequality is useful in metric algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
and number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
.
Invariance by isometry
Another important property is that the Bombieri norm is invariant by composition with anisometry
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
:
let
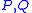 be two homogeneous polynomials of degree
be two homogeneous polynomials of degree  with
with  variables and let
variables and let 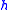 be an isometry
be an isometryof
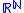 (or
(or 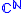 ). Then, the we have
). Then, the we have 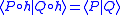 . When
. When  this implies
this implies 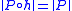 .
.This result follows from a nice integral formulation of the scalar product:
where
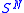 is the unit sphere of
is the unit sphere of 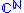 with its canonical measure
with its canonical measure 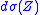 .
.Other inequalities
Let be a homogeneous polynomial of degree
be a homogeneous polynomial of degree  with
with  variables and let
variables and let 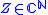 . We have:
. We have:where
 denotes the Euclidean norm.
denotes the Euclidean norm.The Bombieri norm is useful in polynomial factorization, where it has some advantages over the Mahler measure, according to Knuth (Exercises 20-21, pages 457-458 and 682-684).
See also
- Grassmann manifold
- Hardy spaceHardy spaceIn complex analysis, the Hardy spaces Hp are certain spaces of holomorphic functions on the unit disk or upper half plane. They were introduced by Frigyes Riesz , who named them after G. H. Hardy, because of the paper...
- Homogeneous polynomialHomogeneous polynomialIn mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
- Plücker embeddingPlücker embeddingIn mathematics, the Plücker embedding describes a method to realize the Grassmannian of all r-dimensional subspaces of a vector space V as a subvariety of the projective space of the rth exterior power of that vector space, P....