Antisymmetric relation
Encyclopedia
In mathematics
, a binary relation
R on a set X is antisymmetric if, for all a and b in X
or, equivalently,
In mathematical notation
, this is:
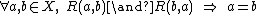
or, equivalently,
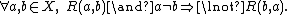
The usual order relation ≤ on the real number
s is antisymmetric: if for two real numbers x and y both inequalities x ≤ y and y ≤ x hold then x and y must be equal. Similarly, given to sets A and B, if every element in A also is in B and every element in B is also in A, then A and B must contain all the same elements and therefore be equal:
Therefore, the subset order ⊆ on the subsets of any given set is antisymmetric.
Partial and total order
s are antisymmetric by definition. A relation can be both symmetric
and antisymmetric (e.g., the equality relation), and there are relations which are neither symmetric nor antisymmetric (e.g., the "preys on" relation on biological species
).
Antisymmetry is different from asymmetry
. According to one definition of asymmetric, anything that fails to be symmetric is asymmetric. Another definition of asymmetric makes asymmetry equivalent to antisymmetry plus irreflexivity
.
s is antisymmetric:
The divisibility order of the natural number
s is another example of an antisymmetric relation.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a binary relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
R on a set X is antisymmetric if, for all a and b in X
- if R(a,b) and R(b,a), then a = b,
or, equivalently,
- if R(a,b) with a ≠ b, then R(b,a) must not hold.
In mathematical notation
Mathematical notation
Mathematical notation is a system of symbolic representations of mathematical objects and ideas. Mathematical notations are used in mathematics, the physical sciences, engineering, and economics...
, this is:
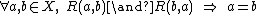
or, equivalently,
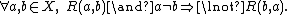
The usual order relation ≤ on the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s is antisymmetric: if for two real numbers x and y both inequalities x ≤ y and y ≤ x hold then x and y must be equal. Similarly, given to sets A and B, if every element in A also is in B and every element in B is also in A, then A and B must contain all the same elements and therefore be equal:

Therefore, the subset order ⊆ on the subsets of any given set is antisymmetric.
Partial and total order
Total order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
s are antisymmetric by definition. A relation can be both symmetric
Symmetric relation
In mathematics, a binary relation R over a set X is symmetric if it holds for all a and b in X that if a is related to b then b is related to a.In mathematical notation, this is:...
and antisymmetric (e.g., the equality relation), and there are relations which are neither symmetric nor antisymmetric (e.g., the "preys on" relation on biological species
Species
In biology, a species is one of the basic units of biological classification and a taxonomic rank. A species is often defined as a group of organisms capable of interbreeding and producing fertile offspring. While in many cases this definition is adequate, more precise or differing measures are...
).
Antisymmetry is different from asymmetry
Asymmetric relation
Asymmetric often means, simply: not symmetric. In this sense an asymmetric relation is a binary relation which is not a symmetric relation.That is,\lnot....
. According to one definition of asymmetric, anything that fails to be symmetric is asymmetric. Another definition of asymmetric makes asymmetry equivalent to antisymmetry plus irreflexivity
Reflexive relation
In mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...
.
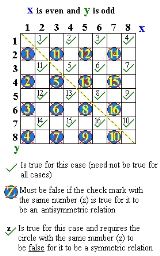
Examples
The relation "x is even, y is odd" between a pair (x, y) of integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s is antisymmetric:
The divisibility order of the natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s is another example of an antisymmetric relation.


