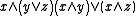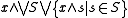Limit-preserving function (order theory)
Encyclopedia
In the mathematical
area of order theory
, one often speaks about function
s that preserve certain limits, i.e. certain suprema
or infima
. Roughly speaking, these functions map the supremum/infimum of a set to the supremum/infimum of the image of the set. Depending on the type of sets for which a function satisfies this property, it may preserve finite, directed, non-empty, or just arbitrary suprema or infima. Each of these requirements appears naturally and frequently in many areas of order theory and there are various important relationships among these concepts and other notions such as monotonicity
. If the implication of limit preservation is inverted, such that the existence of limits in the range of a function implies the existence of limits in the domain, then one obtains functions that are limit-reflecting.
The purpose of this article is to clarify the definition of these basic concepts, which is necessary since the literature is not always consistent at this point, and to give general results and explanations on these issues.
s that are complete
with respect to certain limit constructions. For example, in lattice theory
, one is interested in orders where all finite non-empty sets have both a least upper bound and a greatest lower bound. In domain theory
, on the other hand, one focuses on partially ordered sets in which every directed subset
has a supremum. Complete lattices and orders with a least element (the "empty supremum") provide further examples.
In all these cases, limits play a central role for the theory, which is supported by their interpretations in the practical applications of the various disciplines. Now it is no surprise that one also is interested in specifying appropriate mappings between such orders. From an algebraic
viewpoint, this means that one wants to find adequate notions of homomorphism
s for the structures under consideration. As usually, this is achieved by considering those functions that are compatible with the constructions that are characteristic for the respective orders. For example, lattice homomorphisms are those functions that preserve non-empty finite suprema and infima, i.e. the image of a supremum/infimum of two elements is just the supremum/infimum of their images. In domain theory, one often deals with so-called Scott-continuous functions that preserve all directed suprema.
The background for the definitions and terminology given below is to be found in category theory
, where limits
(and co-limits) in a more general sense are considered. The categorical concept of limit-preserving and limit-reflecting functor
s is in complete harmony with order theory, since orders can be considered as small categories of a certain kind.
Note that this definition consists of two requirements: the supremum of the set f(S) exists and it is equal to f(s). This corresponds to the abovementioned parallel to category theory, but is not always required in the literature. In fact, in some cases one weakens the definition to require only existing suprema to be equal to f(s). However, Wikipedia works with the common notion given above and states the other condition explicitly if required.
From the fundamental definition given above, one can derive a broad range of useful properties. A function f between posets
P and Q is said to preserve finite, non-empty, directed, or arbitrary suprema if it preserves the suprema of all finite, non-empty, directed, or arbitrary sets, respectively. The preservation of non-empty finite suprema can also be defined by the identity f(x v y) = f(x) v f(y), holding for all elements x and y, where we assume v to be a total function on both orders.
In a dual
way, one defines properties for the preservation of infima.
The "opposite" condition to preservation of limits is called reflection. Consider a function f as above and a subset S of P, such that sup f(S) exists in Q and is equal to f(s) for some element s of P. Then f reflects the supremum of S if sup S exists and is equal to s. As already demonstrated for preservation, one obtains many additional properties by considering certain classes of sets S and by dualizing the definition to infima.
s have this property. Conversely, by the order theoretical Adjoint Functor Theorem, mappings that preserve all suprema/infima can be guaranteed to be part of a unique Galois connection as long as some additional requirements are met.
L is distributive if, for all x, y, and z in L, we find
But this just says that the meet function ^: L -> L preserves binary suprema. It is known in lattice theory, that this condition is equivalent to its dual, i.e. the function v: L -> L preserving binary infima. In a similar way, one sees that the infinite distributivity law
of complete Heyting algebra
s (see also pointless topology
) is equivalent to the meet function ^ preserving arbitrary suprema. This condition, however, does not imply its dual.
and topology
. A similar use of the term continuous for preservation of limits can also be found in category theory.
Based on the fact that some limits can be expressed in terms of others, one can derive connections between the preservation properties.
For example, a function f preserves directed suprema if and only if
it preserves the suprema of all ideals.
Furthermore, a mapping f from a poset in which every non-empty finite supremum exists (a so-called sup-semilattice) preserves arbitrary suprema if and only if it preserves both directed and finite (possibly empty) suprema.
However, it is not true that a function that preserves all suprema would also preserve all infima or vice versa.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
area of order theory
Order theory
Order theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
, one often speaks about function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s that preserve certain limits, i.e. certain suprema
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
or infima
Infimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
. Roughly speaking, these functions map the supremum/infimum of a set to the supremum/infimum of the image of the set. Depending on the type of sets for which a function satisfies this property, it may preserve finite, directed, non-empty, or just arbitrary suprema or infima. Each of these requirements appears naturally and frequently in many areas of order theory and there are various important relationships among these concepts and other notions such as monotonicity
Monotonic function
In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
. If the implication of limit preservation is inverted, such that the existence of limits in the range of a function implies the existence of limits in the domain, then one obtains functions that are limit-reflecting.
The purpose of this article is to clarify the definition of these basic concepts, which is necessary since the literature is not always consistent at this point, and to give general results and explanations on these issues.
Background and motivation
In many specialized areas of order theory, one restricts to classes of partially ordered setPartially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
s that are complete
Completeness (order theory)
In the mathematical area of order theory, completeness properties assert the existence of certain infima or suprema of a given partially ordered set . A special use of the term refers to complete partial orders or complete lattices...
with respect to certain limit constructions. For example, in lattice theory
Lattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
, one is interested in orders where all finite non-empty sets have both a least upper bound and a greatest lower bound. In domain theory
Domain theory
Domain theory is a branch of mathematics that studies special kinds of partially ordered sets commonly called domains. Consequently, domain theory can be considered as a branch of order theory. The field has major applications in computer science, where it is used to specify denotational...
, on the other hand, one focuses on partially ordered sets in which every directed subset
Directed set
In mathematics, a directed set is a nonempty set A together with a reflexive and transitive binary relation ≤ , with the additional property that every pair of elements has an upper bound: In other words, for any a and b in A there must exist a c in A with a ≤ c and b ≤...
has a supremum. Complete lattices and orders with a least element (the "empty supremum") provide further examples.
In all these cases, limits play a central role for the theory, which is supported by their interpretations in the practical applications of the various disciplines. Now it is no surprise that one also is interested in specifying appropriate mappings between such orders. From an algebraic
Universal algebra
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
viewpoint, this means that one wants to find adequate notions of homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
s for the structures under consideration. As usually, this is achieved by considering those functions that are compatible with the constructions that are characteristic for the respective orders. For example, lattice homomorphisms are those functions that preserve non-empty finite suprema and infima, i.e. the image of a supremum/infimum of two elements is just the supremum/infimum of their images. In domain theory, one often deals with so-called Scott-continuous functions that preserve all directed suprema.
The background for the definitions and terminology given below is to be found in category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, where limits
Limit (category theory)
In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products and inverse limits....
(and co-limits) in a more general sense are considered. The categorical concept of limit-preserving and limit-reflecting functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
s is in complete harmony with order theory, since orders can be considered as small categories of a certain kind.
Formal definition
Consider two partially ordered sets P and Q, and a function f from P to Q. Furthermore, let S be a subset of P that has a least upper bound s. Then f preserves the supremum of S if the set f(S) = {f(x) | x in S} has a least upper bound in Q which is equal to f(s), i.e.- f(sup S) = sup f(S)
Note that this definition consists of two requirements: the supremum of the set f(S) exists and it is equal to f(s). This corresponds to the abovementioned parallel to category theory, but is not always required in the literature. In fact, in some cases one weakens the definition to require only existing suprema to be equal to f(s). However, Wikipedia works with the common notion given above and states the other condition explicitly if required.
From the fundamental definition given above, one can derive a broad range of useful properties. A function f between posets
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
P and Q is said to preserve finite, non-empty, directed, or arbitrary suprema if it preserves the suprema of all finite, non-empty, directed, or arbitrary sets, respectively. The preservation of non-empty finite suprema can also be defined by the identity f(x v y) = f(x) v f(y), holding for all elements x and y, where we assume v to be a total function on both orders.
In a dual
Duality (order theory)
In the mathematical area of order theory, every partially ordered set P gives rise to a dual partially ordered set which is often denoted by Pop or Pd. This dual order Pop is defined to be the set with the inverse order, i.e. x ≤ y holds in Pop if and only if y ≤ x holds in P...
way, one defines properties for the preservation of infima.
The "opposite" condition to preservation of limits is called reflection. Consider a function f as above and a subset S of P, such that sup f(S) exists in Q and is equal to f(s) for some element s of P. Then f reflects the supremum of S if sup S exists and is equal to s. As already demonstrated for preservation, one obtains many additional properties by considering certain classes of sets S and by dualizing the definition to infima.
Special cases
Some special cases or properties derived from the above scheme are known under other names or are of particular importance to some areas of order theory. For example, functions that preserve the empty supremum are those that preserve the least element. Furthermore, due to the motivation explained earlier, many limit-preserving functions appear as special homomorphisms for certain order structures. Some other prominent cases are given below.Preservation of all limits
An interesting situation occurs if a function preserves all suprema (or infima). More accurately, this is expressed by saying that a function preserves all existing suprema (or infima), and it may well be that the posets under consideration are not complete lattices. For example, (monotone) Galois connectionGalois connection
In mathematics, especially in order theory, a Galois connection is a particular correspondence between two partially ordered sets . The same notion can also be defined on preordered sets or classes; this article presents the common case of posets. Galois connections generalize the correspondence...
s have this property. Conversely, by the order theoretical Adjoint Functor Theorem, mappings that preserve all suprema/infima can be guaranteed to be part of a unique Galois connection as long as some additional requirements are met.
Distributivity
A latticeLattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
L is distributive if, for all x, y, and z in L, we find
But this just says that the meet function ^: L -> L preserves binary suprema. It is known in lattice theory, that this condition is equivalent to its dual, i.e. the function v: L -> L preserving binary infima. In a similar way, one sees that the infinite distributivity law
of complete Heyting algebra
Complete Heyting algebra
In mathematics, especially in order theory, a complete Heyting algebra is a Heyting algebra which is complete as a lattice. Complete Heyting algebras are the objects of three different categories; the category CHey, the category Loc of locales, and its opposite, the category Frm of frames...
s (see also pointless topology
Pointless topology
In mathematics, pointless topology is an approach to topology that avoids mentioning points. The name 'pointless topology' is due to John von Neumann...
) is equivalent to the meet function ^ preserving arbitrary suprema. This condition, however, does not imply its dual.
Scott-continuity
Functions that preserve directed suprema are called Scott-continuous or sometimes just continuous, if this does not cause confusions with the according concept of analysisMathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
and topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
. A similar use of the term continuous for preservation of limits can also be found in category theory.
Important properties and results
The above definition of limit preservation is quite strong. Indeed, every function that preserves at least the suprema or infima of two-element chains, i.e. of sets of two comparable elements, is necessarily monotone. Hence, all the special preservation properties stated above induce monotonicity.Based on the fact that some limits can be expressed in terms of others, one can derive connections between the preservation properties.
For example, a function f preserves directed suprema if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it preserves the suprema of all ideals.
Furthermore, a mapping f from a poset in which every non-empty finite supremum exists (a so-called sup-semilattice) preserves arbitrary suprema if and only if it preserves both directed and finite (possibly empty) suprema.
However, it is not true that a function that preserves all suprema would also preserve all infima or vice versa.