
Nonconvex uniform polyhedron
Encyclopedia

Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a uniform star polyhedron is a self-intersecting uniform polyhedron
Uniform polyhedron
A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
. They are also sometimes called nonconvex polyhedra to imply self-intersecting. Each polyhedron can contain either star polygon faces, star polygon vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
s or both.
The complete set of 57 nonprismatic uniform star polyhedra includes the 4 regular ones, called the Kepler–Poinsot polyhedra, 5 quasiregular ones, and 48 semiregular ones.
There are also two infinite sets of uniform star prisms and uniform star antiprisms.
Just as (nondegenerate) star polygons (which have Polygon density greater than 1) correspond to circular polygons with overlapping tiles, star polyhedra that do not pass through the center have polytope density
Polytope density
In geometry, polytope density represents the number of windings of a polytope, particularly a uniform or regular polytope, around its center. It can be visually determined by counting the minimum number of facet crossings of a ray from the center to infinity...
greater than 1, and correspond to spherical polyhedra with overlapping tiles; there are 48 nonprismatic such uniform star polyhedra. The remaining 9 nonprismatic uniform star polyhedra, those that pass through the center, are the hemipolyhedra, and do not correspond to spherical polyhedra, as the center cannot be projected uniquely onto the sphere.
The nonconvex forms are constructed from Schwarz triangle
Schwarz triangle
In geometry, a Schwarz triangle, named after Hermann Schwarz is a spherical triangle that can be used to tile a sphere, possibly overlapping, through reflections in its edges. They were classified in ....
s.
All the uniform polyhedra are listed below by their symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
s and subgrouped by their vertex arrangements.
Regular polyhedra are labeled by their Schläfli symbol. Other nonregular uniform polyhedra are listed with their vertex configuration
Vertex configuration
In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron...
or their Uniform polyhedron index U(1-80).
Note: For nonconvex forms below an additional descriptor Nonuniform is used when the convex hull
Convex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
vertex arrangement
Vertex arrangement
In geometry, a vertex arrangement is a set of points in space described by their relative positions. They can be described by their use in polytopes....
has same topology as one of these, but has nonregular faces. For example an nonuniform cantellated form may have rectangles created in place of the edges rather than squares
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
.
Tetrahedral symmetry

Tetrahemihexahedron
In geometry, the tetrahemihexahedron or hemicuboctahedron is a uniform star polyhedron, indexed as U4. It has 6 vertices and 12 edges, and 7 faces: 4 triangular and 3 square. Its vertex figure is a crossed quadrilateral. It has Coxeter-Dynkin diagram of ....
and octahemioctahedron
Octahemioctahedron
In geometry, the octahemioctahedron is a nonconvex uniform polyhedron, indexed as U3. Its vertex figure is a crossed quadrilateral.It is one of nine hemipolyhedra with 4 hexagonal faces passing through the model center.- Related polyhedra :...
which have tetrahedral symmetry
Tetrahedral symmetry
150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
(with fundamental domain Mobius triangle (3 3 2)).
There are two Schwarz triangles that generate unique nonconvex uniform polyhedra: one right triangle (3/2 3 2), and one general triangle (3/2 3 3).
| Vertex arrangement Vertex arrangement In geometry, a vertex arrangement is a set of points in space described by their relative positions. They can be described by their use in polytopes.... (Convex hull Convex hull In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X.... ) |
Nonconvex forms |
|---|---|
 Tetrahedron Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
|
 Rectified tetrahedron Octahedron Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
|
 Truncated tetrahedron Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :... |
|
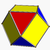 Cantellated tetrahedron (Cuboctahedron Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... ) |
|
 Omnitruncated tetrahedron (Truncated octahedron Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron.... ) |
|
 Snub tetrahedron (Icosahedron Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... ) |
Octahedral symmetry

Octahedral symmetry
150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation...
(with fundamental domain Mobius triangle (4 3 2)).
There are four Schwarz triangles that generate nonconvex forms, two right triangles (3/2 4 2), and (4/3 3 2), and two general triangles: (4/3 4 3), (3/2 4 4).
| Vertex arrangement Vertex arrangement In geometry, a vertex arrangement is a set of points in space described by their relative positions. They can be described by their use in polytopes.... (Convex hull Convex hull In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X.... ) |
Nonconvex forms | ||
|---|---|---|---|
 Cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
|||
 Octahedron Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
|||
 Cuboctahedron Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... |
|||
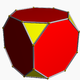 Truncated cube Truncated cube In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices.... |
|||
 Truncated octahedron Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron.... |
|||
 Rhombicuboctahedron Rhombicuboctahedron In geometry, the rhombicuboctahedron, or small rhombicuboctahedron, is an Archimedean solid with eight triangular and eighteen square faces. There are 24 identical vertices, with one triangle and three squares meeting at each. Note that six of the squares only share vertices with the triangles... |
|||
 Nonuniform truncated cuboctahedron Truncated cuboctahedron In geometry, the truncated cuboctahedron is an Archimedean solid. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices and 72 edges... |
|||
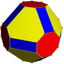 Nonuniform truncated cuboctahedron Truncated cuboctahedron In geometry, the truncated cuboctahedron is an Archimedean solid. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices and 72 edges... |
|||
 Snub cube Snub cube In geometry, the snub cube, or snub cuboctahedron, is an Archimedean solid.The snub cube has 38 faces, 6 of which are squares and the other 32 are equilateral triangles. It has 60 edges and 24 vertices. It is a chiral polyhedron, that is, it has two distinct forms, which are mirror images of each... |
Icosahedral symmetry

Icosahedral symmetry
A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...
(with fundamental domain Mobius triangle (5 3 2)). (or 47 nonconvex forms if Skilling's figure is included). Some of the nonconvex snub forms have reflective vertex symmetry.
| Vertex arrangement Vertex arrangement In geometry, a vertex arrangement is a set of points in space described by their relative positions. They can be described by their use in polytopes.... (Convex hull Convex hull In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X.... ) |
Nonconvex forms | |||||||
|---|---|---|---|---|---|---|---|---|
 {5/2,5} |
 {5,5/2} |
 {3,5/2} |
||||||
 U42 Great ditrigonal dodecicosidodecahedron In geometry, the great ditrigonal dodecicosidodecahedron is a nonconvex uniform polyhedron, indexed as U42.- Related polyhedra :It shares its vertex arrangement with the truncated dodecahedron... |
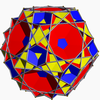 U48 Great icosicosidodecahedron In geometry, the great icosicosidodecahedron is a nonconvex uniform polyhedron, indexed as U48. Its vertex figure is a crossed quadrilateral.- Related polyhedra :It shares its vertex arrangement with the truncated dodecahedron... |
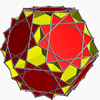 U63 Great dodecicosahedron In geometry, the great dodecicosahedron is a nonconvex uniform polyhedron, indexed as U63. Its vertex figure is a crossed quadrilateral.It has a composite Wythoff symbol, 3 5/3 |, requiring two different Schwarz triangles to generate it: and .Its vertex figure 6.10/3.6/5.10/7 is also ambiguous,... |
||||||
 Nonuniform truncated dodecahedron |
 U72 Small retrosnub icosicosidodecahedron In geometry, the small retrosnub icosicosidodecahedron is a nonconvex uniform polyhedron, indexed as U72.- Convex hull :Its convex hull is a nonuniform truncated dodecahedron.- Cartesian coordinates :... |
|||||||
 Dodecahedron |
 {5/2,3} |
 U30 Small ditrigonal icosidodecahedron In geometry, the small ditrigonal icosidodecahedron is a nonconvex uniform polyhedron, indexed as U30.-Related polyhedra:Its convex hull is a regular dodecahedron... |
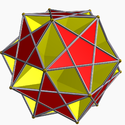 U41 Ditrigonal dodecadodecahedron In geometry, the Ditrigonal dodecadodecahedron is a nonconvex uniform polyhedron, indexed as U41.- Related polyhedra :Its convex hull is a regular dodecahedron... |
 U47 |
||||
 Rhombicosidodecahedron Rhombicosidodecahedron In geometry, the rhombicosidodecahedron, or small rhombicosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed of two or more types of regular polygon faces.... |
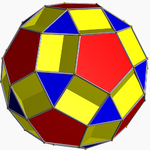 U33 Small dodecicosidodecahedron In geometry, the small dodecicosidodecahedron is a nonconvex uniform polyhedron, indexed as U33. Its vertex figure is a crossed quadrilateral.-Related polyhedra:... |
 U39 Small rhombidodecahedron In geometry, the small rhombidodecahedron is a nonconvex uniform polyhedron, indexed as U39. Its vertex figure is a crossed quadrilateral.- Related polyhedra :... |
 U58 |
|||||
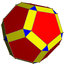 Beveled Dodecahedron |
 U55 |
|||||||
 Nonuniform rhombicosidodecahedron |
 U31 Small icosicosidodecahedron In geometry, the small icosicosidodecahedron is a nonconvex uniform polyhedron, indexed as U31.- Related polyhedra :It shares its vertex arrangement with the great stellated truncated dodecahedron... |
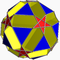 U43 Small ditrigonal dodecicosidodecahedron In geometry, the small ditrigonal dodecicosidodecahedron is a nonconvex uniform polyhedron, indexed as U43. Its vertex figure is a crossed quadrilateral.- Related polyhedra :It shares its vertex arrangement with the great stellated truncated dodecahedron... |
 U50 Small dodecicosahedron In geometry, the small dodecicosahedron is a nonconvex uniform polyhedron, indexed as U50. Its vertex figure is a crossed quadrilateral.-Related polyhedra:It shares its vertex arrangement with the great stellated truncated dodecahedron... |
 U66 |
||||
 Nonuniform rhombicosidodecahedron |
 U75 Great dirhombicosidodecahedron In geometry, the great dirhombicosidodecahedron is a nonconvex uniform polyhedron, indexed last as U75.This is the only uniform polyhedron with more than six faces meeting at a vertex... |
 U64 Great snub dodecicosidodecahedron In geometry, the great snub dodecicosidodecahedron is a nonconvex uniform polyhedron, indexed as U64.- Related polyhedra :It shares its vertices and edges, as well as 20 of its triangular faces and all its pentagrammic faces, with the great dirhombicosidodecahedron,... |
 Skilling's figure Great disnub dirhombidodecahedron In geometry, the great disnub dirhombidodecahedron, also called Skilling's figure, is a uniform star polyhedron.John Skilling discovered this one further uniform polyhedron, by relaxing the condition that only two faces may meet at an edge... (see below) |
|||||
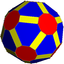 Nonuniform truncated icosidodecahedron Truncated icosidodecahedron In geometry, the truncated icosidodecahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces.... |
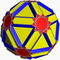 U45 Icositruncated dodecadodecahedron In geometry, the icositruncated dodecadodecahedron is a nonconvex uniform polyhedron, indexed as U45.- Convex hull :Its convex hull is a nonuniform great rhombicosidodecahedron.- Cartesian coordinates :... |
|||||||
 Nonuniform truncated icosidodecahedron Truncated icosidodecahedron In geometry, the truncated icosidodecahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces.... |
 U59 |
|||||||
 Nonuniform truncated icosidodecahedron Truncated icosidodecahedron In geometry, the truncated icosidodecahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces.... |
 U68 |
|||||||
 Nonuniform snub dodecahedron Snub dodecahedron In geometry, the snub dodecahedron, or snub icosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces.... |
 U40 |
 U46 Snub icosidodecadodecahedron In geometry, the snub icosidodecadodecahedron is a nonconvex uniform polyhedron, indexed as U46.- Cartesian coordinates :Cartesian coordinates for the vertices of a snub icosidodecadodecahedron are all the even permutations of... |
 U57 |
 U69 |
 U60 |
 U74 |
Skilling's figure
One further nonconvex polyhedron is the Great disnub dirhombidodecahedronGreat disnub dirhombidodecahedron
In geometry, the great disnub dirhombidodecahedron, also called Skilling's figure, is a uniform star polyhedron.John Skilling discovered this one further uniform polyhedron, by relaxing the condition that only two faces may meet at an edge...
, also known as Skilling's figure, which is vertex-uniform, but has pairs of edges which coincide in space such that four faces meet at some edges.
It is sometimes but not always counted as a uniform polyhedron. It has Ih symmetry.

Degenerate cases
Coxeter identified a number of degenerate star polyhedra by the Wythoff construction method, which contain overlapping edges or vertices. These degenerate forms include:- Small complex icosidodecahedron
- Great complex icosidodecahedron

