
Small snub icosicosidodecahedron
Encyclopedia
In geometry
, the small snub icosicosidodecahedron is a uniform star polyhedron, indexed as U32. It has 112 faces (100 triangle
s and 12 pentagram
s), 180 edges, and 60 vertices.
is a nonuniform truncated icosahedron
.
where τ = (1+√5)/2 is the golden ratio
(sometimes written φ).
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the small snub icosicosidodecahedron is a uniform star polyhedron, indexed as U32. It has 112 faces (100 triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
s and 12 pentagram
Pentagram
A pentagram is the shape of a five-pointed star drawn with five straight strokes...
s), 180 edges, and 60 vertices.
Convex hull
Its convex hullConvex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
is a nonuniform truncated icosahedron
Truncated icosahedron
In geometry, the truncated icosahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids whose faces are two or more types of regular polygons.It has 12 regular pentagonal faces, 20 regular hexagonal faces, 60 vertices and 90 edges....
.
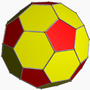 Truncated icosahedron (regular Regular polygon A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:... faces) |
 Convex hull (isogonal hexagons) |
 Small snub icosicosidodecahedron |
Cartesian coordinates
Cartesian coordinates for the vertices of a small snub icosicosidodecahedron are all the even permutations of- (±½(−1/τ+√(3τ−2)), 0, ±½(3+τ√(3τ−2)))
- (±½(1/τ+√(3τ−2)), ±1, ±½(1+2/τ+τ√(3τ−2)))
- (±½(τ2+√(3τ−2)), ±1/τ, ±½(1+τ√(3τ−2)))
where τ = (1+√5)/2 is the golden ratio
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
(sometimes written φ).

