Vertex arrangement

In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, a vertex arrangement is a set of points in space described by their relative positions. They can be described by their use in polytope

Polytope

In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...

s.

For example a square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...

vertex arrangement is understood to mean four points in a plane, equal distance and angles from a center point.

Two polytopes share the same vertex arrangement if they share the same 0-skeleton

N-skeleton

In mathematics, particularly in algebraic topology, the n-skeleton of a topological space X presented as a simplicial complex refers to the subspace Xn that is the union of the simplices of X of dimensions m ≤ n...

The same set of vertices can be connected by edges in different ways. For example the pentagon and pentagram have the same vertex arrangement, while the second connects alternate vertices.

Two polygons with same *vertex arrangement*.
pentagon Pentagon In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...	pentagram Pentagram A pentagram is the shape of a five-pointed star drawn with five straight strokes...

A vertex arrangement is often described by the convex hull

Convex hull

In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....

polytope which contains it. For example, the regular pentagram can be said to have a (regular) pentagonal vertex arrangement.

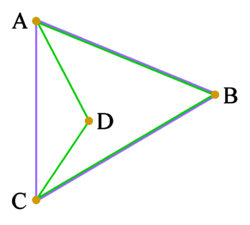	ABCD is a concave quadrilateral Quadrilateral In Euclidean plane geometry, a quadrilateral is a polygon with four sides and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon , hexagon and so on... (green). Its vertex arrangement is the set {A, B, C, D}. Its convex hull is the triangle Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... ABC (blue). The vertex arrangement of the convex hull is the set {A, B, C}, which is not the same as that of the quadrilateral; so here, the convex hull is not a way to describe the vertex arrangement.

Infinite tilings can also share common vertex arrangements.

For example, this triangular lattice of points can be connected to form either isosceles triangles or rhombic

Rhombus

In Euclidean geometry, a rhombus or rhomb is a convex quadrilateral whose four sides all have the same length. The rhombus is often called a diamond, after the diamonds suit in playing cards, or a lozenge, though the latter sometimes refers specifically to a rhombus with a 45° angle.Every...

faces.

Four tiling
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...

s with same *vertex arrangement*.
Lattice points	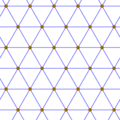Triangular tiling	rhombic Rhombus In Euclidean geometry, a rhombus or rhomb is a convex quadrilateral whose four sides all have the same length. The rhombus is often called a diamond, after the diamonds suit in playing cards, or a lozenge, though the latter sometimes refers specifically to a rhombus with a 45° angle.Every... tiling	Zig-zag rhombic tiling	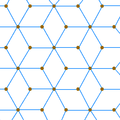Rhombille tiling

Edge arrangement

Polyhedra

Polyhedron

In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...

can also have the same edge arrangement which means they have similar vertex and edge arrangements, but may differ in their faces.

For example the self-intersecting great dodecahedron shares it edge arrangement with the convex icosahedron.

Two polyhedra with same *edge arrangement*.
icosahedron Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... (20 triangles)	great dodecahedron (12 intersecting pentagons)

Face arrangement

4-polytopes

Polychoron

In geometry, a polychoron or 4-polytope is a four-dimensional polytope. It is a connected and closed figure, composed of lower dimensional polytopal elements: vertices, edges, faces , and cells...

can also have the same face arrangement which means they have similar vertex, edge, and face arrangements, but may differ in their cells.

For example, of the ten nonconvex regular Schläfli-Hess polychora, there are only 7 unique face arrangements.

For example the grand stellated 120-cell and great stellated 120-cell, both with pentagram

Pentagram

A pentagram is the shape of a five-pointed star drawn with five straight strokes...

mic faces, appear visually indistinguishable without a representation of their cells

Cell (geometry)

In geometry, a cell is a three-dimensional element that is part of a higher-dimensional object.- In polytopes :A cell is a three-dimensional polyhedron element that is part of the boundary of a higher-dimensional polytope, such as a polychoron or honeycomb For example, a cubic honeycomb is made...

Two (projected) polychora with same *face arrangement*
Grand stellated 120-cell (120 small stellated dodecahedrons)	Great stellated 120-cell (120 great stellated dodecahedrons)

Classes of similar polytopes

George Olshevsky

George Olshevsky is a freelance editor, writer, publisher, amateur paleontologist, and mathematician living in San Diego, California.Olshevsky maintains the comprehensive online Dinosaur Genera List...

advocates the term army for a class of polytopes that share an element arrangement. More generally he defines n-regiments for polytopes that share elements up to dimension n. So a regiment (1-regiment) shares the same edge and vertex arrangement. He called a set of polytopes with the same 2-regiment as a company.

External links

(Same vertex arrangement) (Same vertex and edge arrangement) (Same vertex, edge and face arrangement)

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.