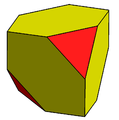
Truncated cube
Encyclopedia
In geometry
, the truncated cube, or truncated hexahedron, is an Archimedean solid
. It has 14 regular faces (6 octagonal and 8 triangular), 36 edges, and 24 vertices.
If the truncated cube has unit edge length, its dual triakis octahedron
has edges of lengths 2 and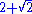 .
.
V of a truncated cube of edge length a are: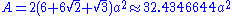
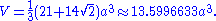
The following Cartesian coordinates define the vertices of a truncated
hexahedron
centered at the origin with edge length 2ξ:
where ξ =
with its corners truncated
, as shown in this truncation sequence:
It shares the vertex arrangement
with three nonconvex uniform polyhedra
:
A cube can be alternately truncated producing tetrahedral symmetry
, with 6 hexagonal faces, and 4 triangles at the truncated vertices.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the truncated cube, or truncated hexahedron, is an Archimedean solid
Archimedean solid
In geometry an Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices...
. It has 14 regular faces (6 octagonal and 8 triangular), 36 edges, and 24 vertices.
If the truncated cube has unit edge length, its dual triakis octahedron
Triakis octahedron
In geometry, a triakis octahedron is an Archimedean dual solid, or a Catalan solid. Its dual is the truncated cube.It can be seen as an octahedron with triangular pyramids added to each face; that is, it is the Kleetope of the octahedron. It is also sometimes called a trisoctahedron, or, more...
has edges of lengths 2 and
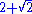 .
.Area and volume
The area A and the volumeVolume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
V of a truncated cube of edge length a are:
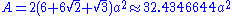
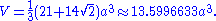
Cartesian coordinates
The following Cartesian coordinates define the vertices of a truncated
Truncation (geometry)
In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :...
hexahedron
Hexahedron
A hexahedron is any polyhedron with six faces, although usually implies the cube as a regular hexahedron with all its faces square, and three squares around each vertex....
centered at the origin with edge length 2ξ:
- (±ξ, ±1, ±1),
- (±1, ±ξ, ±1),
- (±1, ±1, ±ξ)
where ξ =

Related polyhedra
The truncated cube can be seen as a cubeCube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
with its corners truncated
Truncation (geometry)
In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :...
, as shown in this truncation sequence:
 Cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
 Truncated cube |
 cuboctahedron Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... |
 Truncated octahedron Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron.... |
 Octahedron Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
It shares the vertex arrangement
Vertex arrangement
In geometry, a vertex arrangement is a set of points in space described by their relative positions. They can be described by their use in polytopes....
with three nonconvex uniform polyhedra
Nonconvex uniform polyhedron
In geometry, a uniform star polyhedron is a self-intersecting uniform polyhedron. They are also sometimes called nonconvex polyhedra to imply self-intersecting...
:
 Truncated cube |
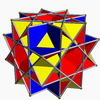 Nonconvex great rhombicuboctahedron |
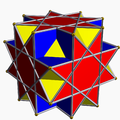 Great cubicuboctahedron Great cubicuboctahedron In geometry, the great cubicuboctahedron is a nonconvex uniform polyhedron, indexed as U14.- Related polyhedra :It shares the vertex arrangement with the convex truncated cube and two other nonconvex uniform polyhedra... |
 Great rhombihexahedron Great rhombihexahedron In geometry, the great rhombihexahedron is a nonconvex uniform polyhedron, indexed as U21. Its dual is the great rhombihexacron. Its vertex figure is a crossed quadrilateral.- Related polyhedra :... |
A cube can be alternately truncated producing tetrahedral symmetry
Tetrahedral symmetry
150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
, with 6 hexagonal faces, and 4 triangles at the truncated vertices.
See also
- Spinning truncated cube
- Cube-connected cyclesCube-connected cyclesIn graph theory, the cube-connected cycles is an undirected cubic graph, formed by replacing each vertex of a hypercube graph by a cycle. It was introduced by for use as a network topology in parallel computing.- Definition :...
, a family of graphs that includes the skeleton of the truncated cube
External links
- Editable printable net of a truncated cube with interactive 3D view
- The Uniform Polyhedra
- Virtual Reality Polyhedra www.georgehart.com: The Encyclopedia of Polyhedra
- VRMLVRMLVRML is a standard file format for representing 3-dimensional interactive vector graphics, designed particularly with the World Wide Web in mind...
model - Conway Notation for Polyhedra Try: "tC"
- VRML